膨胀式尾管悬挂器用膨胀管受力分析

刘 凤，罗西超，王瑞霄，周家齐

（北京石油机械厂，北京100083） ①

根据式（8）、（10）～（12）、（15）可以确定膨胀力的大小。

1.5 膨胀管回弹计算

膨胀管材料的性能曲线如图4，根据冷作硬化原理，在等效应力σeqv的作用下，材料达到ε1的变形。当应力撤去以后，材料将回弹到ε2，则材料的回弹应变为

膨胀式尾管悬挂器用膨胀管受力分析

刘 凤，罗西超，王瑞霄，周家齐

（北京石油机械厂，北京100083）①

膨胀式尾管悬挂器是一种新型的尾管固井、完井工具，其工作的核心构件是膨胀管，膨胀管的膨胀性能是悬挂、坐封成功的关键。对膨胀管的膨胀力及膨胀后的外径比理论外径缩小量进行了分析，并探讨了一种理论计算方法，为膨胀管材料的选择、结构的设计提供了一定理论依据。

膨胀式尾管；悬挂器；膨胀管；膨胀力

在膨胀管技术基础上发展起来的膨胀式尾管悬挂器凭借着可旋转固井、密封能力强、坐封后内通径大等优点得到了推广和应用［1］。

膨胀式尾管悬挂器的核心是利用实体膨胀管的金属塑性应变特性，通过对可膨胀本体进行径向膨胀，使悬挂器本体膨胀至塑性变形区域，发生永久变形。

膨胀式尾管悬挂器的悬挂机构如图1，主要包括膨胀锥和膨胀管2个核心组件。

图1 膨胀式尾管悬挂器悬挂机构

当尾管悬挂器被膨胀时，膨胀锥受液压力作用沿中心管滑行，扩涨膨胀管，将膨胀管外的橡胶带和环形肋挤压到套管上，使其紧贴到套管内壁上并在贴合面上产生巨大的摩擦力来承受轴向载荷，同时在贴合面上形成高效密封。

膨胀管及膨胀锥的设计计算主要需要考虑膨胀力、坐挂力、密封性能等因素。

1 膨胀力及回弹计算

1.1 宏观受力

膨胀管膨胀过程是在膨胀锥上作用轴向载荷，膨胀锥在载荷作用下轴向移动，使膨胀管产生环向膨胀变形，当膨胀管上的等效应力达到材料的屈服极限时，变形就是永久变形。膨胀管在膨胀过程分为如图2所示的3个部分。L1是未膨胀部分；L2是扩孔部分，在此段膨胀过程膨胀管先发生弹性形变，随着压力进一步增加及膨胀锥的推进，膨胀管达至弹性极限状态，继而，膨胀管的形变进入塑性区，产生永久变形；L3段为已膨胀段，不再产生大变形，扩管体进行局部修圆［2－3］。

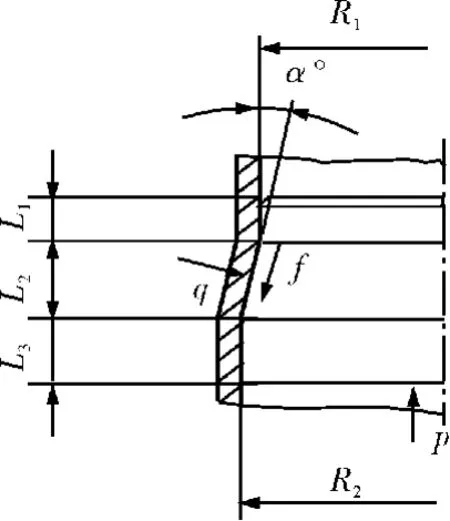
图2 膨胀管膨胀过程

1.2 弹性区域力学分析

膨胀管的变形处于弹性区域时，膨胀锥挤压膨胀管是一个弹塑性变形的过程。首先在压力作用下，膨胀管发生弹性变形，随着压力进一步增加，膨胀管达到弹性极限状态，由拉梅公式［4－5］可得径向应力为

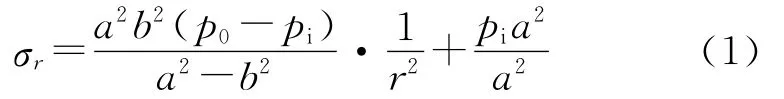
周向应力为

1.3 塑性压力分析

膨胀管在进入塑性变形区域时，其应力状态比较复杂，但在该边界区域内等效应力必然达到了屈服条件。特别是该区域的范围特别微小，可以忽略，所以在分析膨胀区域应力状态和变形时，通常取该区域以外的其他点作为分析研究对象［6］。

为了方便分析问题，在选取单元体时按主应力方向选主应力微单元，通过分析主应力与屈服应力的关系建立理论载荷的分析方法。围绕膨胀区域任一点取1个微元体段，如图3。该膨胀管膨胀区微

式中，p0为外压，MPa；pi为内压，MPa；a为管子内半径，mm；b为管子外半径，mm；r为微元体半径，mm。

在没有完全膨胀时忽略外压（即p0＝0），当膨胀管处于弹性极限状态时（即pi＝pe），根据第三强度理论，在r＝a处的应力pe应满足单元选取如下：垂直于锥面相距dl的2个平面，过圆锥中心线成dθ的2个平面以及内、外圆锥面6个面围成的微单元为主应力单元体，平行于轴线的两平面夹角为dβ，膨胀锥的锥角为α，r为微元体半径，t为膨胀管壁厚，q为微元体锥面内压力，

图3 膨胀管膨胀段微小单元受力分析

其中

由图3，微元体在锥面方向上的平衡方程为

将式（5）～（7）带入式（4）并省略三阶无穷小项，得

微元体在垂直于锥面上的平衡方程为

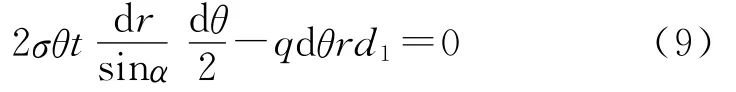
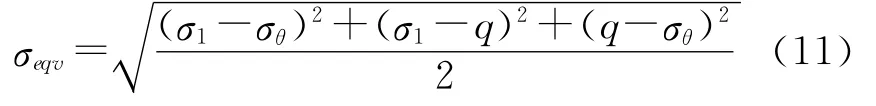
假设膨胀管膨胀过程是稳定的、匀速的，则膨胀过程中

式中，σs为膨胀管材料的许用屈服强度。

1.4 膨胀力

如图2，膨胀锥受内压p，锥面上有压力q及摩擦力f。假设膨胀锥运动过程是稳定的、匀速的，则膨胀锥轴向受力为

取σθ、σ1、q为主应力。根据Mises屈服准则，此微单元的等效应力为

将式（5）带入式（9）并省略三阶无穷小项，得

根据式（8）、（10）～（12）、（15）可以确定膨胀力的大小。

1.5 膨胀管回弹计算

膨胀管材料的性能曲线如图4，根据冷作硬化原理，在等效应力σeqv的作用下，材料达到ε1的变形。当应力撤去以后，材料将回弹到ε2，则材料的回弹应变为

式中，R1为膨胀管变形前内径，mm；R2为变形后内径，mm。

径向受力为

根据式（13）～（14）计算得

图4 材料应力应变曲线

当变形到R2时，变形最大，根据式（11）计算出此时的σeqv。膨胀管变形量为

则回弹量为

1.6 膨胀后外径计算

膨胀管膨胀过程中可视为体积不变，膨胀管膨胀后壁厚和长度会有所变化，假设长度外径比＞10，忽略长度方向的变化，则截面积变化量相等，即

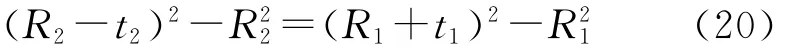
金属材料的弹性模量为E，则

式中，t1为膨胀前壁厚，mm；t2为膨胀后壁厚，mm。则壁厚变化量为

解式（20）及（21）得

则膨胀后的外径比理论外径缩小量为

2 实际应用

通过以上计算方法，能够优化膨胀锥的膨胀角，预先确定理论需要的膨胀压力。由中国石油集团钻井工程技术研究院机械所设计、北京石油机械厂制造的新型膨胀式尾管悬挂器在哈萨克NB1058－2H井获得成功应用。该膨胀管膨胀材料屈服强度σs＝320 MPa，σb＝510MPa，弹性模量E＝200GPa，摩擦因数取为0.25，膨胀管膨胀前管子内径R1＝60mm，膨胀后管子内径R2＝65mm，膨胀锥角为8.9°。经过计算等效应力σeqv＝306MPa，膨胀力为21.2MPa，膨胀后外径比理论外径缩小2（Δt＋Δ）＝0.35mm。通过4次膨胀试验，确定膨胀力为25～28MPa，膨胀后的外径比理论缩小量为0.45mm。

理论计算的膨胀力偏差小于15%，回弹量偏差小于15%，对于实践有一定的指导意义。

3 结论

1） 膨胀式尾管悬挂器的膨胀管膨胀后直径决定了其坐封的效果及悬挂力的大小。

2） 探索了一种膨胀管膨胀后的外径比理论缩小量的计算方法，经过实践证明，具有一定的指导意义，在此基础上还可以继续探讨更精确的计算方法。

［1］ 彭在美，赵 旭.国内外可膨胀套管技术的发展概况［J］.焊管，2010，33（6）：5－9.

［2］ 姜 伟.膨胀管弹塑性力学特性分析与设计研究［J］.中国海上油气，2008，20（2）：111－114.

［3］ 梁 坤，练章华，任荣坤，等.实体膨胀管膨胀力影响因素数值模拟［J］.石油矿场机械，2010，39（12）：1－4.

［4］ 秦国明，何东升，张丽平，等.基于ANSYS／LS2DYNA的实体膨胀管膨胀力分析［J］.石油矿场机械，2009，38（8）：9－12.

［5］ 王仲仁，苑世剑，胡连喜.弹性与塑性力学基础［M］.哈尔滨：哈尔滨工业大学出版社，1997.

［6］ 张 建，肖 刚，孙 骞，等.实体膨胀管膨胀过程数值模拟及结构优化［J］.石油矿场机械，2011，40（5）：67－70.

Force Analysis of Expandable Tube for Expandable Liner Hanger

L
IU Feng，LUO Xi－chao，WANG Rui－xiao，ZHOU Jia－qi
（Beijing Petroleum Machinery Plant，Beijing100083，China）

Expanding drilling liner hanger is a new type of tool for liner cementing and well completion，bulged tube is the core component part of the expanding drilling liner hanger，the expandability of the bulged tube is the key of successful hanging and setting.The bulging force of the bulged tube was analyzed in this dissertation；a theory method to compute the reduction of the actual OD was probed after expanding compared with the theory OD，which can offer theory reference for material selecting and structural design of the bulged tube.

expanding drilling；liner hanger；bulged tube；bulging force

1001－3482（2012）01－0030－03

TE925.2

A

2011－08－01

刘 凤（1978－），女，辽宁辽阳人，硕士，2004年毕业于中国石油大学机械设计及理论专业，主要从事膨胀式尾管悬挂器的设计工作，E－mail：liufengdri＠cnpc.com.cn。