基于小波熵与相关性相结合的小波模极大值地震信号去噪

李 文 刘 霞 段玉波 姚建红 刘继承 潘洪屏

（中国黑龙江大庆163318东北石油大学）

基于小波熵与相关性相结合的小波模极大值地震信号去噪

李 文 刘 霞 段玉波 姚建红 刘继承 潘洪屏

（中国黑龙江大庆163318东北石油大学）

小波模极大值去噪算法中将高频小波系数全部当做噪声处理，忽略了高频小波系数中仍含有的有用信息，从而导致了模极大值传播点错选现象以及计算出的噪声方差中仍含有用信息.针对这些问题，提出了小波熵与相关性相结合的小波模极大值去噪算法.将高频小波系数进行相关处理，确定有效信号的位置；将最大尺度上的高频小波系数划分成若干个小区间，计算各区间小波熵；以小波熵最大区间的高频小波系数的平均值作为噪声方差，根据Donoho提出的阈值公式计算最大尺度上的阈值；经阈值比较得到的模极大值点位置与相关处理得到的有用信息的位置进行比较，保留相同位置的模极大值，剔除位置不同由噪声引起的模极大值点；采用即兴（Adhoc）算法逐级搜索各尺度上的模极大值，并用交替投影算法进行重构.该算法实现了阈值的自适应选取，并有效解决了去除错选模极大值传播点的问题.将本算法和传统去噪方法用于仿真信号处理中，经对比分析验证了本算法的有效性.

模极大值 小波熵 相关性 地震信号 去噪

引言

从野外采集的地震信号中通常叠加了各种干扰信息，不宜直接应用于地质解释（王秀明，2007）.因此，提取地震信号中的有用信息，提高地震资料的信噪比，一直是地震信号处理的首要问题.由于近地表的衰减和岩石的吸收、透射损失、散射等多种作用，由震源激发的子波在穿过地下介质后，在不同传播时间处子波的振幅、频率都有不同的特征（陆基孟，2005）.因此地震信号属于非平稳信号.傅里叶变换等传统去噪方法在处理非平稳信号中存在着不足（姜弢等，2002；孔祥茜等，2005）.小波变换在时域和频域都具有良好的局部化性质，是分析非平稳信号的强有力工具（Hsung，Lun，1999；Ykhlef，Arezki，2004）.近年来，人们将小波变换方法应用于地震信号去噪领域，取得了较好的效果（李华，2000；田金文等，2001；张媛玲，2001；周怀来，2006；朱晓明，2007）.Witkin（1983）首先提出了利用空间相关去噪的思想.Mallat和Zhong（1992）提出利用小波系数的局部极大值点重构信号进行去噪的方法.陈德智等（1998）和孙丰荣等（2005）研究了小波模极大值快速重构算法.该算法对小波分解后的系数直接求出模极大值，在去除最大尺度上的噪声对应的模极大值点时一般根据经验选取阈值，并且在搜索模极大值传播点时容易出现错选现象（姚胜利，2007；潘洪屏，2011）.针对这些问题，本文提出了小波熵与相关性相结合的小波模极大值去噪算法.该算法可根据信号的能量特征自适应地选取阈值，并有效解决了去除错选模极大值传播点的问题.

1 小波模极大值去噪算法

1.1 信号在小波变换下的特性

根据信号f（t）奇异性与李氏指数（Lipschitz exponent）的关系，有信号f（t）的小波变换模极大值

式中，j为二进尺度参数，t取离散值.由式（1）可得

由式（2）可以看出，若李氏指数α＞0，则随着尺度j的增加，小波变换模极大值的对数也变大；若李氏指数α＜0，则小波变换后系数的模极大值随着尺度的增加反而减小，表明信号比不连续的情况（且有界，李氏指数α＝0）更加奇异，噪声就属于这种情况.实际地震记录中的反射波是连续而且可导的，不连续点的值也是有限的，因此可以确定该点的李氏指数α值满足α≥0.所以，有效信号的小波变换模极大值是随着尺度的增加而增大的.而白噪声具有负的李氏指数α＝－（1／2）－ε，∀ε＞0，它的小波变换模极大值是随着尺度的增大而减小的.因此，根据小波变换模极大值的变化特性来检测信号的局部奇异性，通过搜寻尺度空间中的模极大值曲线，并利用信号和噪声在各个尺度下的不同特性，可以实现信号的去噪（徐长发，李国宽，2004；蒋鹏，2004；段炜，2008）.

1.2 小波变换模极大值去噪算法

该算法的基本思想是根据信号的模极大值随尺度的增加而增大，而噪声的模极大值随尺度的增加而减小的特性，去除小于阈值的由噪声引起的模极大值，保留由有效信号引起的模极大值点，然后用保留的模极大值重构信号.算法步骤如下：

1）对含噪信号进行多尺度小波分解，得到低频小波系数（近似系数）和高频小波系数（细节系数），计算各尺度上细节系数的模极大值.分解尺度以3—5为宜.

2）选取最大尺度上的阈值.其方法为：根据噪声设置一个阈值，保留大于该阈值的最大尺度（设为4）上的模极大值点，若小于该阈值的模极大值点则剔除.

3）在尺度j－1上寻找尺度j（3≤j≤J）上小波变换模极大值点的传播点，即去掉尺度j－1上噪声的模极大值点，保留有效信号的模极大值点.在搜索过程中可以采用Adhoc算法搜索哪些模极大值点传播到下一尺度.其方法为：在尺度j上的模极大值点的位置，构造一个邻域o（nji，εj）.其中nji为尺度j的第i个极值点，εj为仅与尺度j有关的常数.在尺度j－1上剔除落在邻域o（nji，εj）外的模极大值点，保留落在邻域o（nji，εj）内的模极大值点，将其作为尺度j－1上的有效模极大值点.令j＝j－1，逐尺度搜索直到j＝2.

4）考虑到尺度j＝1时的信号几乎由噪声控制，所以将尺度j＝1上的小波变换模极大值点全部去掉.

5）根据保留下来的每一尺度上新的模极大值点对应的模极大值，选择重构算法来重构信号.

可见，最大尺度上阈值的选取是该算法的关键.通常阈值选取公式为T＝｛max［Wd2j f（ki）］｝／J，但它有几个缺点：① 若信号给定，则T基本固定，这样不能体现出信号与噪声的关系；②若T偏大，则有效信号损失较多；③若T偏小，则会含有许多残留噪声.将噪声的模极大值点作为有效信号的模极大值点保留下来，导致去噪后的信号中仍含有噪声.因此，在搜索过程中会出现由有效信号产生的模极大值的传播点错选现象.本文针对阈值选取问题提出了改进算法 小波熵与相关性相结合的小波模极大值去噪算法.

2 基于小波熵与相关性相结合的小波模极大值去噪算法

2.1 改进算法的基本思想

为避免在搜索模极大值传播点时出现错选现象，我们采用以下步骤：①对信号的各尺度细节系数进行相关处理，确定出有效信号的位置，并存储该有效信号的位置；② 确定最大尺度上的阈值：将最大尺度上的细节系数分成若干小区间，计算各区间的小波熵，将小波熵最大区间的细节系数的平均值作为噪声方差，计算出最大尺度上的阈值；③ 搜索各尺度上的模极大值点：先确定最大尺度上的模极大值，将其与阈值比较，为了确定出大于阈值的模极大值点是否由有效信号引起，将这些模极大值点与相关处理得到的有效信号的位置进行比较，位置相同的即由有效信号引起，因此保留下来，位置不同的则由噪声引起，将其剔除，从而得到最大尺度上的有效模极大值点；④根据Adhoc算法逐尺度搜索，每一尺度搜索得到的模极大值点位置都要与该尺度相关处理存储的有效位置进行比较，确定该尺度有效模极大值点；⑤ 利用交替投影法对各尺度上的有效模极大值进行重构，得到去噪后的信号.

2.2 各尺度间的相关性计算方法

由于有效信号的小波系数在各尺度间具有较强的相关性，而噪声的小波系数在各尺度间无明显相关性，根据这一特性可提取有效信号和噪声.对含噪信号进行小波分解后得到低频小波系数和高频小波系数.高频小波系数中可能含有有效信号，在去除噪声时，需保留，避免造成有效信号的损失.若不进行相关处理，去噪时会损失有效信号的频率成分，使信号频带变窄而造成分辨率下降.因此，在去噪时需要将这些有效信号和信号突变点处的信号保留下来.

首先定义相关系数.将c（j，k）称为分解尺度j上k点的相关系数，Wf（j，k）和Wf（j＋1，k）分别为尺度j和尺度j＋1上k点的小波系数，则有

为使相关系数与小波系数具有可比性（孙延奎，2005），需要定义规范化（normalization）相关系数.定义式（4）为c（j，k）的规范化相关系数

其中

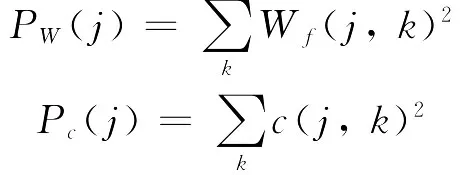
2.3 小波熵的计算方法

当小波基函数是一组正交基时，小波变换能量守恒，即

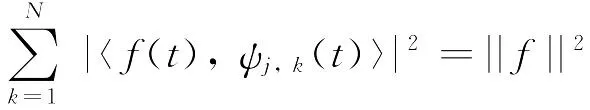
从而可以定义单一尺度下的小波能量为该尺度小波系数的平方和

由此可得，信号的总能量表达式为

其中，第j层的细节系数为djk，采样点数为N，将采样点上的细节系数等分成n个小区间，每个小区间有N／n个采样点，则第i个子区间的细节系数对应的能量为

第j层细节系数的总能量为

第i个子区间的信号能量在该尺度总能量下的概率为

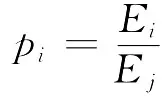
则第i个子区间小波熵定义（Alnashash，Paul，2003；He，Cai，2004；张荣标等，2007）为

2.4 阈值的计算

计算各尺度的小波熵.将熵值最大子区间的细节系数的平均值作为各尺度上的噪声方差.根据Donoho（1995）提出的阈值公式计算各尺度阈值，则尺度j上的阈值为

式中，σj为尺度j上的噪声方差.这样计算出的阈值能根据信号自身的能量特征自适应地确定各尺度上的阈值.

2.5 小波熵与相关性相结合的小波模极大值去噪算法

该方法具体步骤为：① 对含噪信号进行多尺度小波分解，得到低频小波系数（近似系数）和高频小波系数（细节系数）；② 对细节系数进行相关性处理，将相邻两尺度的细节系数相乘得到各尺度上的相关系数，再利用各尺度上的相关系数和细节系数，根据式（3）和式（4）计算出各尺度上的规范化相关系数，并将规范化相关系数与细节系数进行比较，把各尺度上规范化相关系数大于细节系数的位置记录下来并储存；③ 求出步骤①中分解得到的各尺度上细节系数的模极大值，得到模极大值和对应的模极大值点；④ 根据式（5）计算各尺度、各区间小波熵，将各区间小波熵最大子区间的细节系数的平均值作为各尺度的噪声方差，根据式（6）计算最大尺度J上的阈值，若步骤③中计算的最大尺度的模极大值大于该阈值，则保留该模极大值点，否则予以剔除，由此得到最大尺度J上的有效模极大值点；⑤将步骤④中得到新的模极大值点的位置与步骤②中储存的最大尺度J上记录下来的位置相比较，若新的模极大值点与记录下来的对应位置相同，则保留该模极大值点，否则去除，比较后又得到最大尺度上新的模极大值点；⑥在尺度j－1（第3尺度）上寻找尺度j（第4尺度）上小波变换模极大值点的传播点，可以用Adhoc算法来搜索哪些模极大值点传播到下一尺度.对于尺度j－1上的一个模极大值a，若它与尺度j上的一个模极大值b有相同的符号，位置也比较接近且有较大的幅值，就称a为b的传播点.具体做法是在尺度j上的模极大值点的位置，构造一个邻域o（nji，εj），其中nji为尺度j的第i个模极大值点，εj为仅与尺度j有关的常数，在尺度j－1上剔除落在邻域o（nji，εj）外的模极大值点，保留落在邻域o（nji，εj）内的模极大值点，得到尺度j－1上的有效模极大值点，然后将有效模极大值点与步骤②中储存的尺度j－1上记录下来的位置数据相比较，即重复步骤⑤，从而又得到尺度j－1上的有效模极大值点；⑦ 令j＝j－1，重复步骤⑥，这样逐级搜索，逐级比较，直到j＝2为止，最后对尺度j＝1，保留与j＝2上模极大值点位置相同的模极大值点，其余位置上的模极大值置为零，然后与步骤②中相关处理存储的尺度j＝1的位置比较，去掉对应位置上不相同的模极大值点，得到尺度j＝1上有效模极大值点；⑧根据各个尺度上的有效模极大值点得到对应的各个尺度上的模极大值，利用交替投影法重构信号.

图3 巴特沃斯（Butterworth）与切比雪夫（Chebyshev）Ⅰ型去噪对比（a）Butterworth滤波器去噪图；（b）Butterworth去噪结果与原信号残差图；（c）ChebyshevⅠ型滤波器去噪图；（d）ChebyshevⅠ型去噪结果与原信号残差图Fig.3 Comparison between Butterworth and ChebyshevⅠdenoising filters（a）Butterworth；（b）Residuals between Butterworth result and original signal；（c）ChebyshevⅠ；（d）Residuals between result of ChebyshevⅠand original signal

3 仿真

3.1 对含噪的Ricker子波进行去噪处理

图1为Ricker子波、噪声和加噪的Ricker子波图；图2为采用FIR滤波器去噪对比图；图3为采用IIR滤波器去噪对比图；图4为改进去噪算法与小波变换模极大值去噪波形图.两种算法均选取sym8小波，阈值函数均采用软阈值函数，分解尺度均为4.表1示出几种算法的均方误差及信噪比.

从图2—4中可以看出，几种算法都基本抑制了噪声，但是FIR滤波器、IIR滤波器和小波变换模极大值去噪后的波形与原信号相差较大，在许多点上波形发生了变形，有效信号有所损失，去噪后的信号不够光滑.而改进的模极大值去噪算法与原信号相差不大，有效信号得到了很好的保留，去噪后信号较光滑.从信噪比和均方误差来看，改进算法的信噪比高于其它算法，均方误差小于其它算法，说明改进的模极大值去噪算法具有很好的去噪效果，基本不损失有效信号.

图4 改进算法与模极大值去噪对比.（a）改进算法去噪图；（b）改进算法去噪结果与原信号残差图；（c）模极大值去噪图；（d）模极大值去噪结果与原信号残差图Fig.4 Comparison between denoised results of the improved algorithm and modulus maxima algorithm.（a）Result of the improved algorithm result；（b）Residuals between results of the improved algorithm and original signal；（c）Result of modulus maxima algorithm；（d）Residuals between results of modulus maxima algorithm and original signal

表1 几种算法均方误差（MSE）及信噪比（SNR）Table 1 Mean squared error（MSE）and signal to noise ratio（SNR）of the algorithms

3.2 改进算法对合成地震信号的去噪处理

图5为用Ricker子波合成的含噪地震信号剖面图，信噪比为18dB.具体参数为：深度100m，反射层上层速度2 000m／s，下层速度3 000m／s，最小偏移距10m，道数40，密度为1，记录时间长度512ms.采用小波变换模极大值去噪方法与改进的去噪方法进行处理.图6为小波熵与相关性结合的模极大值去噪后的剖面图；图7为采用小波变换模极大值去噪后的剖面图.两种去噪方法均选取sym8小波，分解尺度均为4，阈值函数均采用软阈值函数，处理结果如图5—7所示.

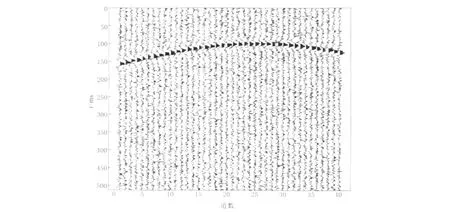
图5 合成的含噪地震信号剖面图Fig.5 Synthetic seismic section with noise

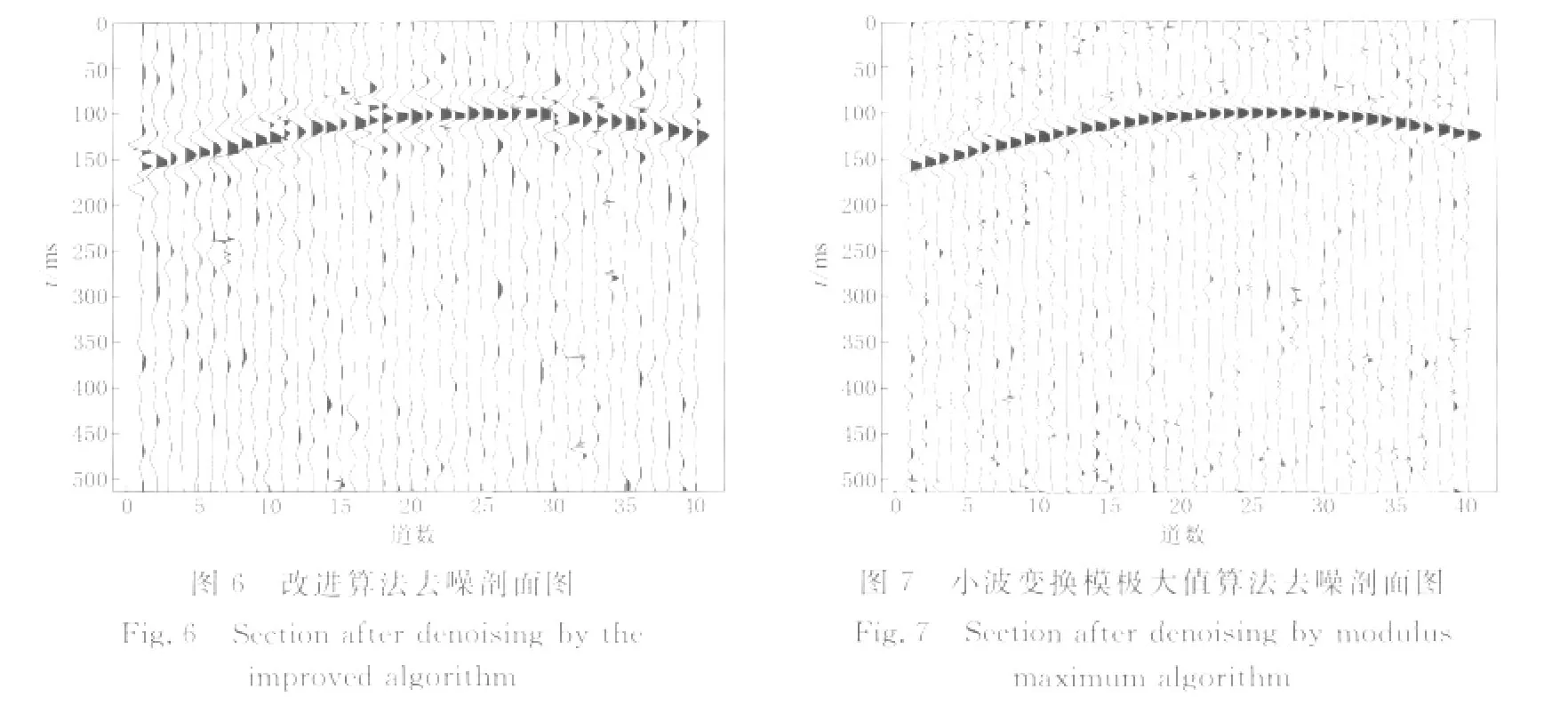
从图6和图7中可以看出，两种去噪方法都基本上抑制了噪声，但小波变换模极大值去噪后含有的噪声比改进算法去噪后含有的噪声多，并且小波变换模极大值去噪削弱了同相轴，有效信号有所损失.改进算法去噪后的信噪比为25.364 2dB，小波变换模极大值算法去噪后的信噪比为24.432 6dB，证明了改进算法的有效性，并体现了其优越性.

3.3 改进算法在实际地震信号去噪中的应用

从某实际地震信号中取出50道数据进行处理.图8为50道实际地震信号剖面图，采样点为1 024，采样间隔2ms；图9为改进算法去噪后的剖面图；图10为小波变换模极大值方法去噪后的剖面图.两种算法在去噪过程中均采用sym8小波，分解尺度均为4，阈值函数均采用软阈值函数，处理结果如图8—10所示.

从图8中可以看出，实际地震信号中含有很大的噪声，使剖面质量变差.从图9和图10中可以看出，两种去噪算法都很好地抑制了噪声，使同相轴变得比较清晰.但小波变换模极大值去噪算法在有些地方削弱了同相轴，如在第40道与第50道之间、采样点在200左右的地方，同相轴被削弱，有效信号有所损失；而改进算法基本没有削弱同相轴，有效信号也得到了很好的保留，这就证明了改进算法的有效性.

图10 小波变换模极大值去噪算法去噪后的地震信号剖面Fig.10 Practical seismic profile after denoising by modulus maxima algorithm

4 讨论与结论

小波变换模极大值去噪算法是一种有很好的理论保证但稳定性欠佳的去噪算法，表现在搜索模极大值传播点时容易出现错选和漏选现象，而且在确定最大尺度上的阈值时一般由经验选取.将本文提出的小波熵与相关性相结合的小波模极大值去噪算法应用于含噪的Ricker子波、合成地震信号和实际地震信号的去噪处理中，可以看出，改进的模极大值去噪算法的信噪比比小波变换模极大值去噪算法的信噪比高，均方误差小，对合成地震信号和实际地震信号进行去噪处理时，同相轴基本不被削弱，有效信号得到了很好的保留.改进算法在选取最大尺度的阈值时是根据小波熵来选取的，比根据经验选取更可靠；在确定各个尺度上的模极大值点时，将各尺度上根据逐级搜索得到的模极大值点与各尺度的相关性处理保留下来的高频信号的位置进行比较，避免了错选现象.改进的模极大值去噪算法可根据信号自身的能量特征自适应地确定最大尺度上的阈值，利用相关性解决了搜索过程中出现的模极大值错选问题，具有较好的去噪效果.

陈德智，唐磊，盛剑霓，王恒利.1998.由小波变换的模极大值快速重构信号［J］.电子学报，26（9）：82－85.

段炜.2008.基于小波变换的探地雷达信号去噪方法研究［D］.长沙：中南大学：43－54.

姜弢，刘庆普，胡留军.2002.地震信号去噪的小波方法研究［J］.哈尔滨工程大学学报，23（4）：86－89.

蒋鹏.2004.小波理论在信号去噪和数据压缩的应用研究［D］.杭州：浙江大学：47－59.

孔祥茜，吴继伟，岳继光.2005.地震信号小波变换的去噪方法［J］.计算机辅助工程，14（3）：52－56.

李华.2000.小波理论分析及其在地震信号处理中的应用研究［D］.成都：成都理工学院：43－52.

陆基孟.2005.地震勘探原理下册［M］.北京：石油大学出版社：312－328.

潘洪屏.2011.基于小波分析技术的地震信号去噪方法研究［D］.大庆：东北石油大学：38－40.

孙丰荣，翟广涛，李艳玲，刘泽，张梅，张运.2005.由小波变换模极大值重构信号的快速算法［J］.小型微型计算机系统，26（12）：2147－2149.

孙延奎.2005.小波分析及其应用［M］.北京：机械工业出版社：224－236.

田金文，高谦，杜拥军.2001.基于小波变换模极大值的地震信号去噪处理方法［J］.江汉石油学院学报，23（1）：22－25.

王秀明.2007.应用地球物理方法原理［M］.北京：石油工业出版社：23－25.

徐长发，李国宽.2004.实用小波方法［M］.武汉：华中科技大学出版社：107－119.

姚胜利.2007.地震信号的小波去噪方法研究［D］.长沙：中南大学：22－37.

张荣标，胡海燕，冯友兵.2007.基于小波熵的微弱信号检测方法研究［J］.仪器仪表学报，28（11）：2078－2083.

张媛玲.2001.小波分析在地震勘探资料处理中的应用［D］.沈阳：沈阳工业大学：12－14，34－43.

周怀来.2006.基于小波变换的地震信号去噪方法研究与应用［D］.成都：成都理工大学：1－7.

朱晓明.2007.工程地震信号去噪技术研究［D］.青岛：中国海洋大学：1－14.

Alnashash H A，Paul J S.2003.Wavelet entropy method for EEG analysis application to global brain injury［C］∥IEEE EMBSConferenceonNeuralEngineering.Capri Island，Italy.3：348－351.

Donoho D.1995.De－noising by soft－thresholding［J］.IEEETransonIT，3：613－627.

He Z Y，Cai Y M.2004.A study of wavelet entropy theory and its application in power system［C］∥IEEEInternational ConferenceonIntelligentMechatronicsandAutomation.Chengdu，China.8：847－851.

Hsung T C，Lun D P K.1999.Denoising by singularity detection［J］.IEEETransactionsonSignalProcessing，47（11）：3139－3144.

Mallat S G，Zhong S.1992.Characterization of signals from multiscale edges［J］.IEEETransactionsonPattern AnalysisandMachineIntelligence，14（7）：710－732.

Witkin A P.1983.Scale space filtering［C］∥ProceedingsoftheEighthInternationalJointConferenceonArtificial Intelligence.Karlsruhe，Germany：1019－1022.

Ykhlef F，Arezki M.2004.A wavelet denoising method to improve detection with ultrasonic signal［C］∥IEEEInternationalConferenceonIndustrialTechnology.Hammamet，Tunisia：1422－1425.

李 文 东北石油大学副教授，硕士研究生导师.1993年大庆石油学院机械系工业与民用建筑专业毕业，获学士学位；2001年哈尔滨工业大学结构工程专业毕业，获硕士学位.主要从事抗震减灾研究、地震信息处理及项目管理工作.

Wavelet modulus maxima denoising of seismic signals based on combined wavelet entropy and correlation

Li Wen Liu Xia Duan Yubo Yao Jianhong Liu Jicheng Pan Hongping

（NortheastPetroleumUniversity，Daqing163318，China）

In wavelet modulus maxima denoising algorithms，high－frequency wavelet coefficients are all considered as noises，and the useful information in them is ignored，therefore，modulus maxima pickup points are wrongly selected and the calculated noise variances still contain useful information.To solve these problems，this paper proposed a wavelet modulus maxima denoising algorithm which combines wavelet entropy with correlation.The effective signal location is determined by correlation processing of high－frequency wavelet coefficients.The high－frequency wavelet coefficients on the maximum scale are divided into several small zones，and the interval wavelet entropy is calculated.With the mean value of high－frequency wavelet coefficients in the wavelet entropy maxima interval as noise variance，the threshold value of the maxima scale is calculated according to the formula presented by Donoho in 1995.By comparing locations of the maxima point obtained by comparison the threshold values with locations of the useful information obtained by correlation processing，the modulus maxima of the same position are retained and modulus maxima points of different positions caused by noises are eliminated.The modulus maxima of each level are searched with the Adhoc algorithm step by step and the denoised signals are reconstructed by alternating projection algorithm.This improved algorithm realized adaptive selection of threshold values and removal of wrongly selected modulus maxima pickup points.Our method and a conventional denoising method were both applied to simulation signal processing，and comparative analysis verified effectiveness of our improved method.

modulus maxima；wavelet entropy；correlation；seismic signal；denoising

10.3969／j.issn.0253－3782.2012.06.010

P315

A

李文，刘霞，段玉波，姚建红，刘继承，潘洪屏.2012.基于小波熵与相关性相结合的小波模极大值地震信号去噪.地震学报，34（6）：841－850.

Li Wen，Liu Xia，Duan Yubo，Yao Jianhong，Liu Jicheng，Pan Hongping.2012.Wavelet modulus maxima denoising of seismic signals based on combined wavelet entropy and correlation.ActaSeismologicaSinica，34（6）：841－850.

教育部重点项目（210056）、教育部新世纪人才计划（NCET－09－0127）和黑龙江省新世纪人才计划（1154NCET001）资助.

2011－12－12收到初稿，2012－07－04决定采用修改稿.

e－mail：liuxia2k＠163.com