核实数据下的递归核密度估计

宇世航, 赵世舜

(1. 齐齐哈尔大学 理学院, 黑龙江 齐齐哈尔 161006; 2. 吉林大学 数学学院, 长春 130012)

基于替代数据和核实样本推断的研究目前已有许多结果[1-10]. Sepanski等[1]研究了基于核实数据的非线性EV模型; Wolvreton等[11]提出了f(x)的递归型核密度估计:

由于递归型核密度估计在添加样本点时, 不必重新计算所有项, 只需计算添加项, 因此使计算更方便. 基于此, 本文考虑借助于核实数据, 构造一递归型概率密度估计量, 并研究其渐近正态性.

1 主要结果

于是在一些正则条件下,f(x)可被如下递归核估计量一致估计:

定义

AppendixA条件:

(A·f):f(x)是k阶有界可导的;

(A·K):K(·)在有界支撑集上是k阶非负有界的核函数;

定理1在AppendixA条件下, 有

证明:

(3)

这里C为任意常数, 且在不同处可取不同的值. 于是, 由式(3)～(6)有

则

从而

其中

而

及条件(A·bn,ηn), 可得

(8)

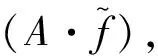
同理, 有

(10)

于是由式(2)～(10), 有

(11)

同理, 由(A·f),(A·K),(A·hj), 得

(13)

综上所述, 有

令

由条件(A·K)和(A·h), 有

由式(15)～(17), 显然有

I1→N(0,θ1σ2(x)),

(18)

I2→N(0,θ2σ2(x)),

(19)

而

故结合式(15),(18)～(20)可得

2 模拟结果

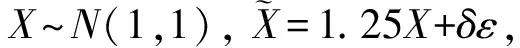
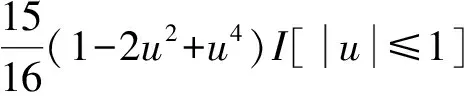
(n,N)=(20,100),(50,100),(50,300),(100,300),

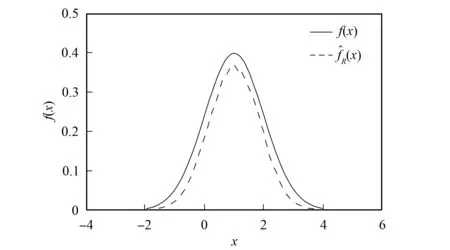
图1 n=20, N=100时的模拟结果Fig.1 Simulation result for n=20, N=100

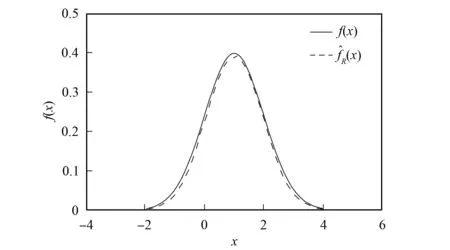
图2 n=50, N=100时的模拟结果Fig.2 Simulation result for n=50, N=100

图3 n=50, N=300时的模拟结果Fig.3 Simulation result for n=50, N=300

图4 n=100, N=300时的模拟结果Fig.4 Simulation result for n=100, N=300

由图1～图4可见, 给定样本总数N的情况下, 模拟效果随核实数据样本容量n的增加而渐好； 当固定核实数据样本容量n时, 顶部随样本总量N的增加模拟效果渐好, 尾部变差； 如果同时增大N和n, 模拟结果更趋近于f(x), 并且也更平滑.

[1] Sepanski J H, Lee L F. Semiparametric Estimation of Nonlinear Error-in-Variables Models with Validation Study [J]. J Nonparametric Statist, 1995, 4: 365-394.

[2] WANG Qi-hua. Estimation of Partial Linear Error-in-Variables Model with Validation Data [J]. J Multivaiate Anal, 1999, 69: 30-64.

[3] WANG Qi-hua. Estimation of Linear Error-in-Covariables Models with Validation Data under Random Censorship [J]. J Multivariate Anal, 2000, 74(2): 245-266.

[4] WANG Qi-hua, Rao J N K. Empirical Likelihood-Based Inference in Linear Error-in-Corariables Models with Validation Data [J]. Bioraetrika, 2002, 89(2): 345-358.

[6] WANG Qi-hua, YU Ke-ming. Likelihood-Based Kernel Estimation in Semiparametric Errors-in-Covariables Models with Validation Data [J]. Journal of Multivariate Analysis, 2007, 98(3): 455-480.

[7] XUE Liu-gen. Empirical Likelihood Inference in Nonlinear Semiparanetric EV Models with Validation Data [J]. Acta Mathematica Sinica: Chinese Series, 2006, 49(1): 145-154. (薛留根. 核实数据下非线性半参数EV模型的经验似然推断 [J]. 数学学报: 中文版, 2006, 49(1): 145-154.)

[8] DAI Peng-jie, SUN Zhi-hua, WANG Peng. Model Checking for General Linear Error-in-Covariables Model with Validation Data [J]. Acta Mathematica Sinica, 2010, 23(6): 1153-1166.

[9] WANG Qi-hua. Dimension Reduction in Partly Linear Error-in-Response Models with Validation Data [J]. Journal of Multivariate Analysis, 2003, 85(2): 234-252.

[10] DU Li-lun, ZOU Chang-liang, WANG Zhao-jun. Nonparmetric Regression Function Estimation for Errors-in-Variables Models with Validation Data [J]. Statistica Sinica, 2011, 21: 1093-1113.

[11] Wolvreton C T, Wagner T J. Asymptotically Optimal Discriminant Functions for Pattern Classification [J]. IEEE Trans, 1969, 15(2): 258-265.

[12] Rao B L S P. Nonparametric Functional Estimation [M]. London: Academic Press, 1983.