气幕防波堤消波性能影响因素数值模拟研究

张成兴，李丽慧，马 加

(1.许昌学院城市与环境学院，河南许昌 461000;2.大连海洋大学海洋科技与环境学院，辽宁大连 116023)

1 研究背景

气幕防波堤结构主要是由表面上开有大量小孔的管子和空气压缩机组成。在需要掩护的海域外侧水底铺设一条表面上开有大量小孔的管子，如水深很大则可安置在水下一定深度处。压缩空气由气压站沿导管或干管(如果孔管有分支)输移至孔管部分。压气站是安置在岸上或者安置在离岸很远的某处，例如在普通突堤的堤头上，也可以将压气站安置在船上［1］。气幕防波堤结构的优点在于:当喷气管安设得足够深时，船舶可以在任何地方进港，畅行无阻。当水深很大，波浪周期较小，而且是短时间的偶然工作时，利用这种消波方式是经济合理的。如用于具有足够电能来源的大型水库中，掩护开阔海岸中的码头地带，在强烈风暴时封闭入港的口门，当船队过闸时掩护入闸航道、掩护一部分水域以进行施工及打捞沉船等［2］。此外，气幕防波堤作为一种特殊形式的防波堤，与固定式防波堤相比，具有移动性、临时机动性、可重复使用、不受水深和地质条件限制、不影响水流、泥沙的运动条件，可以很容易通过抛锚固定或通过锚链固定在抛入水中的预制重物上等优点［3］。

气幕防波堤最早于1907年由美国人Brasher提出用来保护海岸工程，1915年在El Segundo，California建成了第二座气幕防波堤。但由于其消波效果不理想，很多学者对它的进一步研究失去了兴趣。1924年 Admiraly、1935年俄国科学家、1936年Thysse教授等都开展了试验研究。二战期间的诺曼底战争促发了White和Taylor对气幕和水幕防波堤的研究和分析。20世纪50年代Laurie在多佛为了保护铁路轮渡码头设计了气幕防波堤结构。Carr和Schiff于美国加州理工学院利用模型水槽对气幕防波堤进行了研究，他们的研究成果成为多佛气幕防波堤的设计基础［4］。Evans［5］于 1954 年开展了一系列的模型研究，以此来衔接 Taylor［6］的理论工作。Bulson总结了自己及前人的理论研究和试验工作。认为气幕防波堤的消波机理是由于气幕的存在而产生的表面水平流，并根据大量试验结果给出了气幕防波堤设计的相关经验公式，可用来参考设计气幕防波堤所产生的表面水平流的流速、厚度以及一定的消波条件下所需的供气量［7］。

国内外学者虽然在气幕防波堤的消波机理和设计方法等方面开展了较长时间的研究工作，但由于气幕防波堤在工作时发生的空气和水的动力现象十分复杂，当前有关气幕防波堤的研究进展十分有限，有关可供实际应用的技术资料仍很少。本文研究工作的重点在于通过数值模拟，在不同长度比尺条件下，不同入射波浪周期和入射波高，以及不同的管道淹没深度条件下对气幕防波堤消波性能进行分析比较，进一步明确影响气幕防波堤消波性能的主要因素，为气幕防波堤的设计和实际应用提供参考依据。

2 数学模型

本文将空气和水组成的两相流体看成是一种变密度单流体，以连续方程、雷诺平均方程和k-ε方程为控制方程，采用VOF(Volume of Fluid)方法追踪两相流界面。通过UDF(User Defined Function)在连续方程中添加质量源项Sm和动量方程中添加动量源项实现了气幕防波堤结构的数值模拟。通过模型验证，在确保数学模型准确的前提下，对可能影响到气幕防波堤消波性能的其他因素进行了大量的数值模拟计算，确定了这些因素对气幕防波堤结构消波性能的影响。

2.1 控制方程

因本文所研究的流体只有空气和水两相流体构成，因此将空气与水组成的混合物看成是一种变密度单流体，其密度ρ和黏性系数μ可采用式(1)和式(2)计算。

式(1)和式(2)中的a0为空气的体积分数，a1为水的体积分数;相应地ρ0和μ0分别为空气的密度和黏性系数;ρ1和μ1分别为水的密度和黏性系数。空气和水的体积分数可统一用aq表示，其中q=0，1。aq需要满足如下方程:

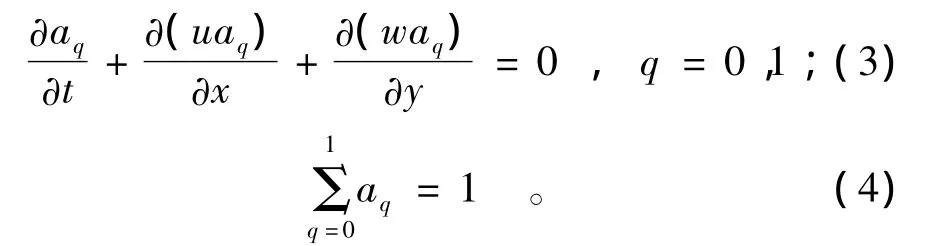
变密度单流体的控制方程表达式为式(5)至(7)。式(5)至(7)与单相流的连续方程和雷诺平均N-S方程的形式相同［8］，只是方程中的密度ρ和黏性系数μ由式(1)与式(2)确定，速度和压力定义为变密度单流体的速度和压力平均值。

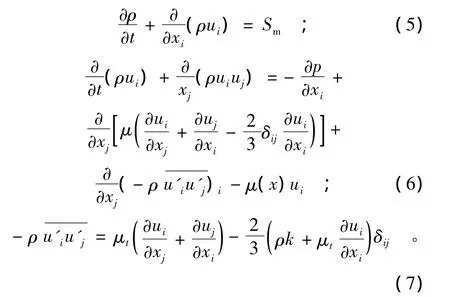
式(7)中的 μt为湍流黏性系数，μt= ρCμk2/ε。其中Cμ为系数，取Cμ=0.09;湍流动能k和湍流动能耗散率ε采用式(8)与式(9)的标准 k-ε方程［9］。由于将空气和水两相流体处理为一种变密度单流体，因此标准k-ε方程的系数也同样适用。

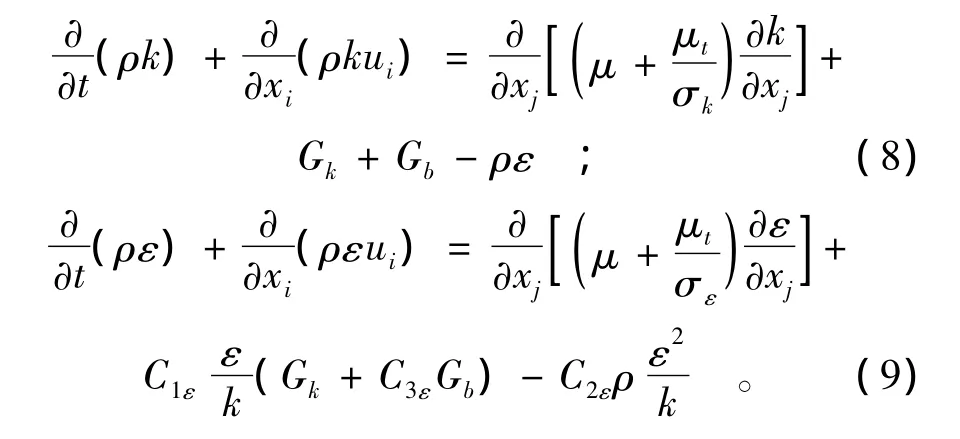
式(8)与式(9)中的Gk表示由层流速度梯度而产生的湍流动能;Gb是由浮力产生的湍流动能;C1ε，C2ε是 常 量，取 C1ε=1.44，C2ε=1.92;C3ε=是k方程和ε方程的湍流 Prandtl数，取 σk=1.0，σε=1.3。

2.2 边界条件及算法

气幕防波堤数值模型示意图如图1，图中左边界AB为造波动边界，右边界CD取无滑移直墙边界条件，墙前的尾端消波采用阻尼层消波。上边界AD取压力入口边界条件，底边界BC取无滑移直墙边界条件［10－11］。

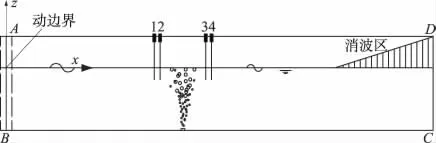
图1 气幕防波堤数值模型示意图Fig.1 Sketch of the air bubbles breakwater model

气幕防波堤数值模型左边的造波动边界选用推板式造波，数值波浪水槽尾端采用阻尼层消波，即利用数值阻尼的方法在阻尼层中使波浪的速度和压力逐渐减小来达到消波的目的［12］。可通过在数值波浪水槽尾端添加附加动量源项μ(x)ui于动量方程式(6)右端来实现，其中

式中:xl为阻尼层末端位置;x0为阻尼层起始位置。气幕的产生通过设置连续方程式(5)右端的质量源项Sm来实现。

基于网格划分软件Gambit对图1所示的气幕防波堤模型进行流动区域几何形状的构建、边界类型的确定以及网格的生成。动量方程的离散格式以及k-ε方程离散格式均使用一阶迎风格式。对离散后得到的线性方程组的求解采用分离式解法，采用VOF方法追踪气液两相的界面。对压力插值方式选用体积力加权方式。对压力速度耦合方式，选用隐式分裂算法。

2.3 模型验证

为验证气幕防波堤数值建模的合理性，对图1所示的气幕防波堤数值计算模型进行数值模拟计算。长度比尺选取1∶10，波浪参数和供气量参数的选取与试验研究相同［1］，即选取波高 H=0.355 m，水深 d=1.2 m，周期 T=1.58 s，1.91 s，供气量Qm=5，10，15，20 m3/(h·m)。

图2中的图(a)和图(b)分别给出了不同供气量Qm条件下入射波浪周期 T分别为1.58 s和1.91 s时透射系数Ctm的试验结果和数值结果对比图。可以看出，无论入射波浪周期T大小，气幕防波堤透射系数Ctm均随着供气量的增加而降低，说明供气量Qm是影响气幕防波堤消波性能的一个影响因素。此外，从图2还可以看出，透射系数Ctm的试验结果和数值结果相差很小，相对误差最大为4.8%，表明本文气幕防波堤数学模型建模的合理性。

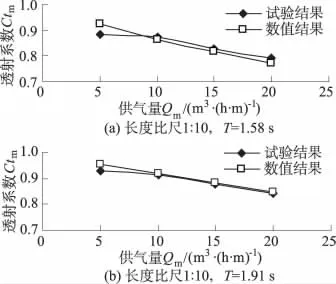
图2 不同供气量Qm条件下试验和数值模拟透射系数Ctm对比图Fig.2 Comparison of the transmission coefficients Ctmwith different air amounts Qmby test and numerical simulation

3 计算结果和分析

在气幕防波堤数学模型得到验证的前提下，对不同入射波浪波高Hi、不同管道埋深D等情况下的气幕防波堤消波性能进行了数值模拟研究，并根据得到的数值模拟结果进行了分析和比较，确定了入射波浪波高Hi、管道埋深D对气幕防波堤消波性能的影响。

3.1 入射波浪波高Hi的影响

为了探讨入射波高Hi对气幕防波堤的消波性能影响，本文以原型波浪周期T=4，5，6 s，水深d=12 m，波高 H=2.55，3.05，3.55 m为算例，同时考虑了空气可压缩性对气幕防波堤消波性能的影响，数值模拟了不同供气量Qp情况下，不同入射波浪波高Hi对气幕防波堤消波性能的影响。

图3中的图(a)和图(b)分别为不同供气量Qp情况下，入射波浪周期T=4，5 s情况下不同入射波浪波高Hi对气幕防波堤结构消波效果的影响图。

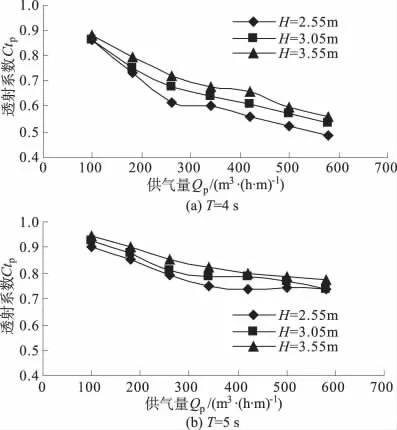
图3 不同入射波高Hi对透射系数Ctp的影响Fig.3 The influence of incident wave height Hion transmission coefficient Ctp

由图3可以看出，无论入射波浪周期T如何，在保持水深d一定的情况下，气幕防波堤对入射波浪波高Hi较大的波浪消波效果劣于入射波浪波高Hi较小的波浪消波效果。同时从图3还可以得到这样的结论:在入射波浪周期T一定，水深d一定情况下，无论入射波高Hi大小，气幕防波堤的消波性能都随着供气量的增加而增强，这和前面数值模拟结果得到的结论也是一致的。

出现上面这样的结论可以利用波能来说明。由于水深d一定，入射波浪周期T一定情况下，入射波浪波高Hi大的波浪具有的波能也大。在供气量Qp一定情况下，所产生的消波能量也是一定的，所以在相同供气量Qp作用下，对于入射波高Hi较大波浪情况，气幕防波堤的消波性能要差于入射波高Hi较小波浪情况。

3.2 供气管道淹没深度D的影响

当供气量Qp一定的情况下，考虑管道淹没深度D对气幕防波堤消波效果的影响。其中，管道埋深D定义为管道在水中的位置到水面的垂直距离。本文共设计了3种淹没深度，分别为6，8，12 m。每种淹没深度采用的供气量Qp共7种情况，3种不同的入射波浪周期T。

图4中的图(a)和图(b)为入射波浪周期T分别为4 s和6 s情况下，不同管道埋深D、不同供气量Qp情况下气幕防波堤的消波效果图。

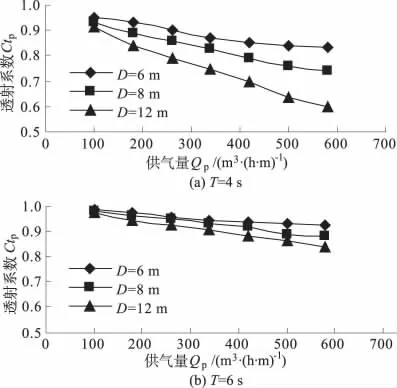
图4 不同管道埋深D对透射系数Ctp的影响Fig.4 The influence of submerged pipe depth D on transmission coefficient Ctp

从图4中可以得到这样的结论:无论入射波浪周期T如何，在同一供气量Qp的作用下，其透射系数Ctp均随着管道埋深D的增加而减小，说明管道埋深D越大，气幕防波堤的消波效果越好;此外，同一供气量Qp的作用下，入射波浪周期T较短情况，管道埋深D的大小对入射波浪的消波效果有着明显的干预作用。而对于入射波浪周期T较长的情况，管道埋深D的改变对入射波浪的消波效果没有短周期入射波浪的消波效果明显。同时从图4还可以看出，供气量Qp在气幕防波堤消波性能方面起着着决定性的作用，同样和前面得到的结论也是一致的。

4 结论

本文基于试验条件和试验数据，以连续方程，雷诺时均方程和k-ε方程为控制方程，在连续方程和动量方程分别添加质量源项和动量源项实现了气幕防波堤的数学模拟。通过和试验数据进行比较，表明本文气幕防波堤数学模型建立的合理性，进而对其他影响气幕防波堤消波性能因素进行数值模拟和分析。通过本文的试验研究和数值模拟研究得到结论如下:

(1)气幕防波堤消波机理是由于气幕的存在，在水体中产生2个方向相反的环流，进而在液面一定深度处形成水平流。

(2)气幕防波堤消波性能和供气量相关，在其他条件不变的情况下，增大供气量可以增强气幕防波堤的消波效果。

(3)入射波浪周期T也是影响气幕防波堤消波性能的主要因素，入射波浪周期T越短，气幕防波堤的消波效果越明显，反之则不明显，说明气幕防波堤对短周期入射波浪消波效果好。

(4)在入射波浪周期一定，供气量一定，气幕防波堤对入射波浪波高Hi较小的情况消波效果要好于入射波高Hi较大的情况。

(5)水深一定，供气量一定，供气管道埋深D不同，气幕防波堤对相同入射波浪的消波效果不同。管道埋深D越大，消波效果越好。

［1］王国玉.特种防波堤结构形式及水动力学特性研究［D］.大连:大连理工大学，2005.(WANG Guo-yu.Investigation on the Structure Type and Performance of Special Breakwaters［D］.Dalian:Dalian University of Technology，2005.(in Chinese))

［2］王国玉，王永学，李广伟.气幕防波堤消波性能试验研究［J］.中国造船，2004，45(增):103－109.(WANG Guo-yu，WANG Yong-xue，LI Guang-wei.Experimental Study on the Performance of Air Bubbles Breakwater［J］.Shipbuilding of China，2004，45(Sup.):103 － 109.(in Chinese))

［3］童朝峰，严以新.浮式防波堤消浪特征研究［J］.水运工程，2002，(8):32 － 35.(TONG Chao-feng，YAN Yixin.Study on the Decaying Wave Feature of Floating Breakwater［J］.Port ＆ Waterway Engineering，2002，(8):32 －35.(in Chinese))

［4］BULSON P S.Transportable Breakwaters［J］.The Dock and Harbour Authority，1967，XLVIII(560):41 －46.

［5］EVANS J T.Pneumatical and Similar Breakwaters［J］.Proceedings of the Royal Society A:Mathematical，Physical and Engineering Sciences，1955，231(1187):457 －465.

［6］GEOFFREY T.The Action of a Surface Current Used as a Breakwater［J］.Proceedings of the Royal Society A:Mathematical，Physical and Engineering Sciences，1955，231(1187):466－478.

［7］BULSON P S.Bubble Breakwaters with Intermittent Air Supply［J］.The Dock and Harbour Aurhority，1963，XLIV(514):129－134.

［8］韩占忠，王 敬，兰小平.FLUENT流体工程仿真计算实例与应用［M］.北京:北京理工大学出版社，2004.(HAN Zhan-zhong，WANG Jing，LAN Xiao-ping.Examples and Applications of FLUENT Fluids Engineering Simulation［M］.Beijing:Beijing Institute of Technology Press，2004.(in Chinese))

［9］王瑞金，张 凯，王 刚.FLUENT技术基础与应用实例［M］.北京:清华大学出版社，2007.(WANG Ruijin，ZHANG Kai，WANG Gang.Technical Foundations and Application Examples of FLUENT［M］.Beijing:Tsinghua University Press，2007.(in Chinese))

［10］李 凌.黏性流中水波与浮式结构物相互作用的数值模拟研究［D］.上海:上海交通大学，2007.(LI Ling.Numerical Simulation of Interaction of Water Waves and Floating Structures in a Viscous Fluid［D］.Shanghai:Shanghai Jiao Tong University，2007.(in Chinese))

［11］李胜忠.基于Fluent的二维数值波浪水槽研究［D］.哈尔滨:哈尔滨工业大学，2006.(LI Sheng-zhong.Study on 2-D Numerical Wave Tank Based on Software FLUENT［D］.Harbin:Harbin Institute of Technology，2006.(in Chinese))

［12］李 凌，林兆伟，尤云祥，等.基于动量源方法的黏性流数值波浪水槽［J］.水动力学研究与进展(A辑)，2007，22(1):76 － 82.(LI Ling，LIN Zhao-wei，YOU Yun-xiang，et al.The Numerical Wave Flume of the Viscous Fluid Based on the Momentum Source Method［J］.Journal of Hydrodynamics(Ser.A)，2007，22(1):76 －82.(in Chinese))