高速离心泵隔舌对流体激振力的影响研究✳

窦 唯,刘占生

(1.北京航天动力研究所,北京 100076;2.哈尔滨工业大学能源科学与工程学院,黑龙江哈尔滨 150001)

引 言

高速离心泵在国民经济各领域起到了极其重要的作用,其动态性能的优劣关系到离心泵的运行稳定性。在高速离心泵振动引发的故障中,因压力脉动引起的流体激振占离心泵损坏的大部分。离心泵在传输流体介质过程中,受到泵内流体对叶轮的激励作用,这些力作为泵转子的外部激励,影响着泵转子的动力响应与稳定性。国内外许多学者对泵内流体诱发的压力脉动进行了研究。Jorge L等测量了普通蜗壳内的压力脉动[1～3],发现隔舌与叶轮的相互作用在蜗壳压力脉动和产生噪音方面起着主导作用;Kitano Majidi等对离心泵内流场进行了数值模拟[4～8],指出叶轮和蜗壳内流动的非稳定特性呈现周期性,在叶轮出口和蜗壳内的压力脉动较强。朱荣生分析了双叶片泵内压力脉动特点及其主要影响因素[9],指出双叶片泵内压力波动呈正弦周期性变化,进口处监测点压力波周期为其他监测点的 2倍;王洋等对离心泵内部不稳定流场压力脉动特性进行了分析[10,11],指出在不同工况下,叶片通过频率均占主导地位,压力面脉动幅值大于吸力面脉动幅值,蜗壳出口同一测面脉动情况近似;刘占生对离心泵变工况流场及叶轮流体激振力进行了研究[12],指出离心泵偏离设计工况时稳态作用力会显著增加。

本文采用 Reyno ld时均方法,对高速离心泵全部过流部件流场进行了三维非定常数值模拟,分析了泵内的压力场分布,计算了不同转速下的径向力脉动并进行了频谱分析,重点研究了隔舌厚度变化对泵脉动激振力的影响。这些工作为泵的设计改型提供了参考依据。

1 高速离心泵内流计算方法

1.1 计算区域

计算区域包括离心泵进口段、叶轮、蜗壳和出口段,如图1所示。叶轮与蜗壳、叶轮与进口段间分别划分 2个滑移界面,针对计算域空间复杂的特点,全流域内采用适应性强的非结构化四面体网格划分。

图1 泵内部流场三维模型图Fig.1 3D model of pump inner flow field

1.2 控制方程及湍流模型

采用分离求解法,非定常计算时采用一阶隐式格式,取时间步长τ=10-4s。压力项采用二阶中心差分格式,其他项采用二阶迎风差分格式。使用速度入口及流动充分发展出口边界条件,近壁区采用速度分布对数律固壁函数。采用最大残差方法以监视变量达到 10-3来判断计算收敛。

1.3 方程离散与求解

采用分离求解法,非定常计算时采用一阶隐式格式,取时间步长f=10-4s。压力项采用二阶中心差分格式,其他项采用二阶迎风差分格式。使用速度入口及流动充分发展出口边界条件,近壁区采用速度分布对数律固壁函数。采用最大残差方法以监视变量达到 10-3来判断计算收敛。

1.4 动静干涉处理

为了模拟进口和叶轮、叶轮和蜗壳之间的相对运动,分别在相邻区域间建立交界面。 Fluent软件描述动静区域间相对运动的方法主要有多参考系、混合面、滑移网格和动网格等模型,其中多参考系及混合面模型都假定流动为定常。非定常流动计算中,在进口和叶轮、叶轮和蜗壳间形成网格滑移的交界面。滑移网格模型可使在交界面两侧的网格相互滑动,而不要求交界面两侧的网格结点相互重合。但要计算交界面两侧的通量,并使其相等。为了计算交界面的通量,首先在每一新的时间步确定出交界面两边交界区的重合面。通过网格重合面的通量,是由交界面两边交界区的重合面计算,而不是用整个交界面计算。

2 计算结果分析

2.1 压力分布分析

叶轮在旋转过程中,由于叶轮的叶片数并不是无限多的,有限的几个叶片数将叶轮分为有限个周期对称的部分,但在每个部分通过隔舌的过程中,泵与隔舌的位置并不一致。在叶轮旋转,每个对称单元通过隔舌的过程中,压力并不是完全一致的。图2为泵内部流场计算结果中提取的压力云图。在一个叶片通过隔舌的过程中,泵内部的压力分布相似,但并不是完全一致,特别是在蜗壳隔舌部位存在差别。

图2 叶片相对于隔舌在不同位置时的压力云图Fig.2 The pressure distribution when the blade at different position to the tongue of volute

不同的压力分布,就使得泵的叶轮在一个叶片通过隔舌的过程中,叶轮周向的压力是存在一定的差别的,这就使得泵叶轮所受到的径向力也是存在一定的脉动现象的。

图3 叶轮内流场的压力云图Fig.3 The p ressure distribution in the impeller flow field

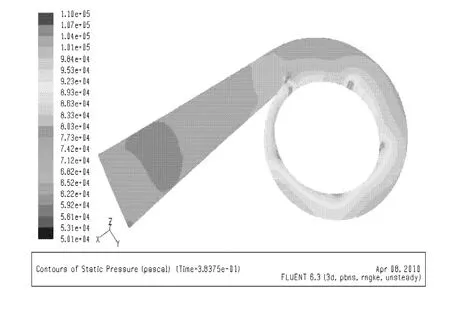
图4 蜗壳内流场的压力云图Fig.4 The pressure distribution in the volute flow field

图5 叶片两侧的压力云图Fig.5 The pressure distribution on two sides of blades

从泵内部流场的压力云图可以看出,泵内部的压力从进口管道逐渐增加,经过叶轮增速增压后,在蜗壳内压力进一步增加,最后在出口压力达到最大值。这与泵的工作原理相符,反映了计算结果的合理性。

本文主要分析泵叶轮主流内流动在叶轮上所引起的径向力脉动作用。通过对泵叶轮叶片上压力的积分,就可以得到泵叶轮所受到的主流激励力的大小。图5所示为泵叶片受压面和被压面上的压力分布。

本研究采用GIS技术和隶属函数模型对胶东半岛耕地地力进行评价，并对评价结果进行分析，并提出了耕地可持续利用建议与措施。主要结论如下：

在流场计算中,速度也是反映流动状况的重要参数。泵内部流场的速度云图如图6～8所示。从离心泵内部的速度云图可以看出,泵进口处速度较小,流体介质在进入叶轮后,速度随着叶轮半径的增加而增加很大,在蜗壳内则随着流动方向流速逐渐降低。泵内部的压力云图和速度云图都反映了泵工作过程中,流体介质的增压的过程。

图6 进口管道内的速度云图Fig.6 The velocity distribution in the in let flow field

图7 叶轮内流场的速度云图Fig.7 The velocity distribution in the impeller flow field

泵叶片的受压面上压力较大,而被压面上压力较小,特别是在叶片进口处,压力达到最小值,这里也是泵经常出现汽蚀的地方。在每一计算时刻下,对泵叶片上的压力进行积分,就可以得到泵在工作过程中,叶轮所受到的径向力大小及其变换规律。

图8 蜗壳内流场的速度云图Fig.8 The velocity distribution of the volute inner flow field

2.2 压力脉动频谱分析

分别计算了在6 000,9 000和15 000 r/m in下叶轮受力。各个转速下提取的脉动量及其傅里叶变化结果如下所示。图9～11为叶轮转速为 6 000 r/min时,泵叶轮受到的无量纲化的径向力、扭转力矩及其傅里叶变换结果。

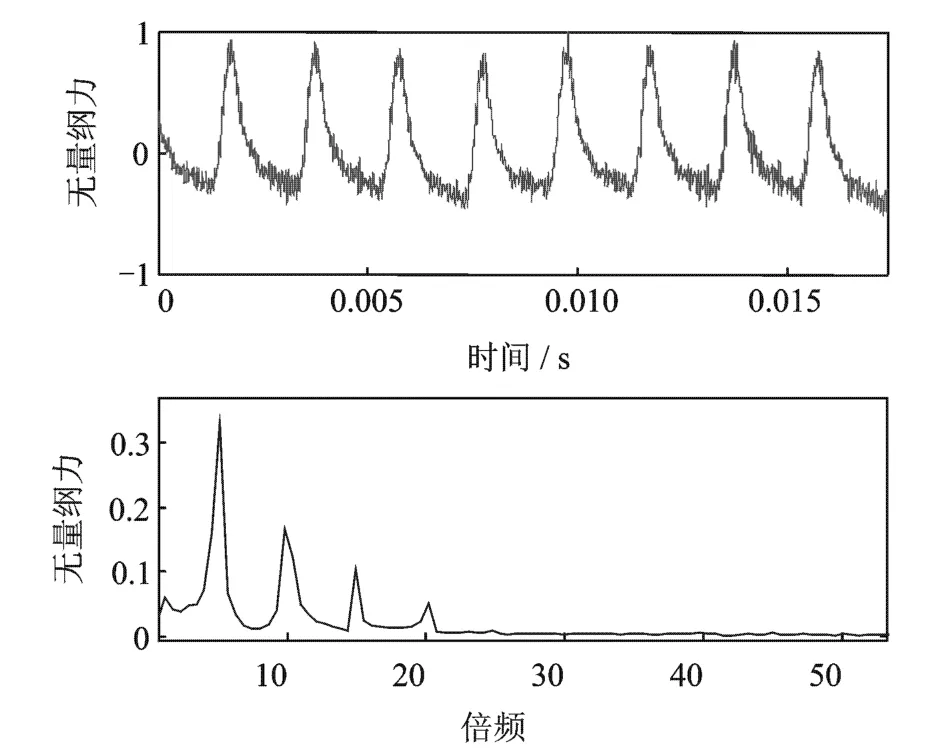
图9 无量纲化的X向力及其频谱图Fig.9 Dim ensionless force in X direc tion and its frequency spectrogram

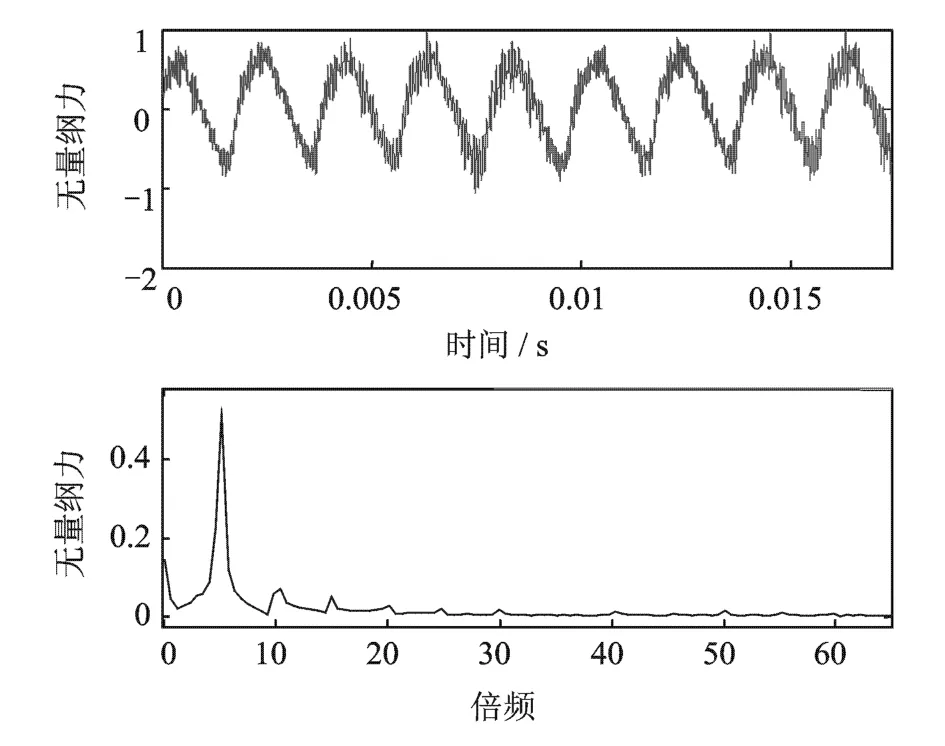
图10 无量纲化的Y向力及其频谱图Fig.10 Dimension less forces in Y direction and its frequency spectrogram

图11 无量纲化的 M Z向力及其频谱图Fig.11 Dimensionless mom ent in Z direction and its frequency spectrogram

从图9～10中可以看出,叶轮的受力可以分解为一个恒定力与一个脉动量的叠加。由于在转子动力学中,恒定力将会被泵转子的支撑轴承承受,在不考虑转子变形的情况下,对转子的振动的影响几乎可以不考虑。下面,就分别提取叶轮受力的脉动量,分析脉动量的特征,为进行泵转子的动力学分析提供力的特征。

图12和图13为叶轮转速为 9000 r/min时,泵叶轮受到的无量纲化的径向力及其傅里叶变换结果。

图14为叶轮转速为9000 r/min时,泵叶轮受到的无量纲化的扭转力矩及其傅里叶变换结果。

图15和图16为叶轮转速为15000 r/min时,泵叶轮受到的无量纲化的径向力及其傅里叶变换结果。

图17为叶轮转速为 15000 r/min时,泵叶轮受到的无量纲化的扭转力矩及其傅里叶变换结果。

从上面各个转速下叶轮所受的激振力的频率特征来看,叶轮受到的激振力的频率主要为叶片通过隔舌的频率,及转速的5倍频。同时,也存在叶片通过隔舌的高倍谐波频率成分,谐波的幅值随着倍数的增加而迅速减小。

图12 无量纲化的X向力及其频谱图Fig.12 Dimension less force in X direction and its frequency spec trogram

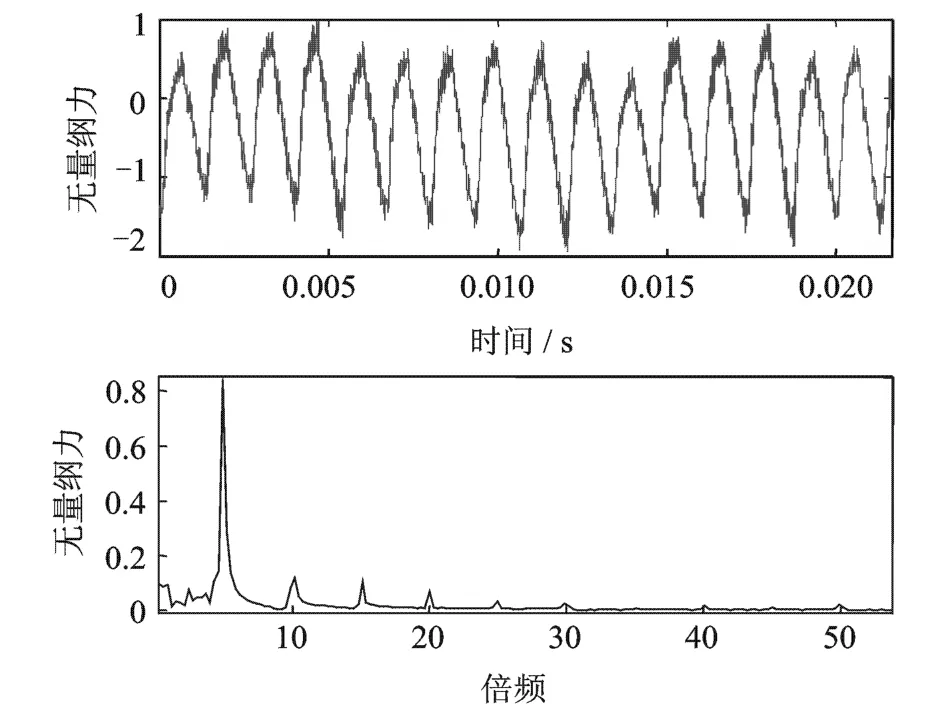
图13 无量纲化的Y向力及其频谱图Fig.13 Dimensionless force in Y direc tion and its frequency spectrogram

图14 无量纲化的M Z向力及其频谱图Fig.14 Dimension less moment in Z direction and its frequency spec trogram

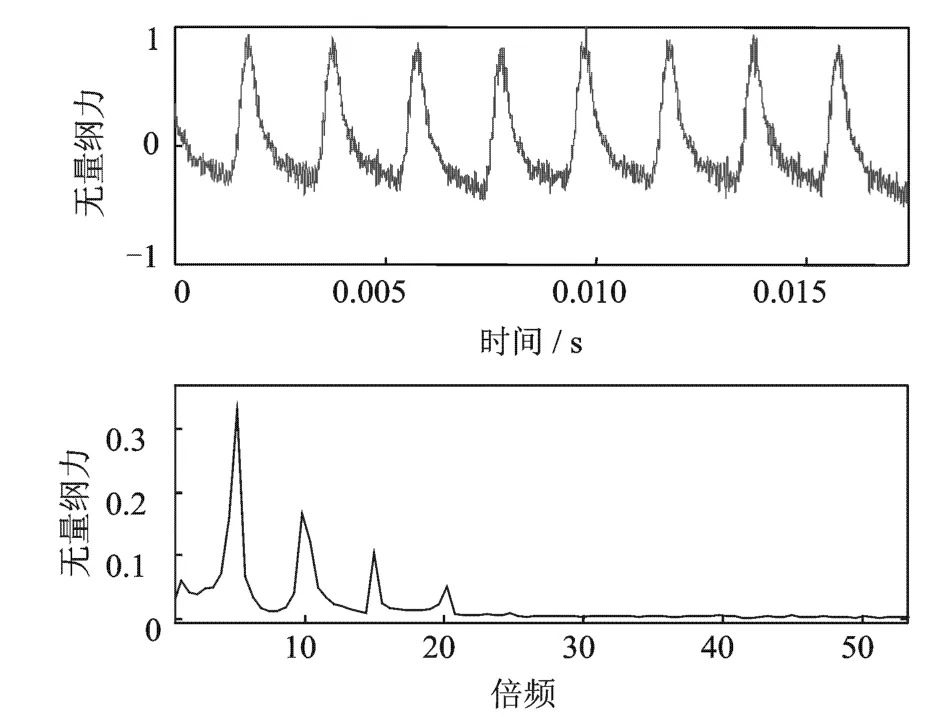
图15 无量纲化的X向力及其频谱图Fig.15 Dimensionless force in X direc tion and its frequency spectrogram

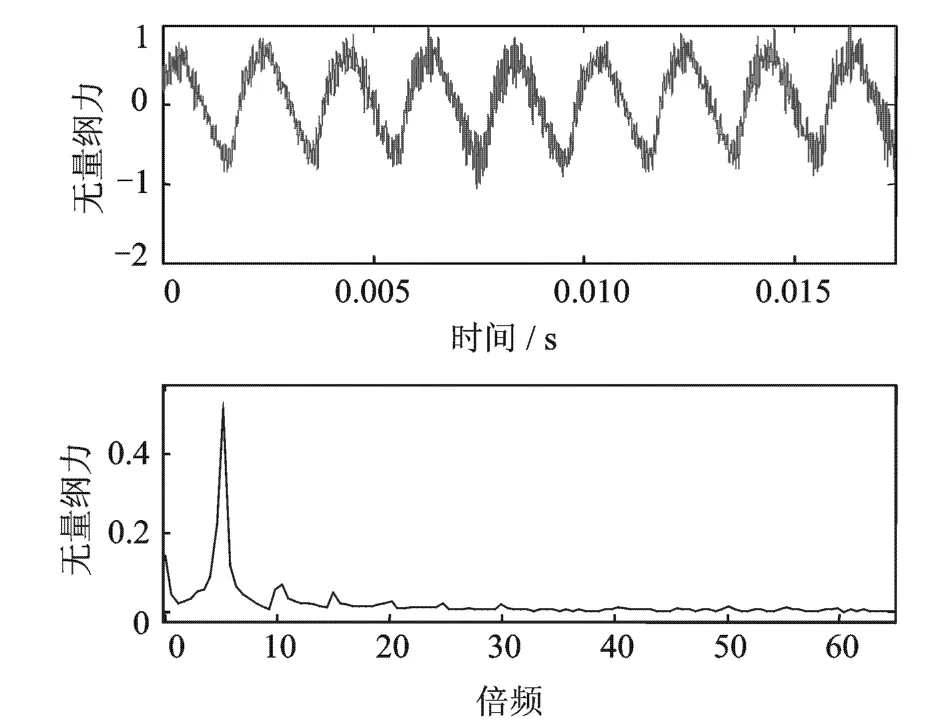
图16 无量纲化的Y向力及其频谱图Fig.16 Dimension less force in Y direction and its frequency spectrogram

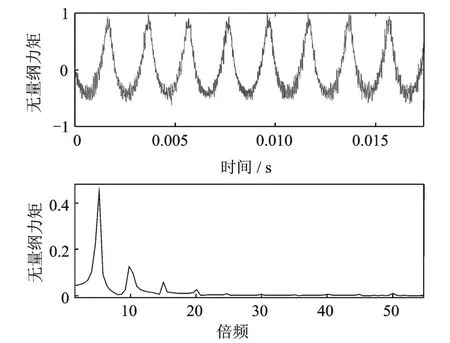
图17 无量纲化的 M Z向力及其频谱图Fig.17 Dimension less mom ent in Z direction and its frequency spectrogram

3 隔舌厚度变化对泵脉动激振力的影响分析

从上面的分析可以发现,泵叶轮所受到的流体激振力主要与离心泵叶轮叶片通过隔舌前后引起的压力脉动有关。可见,隔舌对离心泵叶轮所受到的流体激振力具有较大的影响,下面将分析隔舌的厚度对离心泵叶轮所受到的流体激振力影响。

如图18所示,通过修改离心泵中隔舌d的厚度,分别采用 CFD计算各种情况下离心泵叶轮所受到的激振力。下面分别计算了隔舌厚度d在 3.1,4.1,5.1,6.1和 7.1 mm厚度下叶轮泵所受到的脉动激振力及其频谱图。

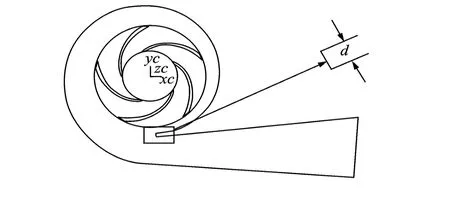
图18 泵的隔舌在截面图中的位置及厚度表示Fig.18 The position and thickness of volute tongue in the section of turbo-pump

在泵隔舌厚度d=3.1 mm情况下,泵叶轮受到的脉动激振力及其频谱图如图19和图20所示。

在离心泵隔舌厚度d=4.1mm情况下,离心泵叶轮受到的脉动激振力及其频谱图如图21和图22所示。

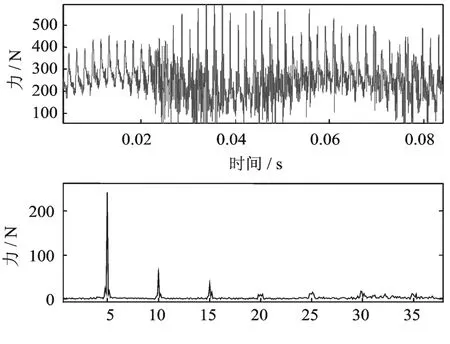
图20 Y方向激振力波形图及频谱图Fig.20 The force in Y direction and its frequency spectrogram

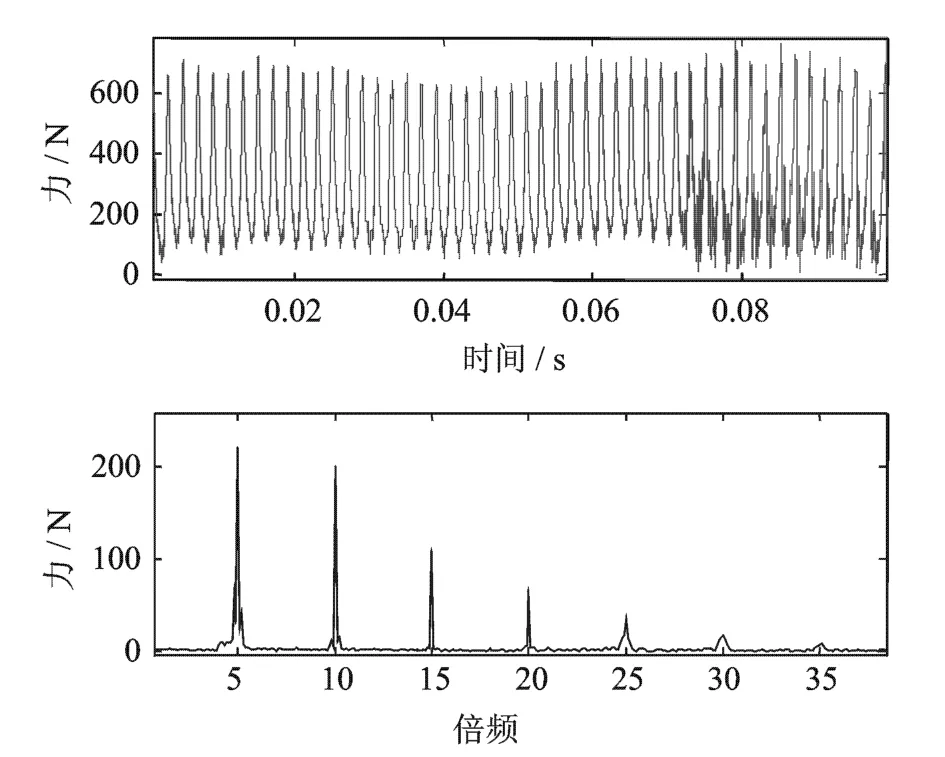
图21 X方向激振力波形图及频谱图Fig.21 The force in X direction and its frequency spectrogram

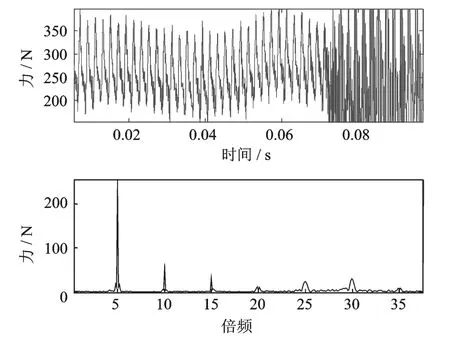
图22 Y方向激振力波形图及频谱图Fig.22 The force in Y direction and its frequency spectrogram

在离心泵隔舌厚度d=5.1mm情况下,离心泵叶轮受到的脉动激振力及其频谱图如图23和图24所示。

图23 X方向激振力波形图及频谱图Fig.23 The force in X direction and its frequency spectrogram

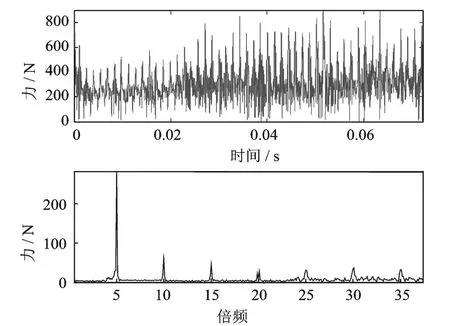
图24 Y方向激振力波形图及频谱图Fig.24 The force in Y direction and its frequency spectrogram

在泵隔舌厚度d=6.1 mm情况下,泵叶轮受到的脉动激振力及其频谱图如图25和图26所示。

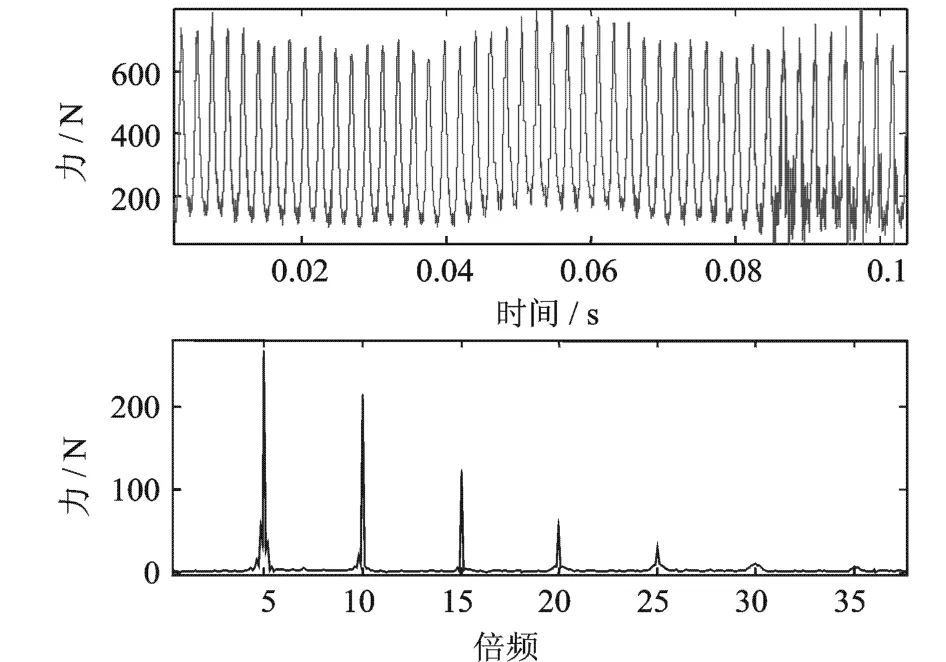
图25 X方向激振力波形图及频谱图Fig.25 The force in X direction and its frequency spectrogram

在离心泵隔舌厚度d=7.1mm情况下,离心泵叶轮受到的脉动激振力及其频谱图如图27和图28所示。

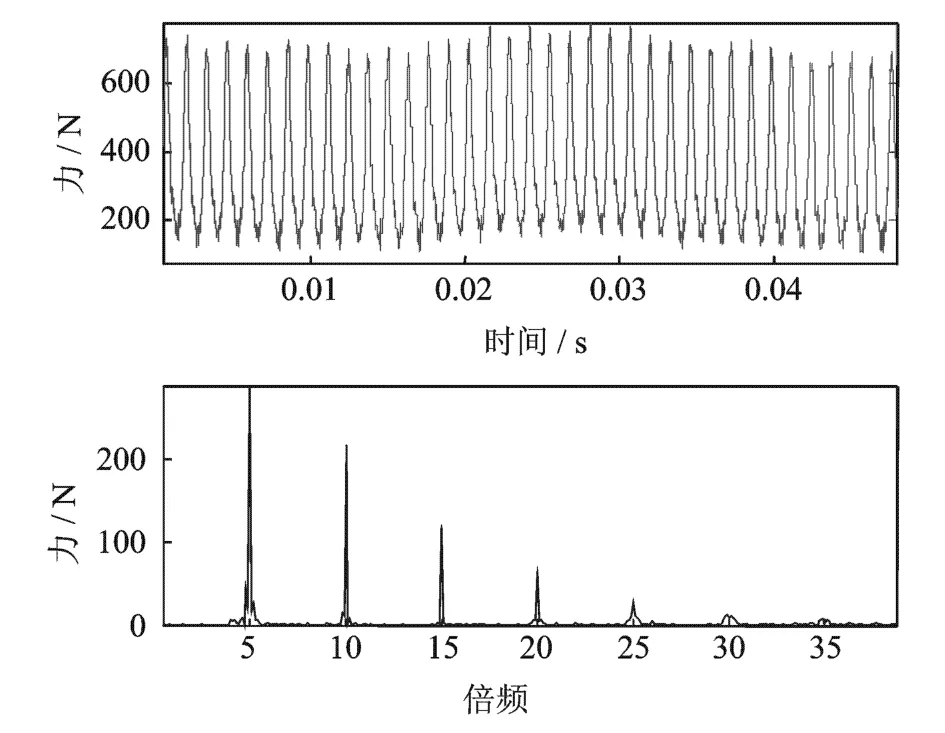
图27 X方向激振力波形图及频谱图Fig.27 The force in X direction and its frequency spectrogram

分别提取各个厚度的隔舌下离心泵叶轮所受到的 5,10,15和 20倍转频频率幅值,整理可得表1。

表1 不同厚度下X方向激振力的各倍频率幅值The amplitude of several multi-frequency of the excitation f orce on X direction under diff erent thickness of volute tongue

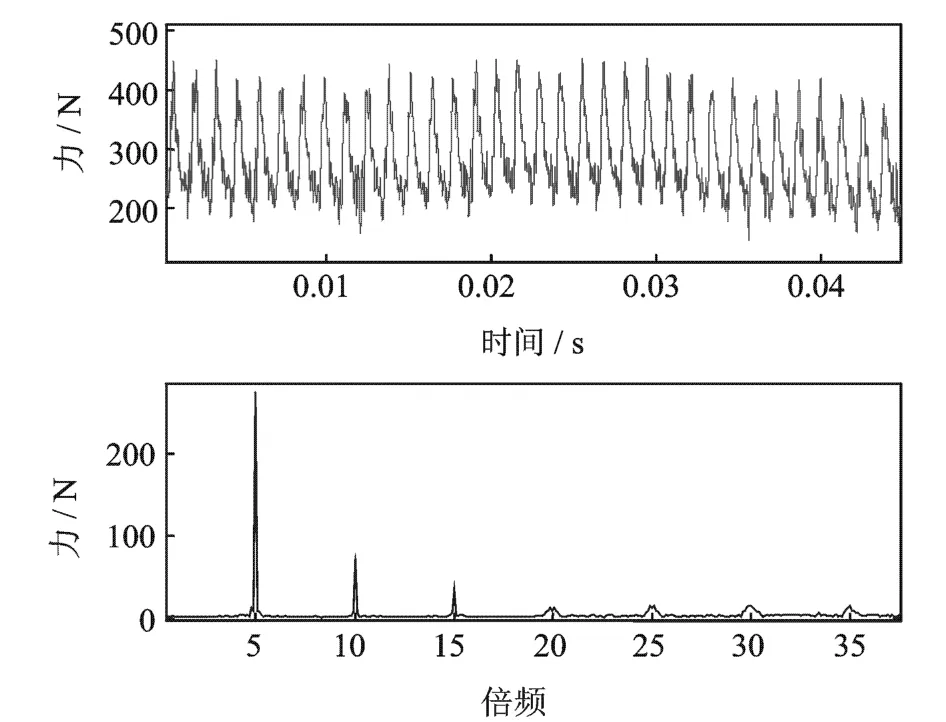
图28 Y方向激振力波形图及频谱图Fig.28 The force in Y direction and its frequency spectrogram

表1中的结果可以得到图29中各个频率成分随隔舌厚度变化的曲线。

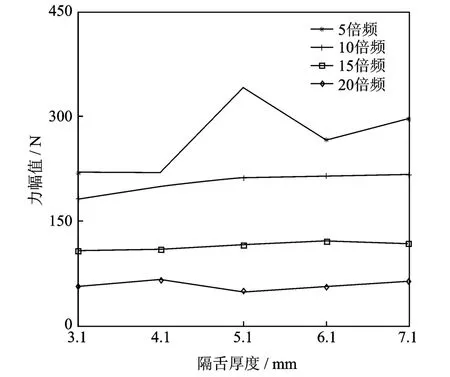
图29 不同厚度隔舌下X方向激振力叶片倍频幅值变化曲线Fig.29 The curve of the different frequency force amp litude on X direction under different vo lute tongue thickness

从表1和图29中各频率幅值随着隔舌厚度的变化曲线可以看出,随着隔舌厚度的增加,叶轮转频的5倍频,即叶片数倍频是增加的,而在隔舌厚度为 5.1 mm时,存在一个极值,这可能是由数值计算误差引起的。叶轮转频的10倍频和15倍频也是增加的,但增加量不如5倍频明显,这是由于这两个倍频的幅值较小,增加量也不是很明显。而20倍频就几乎看不出增加,这可能是由数值计算误差引起的。

同样也可以得到不同厚度隔舌下叶轮所受到的Y方向激振力的各频率成分的幅值。

表2 不同厚度下Y方向激振力的各倍频率幅值Tab.2 The amplitude of several multi-f requency of the excitation force on Y direction under diff erent thickness of volute tongue

表2中的结果可以得到图30中各个频率成分随隔舌厚度变化的曲线。

从不同隔舌厚度下Y方向激振力各倍频幅值表和变化曲线可以看出,Y方向激振力随着隔舌厚度的变化趋势与X方向是一致的。

综合X方向和Y方向的各个频率的激振力幅值随着隔舌厚度的变化趋势可以看出,随着隔舌厚度的增加,激振力是增加的。在离心泵的结构设计中,从离心泵内流动的激振力来看,离心泵隔舌厚度越小越好。

4 结 论

在设计工况下,叶轮受到的激振力与叶轮和隔舌的压力脉动有关,因此在水力及结构设计中应予以高度重视和研究;从叶轮所受的激振力的频率特征来看,叶轮受到的激振力的频率主要为叶片通过隔舌的频率,及转速的 5倍频;存在叶片通过隔舌的高倍谐波频率成分,谐波的幅值随着倍数的增加而迅速减小;流体激振力幅值随着隔舌厚度的增加而增加。

[1] Parrondo J L,Gonzá lez J,Ferná ndez J.The effect of the operating point on the pressure fluctuations at the blade passage frequency in the volute of a centrifugal pump[J].Journal of Fluids Engineering,Transactions of the ASM E,2002,124(3):784—790.

[2] Uy R V,Brennen C E.Experimental measurements of rotor dynamic forces caused by front shroud pump leakage[J].Journal of Fluids Engineering,1999,121(3):633—637.

[3] R V Uy.Studies of rotor dynamic forces generated by annular flows[D].California Institute of Technology,1998:37—42.

[4] Kitano Majidi.Numerical study of unsteady flow in a centrifugal pump[J]. Journal of Turbo machinery,Transactions of the ASME,2005,127(2):363—371.

[5] Jery B,Brennen C E,Caughey K T,et al.Forces on centrifugal pump impellers[A].Proceedings of the Second International Pump Symposium[C].Houston,TX,USA:Texas A&M University,1985:217—230.

[6] Shoji H,Ohashi H.Fluid foree on rotating centrifugal im Peller with whirling motion.Rotor dynamic instability problems in high performance turbo machinery[A].N ASA Conf.Pub.[C].College Station,TX,USA,1980:37—39.

[7] Allaire P E,Sato C J, Branagan L A. Hydraulic Force on a Centrifugal Im Peller Undergoing Synchronous Whirl.Rotor dynamic Instability Problems in High-Performance Turbo machinery[A].NASA Conf.Pub.[C].College Station,TX,USA,1984:88—100.

[8] Tsujimotor A J.A theoetical study of fluid forces on a centrifugal impeller rotating and whirling in a volute[J].Journal of Fluids and Structures,1986,52(8):3 159—3 165.

[9] 朱荣生,胡自强.双叶片泵内压力脉动的数值模拟[J].农业工程学报,2010,26(6):129—134.Zhu Rongsheng,Hu Ziqiang.Numerical simulation of pressure fluctuation in double-blade pump[J].Transactions of the CSAE,2010,26(6):129—134.

[10]王洋,代翠.离心泵内部不稳定流场压力脉动特性分析[J].农业机械学报,2010,41(3):91—95.Wang Yang,Dai Cui.Analysis on pressure fluctuation of unsteady flow in a centrifugal pump[J].Transactions of the CSAM,2010,41(3):91—95.

[11]李润泽,李琳.跨声速工况下流体诱发叶片振动研究[J].航空动力学报,2008,23(4),27—30 Li Runze,Li Lin.An investigation of flow induced blade vibrations at the transonic operating condition[J].Journal of Aerospace Power,2008,23(4),27—30.

[12]刘占生,刘全忠.离心泵变工况流场及叶轮流体激振力研究 [J].哈尔滨工程大学学报,2008,29(12):1 304—1 308.Liu Zhansheng,Liu Quanzhong.Analysis of off-design flow fields in centrifugal pumps and hydrodynamic forces on impellers[J].Journal of Harbin Engineering University,2008,29(12):1 304—1 308.