气浮式空间力矢量测量方法研究

黄 斌 余晓芬 黄 英 黄海阳 张文伟

1.合肥工业大学，合肥，230009 2.中国科学技术大学，合肥，230026

0 引言

多维力传感器主要用来测量空间力沿坐标轴的力分量和力偶分量［1－3］。有代表性的多维力传感器类型有美国Draper试验室研制的基于电阻应变片的竖梁结构 Waston六维力／力矩传感器和斯坦福大学人工智能研究所设计的横梁结构Scheinman六维力／力矩传感器［4－5］；Hirose等［6］研制的一种光学六维力传感器，采用光学测量方法测出六横梁的微小变形，从而计算出六维力。

测量精度不高是各种类型多维力传感器共同存在的一个缺憾。从已有的各种类型多维力传感器结构上看，受力体与各维测力敏感部位之间都是固体连接，难以避免各维测力敏感部位之间的联动效应，传感器测力时的测量结果包含有与被测力方向垂直的寄生力成分，即产生耦合现象。耦合与结构设计和制造过程诸多因素有关，是个很复杂的非线性问题，虽然通过解耦可以较大幅度减小维间耦合误差［7］，但无法实现完全解耦［8］。目前应用最广的电阻应变片式三维力／六维力传感器经过解耦后测量的相对误差精度只能达到1%［9－10］。

本文从如何避免多维力测量时的耦合现象角度提出了气浮式测力方法［11－12］。用气浮式测力方法测量三维力，受力体依靠气体产生的浮力而悬浮平衡，各个测力敏感部位之间不存在固体连接，因而不存在维间耦合现象，可较大幅度地提高多维力的测量精度。

1 一维气浮测力模型

气浮测力需要设置喷嘴－浮板机构，通过测量喷嘴－浮板机构中特定部位的压力、流量、流速等气流参数，来求得作用在浮动体上外力的大小。本文研究的一维气浮测力模型如图1所示，它包括浮板、主喷嘴、承压腔、测压口和横向喷嘴等部分。浮板底面与侧面垂直，主喷嘴与横向喷嘴垂直，各喷嘴分别正对浮板底面和侧面。具有一定压力的气流经主喷嘴流入主喷嘴与浮板之间的承压腔和缝隙，在主喷嘴和浮板底面之间形成气垫，浮起浮板；横向喷嘴对称布置在浮板的侧面，具有一定压力的气流经横向喷嘴，在横向喷嘴与浮板侧面之间形成气垫，使浮板横向保持平衡。该模型实质是一个由主喷嘴和浮板组成的喷嘴－浮板机构，横向喷嘴只起横向稳定浮板的作用。建立的直角坐标系如图1所示，主喷嘴对浮板产生的浮力沿Y方向，横向喷嘴对浮板产生的浮力沿X方向。通过测量承压腔中的气体压力，可求出作用在浮板上的外力在Y方向上分量的大小。根据流体承载的特性，承压腔与浮板之间的气垫只能承受正压力而不能承受剪切力，横向力对测量结果不会形成干扰。

图1中，设气浮喷嘴和浮板为圆形，r1为承压腔半径，r2为主喷嘴半径，h为喷嘴与浮板之间的气膜厚度，pd为承压腔内的气体压力，pa为周边环境气压，pc为横向喷嘴的供气压力，F为作用在浮板上的外力沿Y方向的分量，v为喷嘴与浮板之间沿半径方向的气体流动速度。在建立F与pd之间数学模型时可假设［13］：由加速度引起的惯性力同黏性剪切机理引起的摩擦力相比可忽略不计；气膜中的气体流动为层流；垂直于气流的截面上的压力是恒定的；在流体与板之间的界面上不存在滑动。根据诺维—斯多克斯方程，距离喷嘴中心r处，有

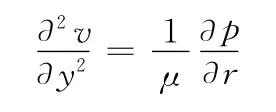
式中，μ为气体的动力黏度；p为气体压力。

对上式积分，并注意到当y＝0，y＝h时，v＝0，可得

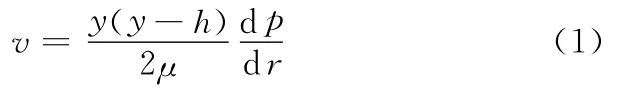
设气体的密度为ρ，则流过半径r、气膜厚度为h的环流面积的质量流量qm为

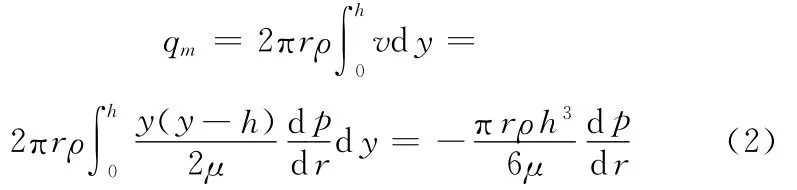
由式（2）得

假定气流不可压缩，处于半径r（r1≤r≤r2）处的缝隙中的气体压力可通过对式（3）积分得到：

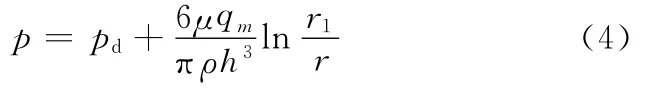
当r＝r2时，p＝pa，所以有

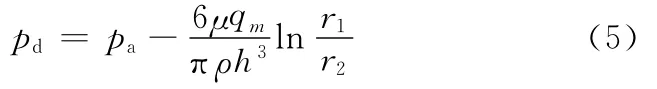
将式（5）代入式（4）得

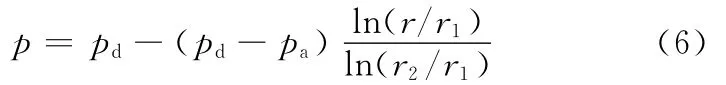
一维气浮测力模型的承载力F为

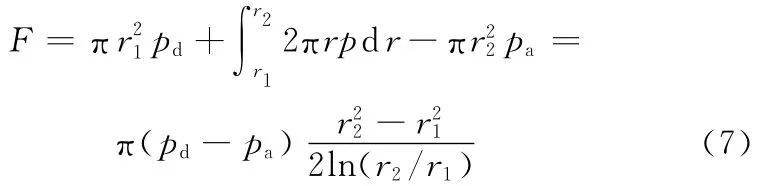
式（7）说明，对于给定的一维气浮测力模型，承载力F只与喷嘴—浮板机构中气体承压腔内的气体压力pd有关，通过测量pd可以求得F的大小。

2 三维力矢量气浮式测量模型

2.1 三维力矢量气浮式测量原理

根据力的分解与合成原理，在某个三维直角坐标系OXYZ中，任意一个力矢量F可以向坐标原点O简化，得到一个主矢和一个主矩。如图2所示，在直角坐标系OXYZ中，设有力矢量F，F通过空间某一点（x，y，z），则F简化到O 点的主矢FO和主矩MO分别为

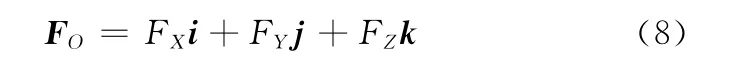
式中，FX、FY、FZ分别为力矢量F 沿坐标轴X、Y、Z的分量；MX、MY、MZ分 别 为 主 矩 MO沿 坐 标 轴 X、Y、Z 的分量。

由式（8）、式（9）可知，通过测量出力矢量F沿三个坐标轴的分力以及绕三个坐标轴的力矩可以求出矢量F。

力矢量的气浮式测量模型如图3所示：用16个结构相同的气浮喷嘴将一块矩形六面体结构的浮板完全浮起，每个喷嘴正对浮板，形成一个一维气浮—浮板机构。以浮板几何中心为原点建立三维直角坐标系OXYZ，其中，X轴垂直于浮板左右侧面，Y轴垂直于浮板的前后侧面，Z轴垂直于浮板的上下面。喷嘴按2个一组相对、共线布置的方式对称布置在浮板的左右两侧面、前后两侧面和上下两表面。浮板的前后面布置2组喷嘴，左右面布置2组喷嘴，上下面布置4组喷嘴。图3中，箭头表示气浮喷嘴布置方向，即喷嘴产生的气体压力的方向，其中，正对浮板前后侧面布置的2组喷嘴在OXY平面内，喷嘴中心到X轴的距离为l；正对浮板左右侧面布置的2组喷嘴在OXY平面内，喷嘴中心到Y轴的距离为l；正对浮板上下侧面布置的4组喷嘴中心到X轴和Y轴的距离均为l。通过差动测量各组喷嘴中两个气浮承压腔内的气体压力差值可求取作用在浮板上力矢量F沿X、Y、Z轴的3个分力和绕X、Y、Z轴的3个力矩。

2.2 三维力矢量的求取

在图3所示的力矢量气浮式测量模型中，通过浮板中心建立的坐标系OXYZ如图3所示。设浮板4个拐角处的浮力的交汇点分别为A、B、C、D，且各点坐标分别为 A（l，－l，0）、B（l，l，0）、C（－l，－l，0）、D（－l，l，0）；记通过A点、C点且沿X方向布置的一组喷嘴差动测量得出的力为FCA，FCA方向由C指向A为正；通过D点、B点且沿X方向布置的一组喷嘴差动测量得出的力为FDB，FDB方向由D指向B为正；通过A点、B点且沿Y方向布置的一组喷嘴差动测量得出的力为FAB，FAB方向由A指向B为正；通过C点、D点且沿Y方向布置的一组喷嘴差动测量得出的力为FCD，FCD方向由C指向D为正；正对浮板上下表面布置的每组气浮测力喷嘴测量得出的沿Z轴正方向的力分别为FAZ、FBZ、FCZ、FDZ。于是，在X、Y、Z轴方向上测出的力FX、FY、FZ为

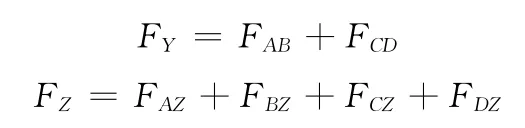
设作用在浮板上某点的外力为R，R沿X、Y、Z轴的3个分力和绕X、Y、Z轴的3个力矩分别记为RX、RY、RZ以及M′X、M′Y、M′Z，FCA、FDB、FAB、FCD绕Z 轴转动的力臂为l，FAZ、FBZ、FCZ、FDZ绕X轴和Y轴转动的力臂均为l，则有

R的大小以及与X、Y、Z坐标轴正向夹角α、β、γ的方向余弦分别为

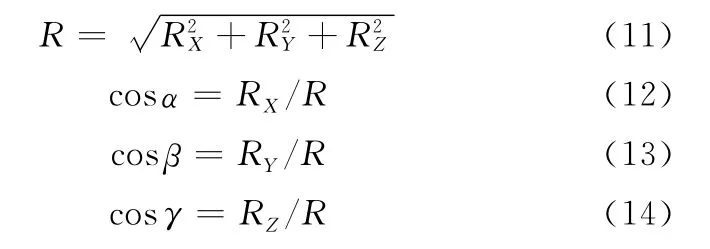
设浮板表面在OXYZ坐标系中的方程是z＝z0，若R在X、Y、Z方向上的分力均不为零，作用在浮板表面的作用点坐标是（x0，y0，z0），则有

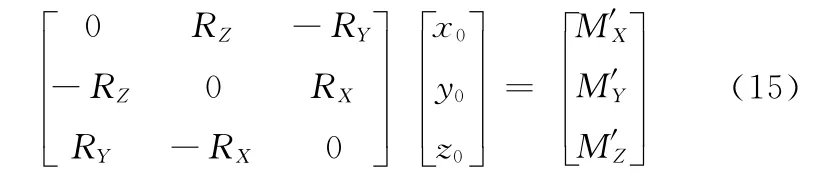
解式（15）可解得

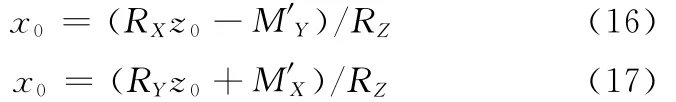
若R作用在浮板表面上，即R在Z轴方向上的分力RZ为零，但在X、Y方向上的分力RX、RY不为零，则R与OXZ平面的交点坐标（x0，z0）由下式求出：

R与OYZ平面的交点坐标（y0，z0）由下式求出：

若R作用在浮板表面上且与X轴平行，则R偏离Z轴的距离可由式（20）求出；若R作用在浮板表面上且与Y轴平行，则R偏离Z轴的距离可由式（18）求出。

3 实验验证

根据力矢量气浮式测量模型研制的气浮式力矢量测量平台如图4所示。在气浮式力矢量测量平台的浮板上加载已知的力矢量，直接测出的是各组气浮承压腔内的气体压力差值，由式（10）～式（21）可以得出作用在浮板上的力矢量的测量值。在研制的气浮式力矢量测量平台上进行了实验，实验过程中，各组加载力的大小、方向和作用点的坐标如表1所示。考虑到气浮式力矢量测量平台在X方向和Y方向具有完全对称的结构，沿坐标轴加载实验只需沿X方向和Z方向进行。加载点选择在浮板表面不同的位置；根据所研制的气浮式力矢量测量平台具体结构尺寸，浮板表面在图3所示的坐标系中的方程为z＝10mm。

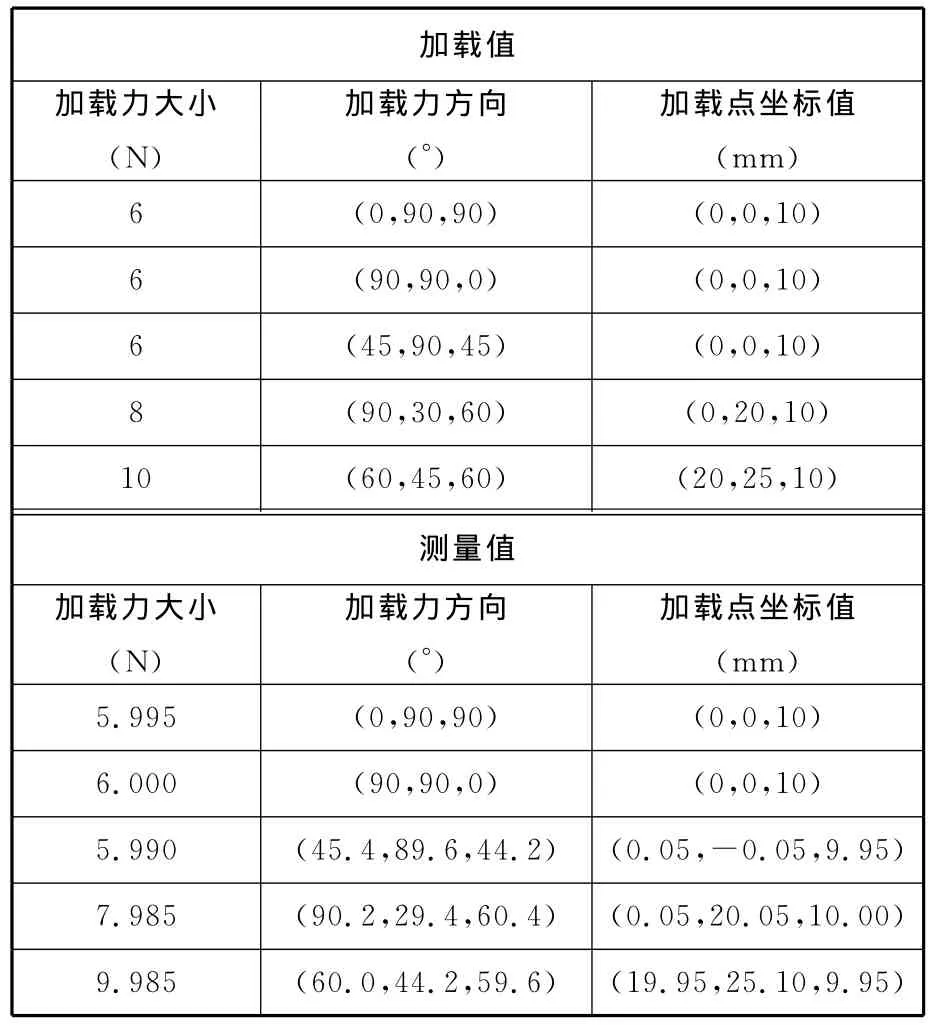
表1 气浮式测力平台加载方向及加载点实验

分析实验数据可得：沿坐标轴方向加载时，其他坐标轴方向测量值均为零，这表明气浮式测力平台测力时不存在维间耦合现象，符合理论预期。空间力矢量测量的误差如下：力的相对误差为0.2%，力的方向误差为0.5°，力的作用点坐标值误差为±0.05mm。

4 结语

提出了一种基于气浮测力原理的三维空间里任意力矢量的精密测量方法，设计了一种测量力矢量的气浮式测力平台模型，推导得出了作用在气浮式测力平台上力矢量的计算公式；研制了力矢量的气浮式测力平台样机，通过实验得出，气浮式测力平台测力时不存在维间耦合。空间力矢量测量的相对误差如下：力的大小误差为0.2%，力的方向误差为0.5°，力的作用点坐标值误差为±0.05mm。

［1］唐毅.SAFMS－T六维力测力平台及应用问题研究［D］.合肥：中国科学院合肥智能机械研究所，2001.

［2］崔勇.Stewart平台六维力传感器及其标定系统的设计［D］.秦皇岛：燕山大学，2006.

［3］贾振元，李映君，张军，等.并联式轴用压电六维力／力矩传感器［J］.机械工程学报，2010，46（1）：62－67.

［4］黄惟一，王玉生，薛亚洪.机器人腕力传感器的发展［J］.机器人技术，1987（1）：1－3.

［5］张福学.智能机器人传感技术.北京：电子工业出版社，1996.

［6］Hirose S，Yoneda K.Development of Optical 6－axial Force Sensor and It’s Signal Calibration Considering Nonlinear Interference［J］.Robotics and Automation，1990，1（7）：46－53.

［7］徐科军，李成.多维力传感器迭代动态解耦方法［J］.中国机械工程，1999，10（1）：46－48.

［8］蒲筠果，赵晓东.机器人力传感器分析［J］.邢台职业技术学院学报，2004，21（5）：21－15.

［9］王国泰，易秀芳，王理丽.六维力传感器发展中的几个问题［J］.机器人，1997，19（6）：474－478.

［10］郑红梅，刘正士，郑传荣，等.机器人六维腕力传感器标定试验台误差分析与研究［J］.计量学报，2005，26（4）：333－336.

［11］合肥工业大学.气浮式多维力传感器及多维力测量方法：中国，ZL200810019550.2［P］.2010－07－25.

［12］合肥工业大学.力及位移量的气浮式测量方法：中国，ZL200810020468.1［P］.2010－03－24.

［13］Powell J W.空气静压轴承设计［M］.丁维刚，等，译.北京：国防工业出版社，1978.