高心墙堆石坝初次蓄水速率影响研究

王年香，章为民，张 丹，顾行文

（1.南京水利科学研究院 岩土工程研究所，江苏 南京210024；2.中国水电顾问集团成都勘测设计研究院，四川 成都610072）

0 引言

四川大渡河长河坝水电站工程为一等大（1）型工程，挡水、泄洪、引水及发电等永久性主要建筑物为1级建筑物，拦河大坝采用砾石土心墙堆石坝，最大坝高240 m，上、下游坝坡均为1∶2.0.心墙上、下游坡均为1∶0.25，与上、下游坝壳堆石之间均设有反滤层、过渡层.坝址河床覆盖层深达65～76.5 m，坝基采取全封闭主、副两道防渗墙防渗，分别厚1.4 m和1.2 m，净距14 m，墙底嵌入基岩1.5 m.在初期导流洞及中期导流洞封堵后，因水库水位未达到上层泄水建筑物底板高程，且长河坝工程为大流量河流上的狭谷型水库，水库水位上升速率可能高达20～30 m／d.设计非常关注对于如此快的水位上升速率，心墙是否会发生水力劈裂破坏？大坝允许最大水位上升速率是多少？

1 土石坝心墙水力劈裂研究

1976年美国Teton坝在蓄水初期突然失事［1］，被确认是由于水力劈裂引起的大坝渗漏破坏以来，水力劈裂的问题得到了广泛关注［2］，关于水力劈裂的研究也逐渐增多.为了弄清水力劈裂机理，人们进行了大量的现场、室内试验［3］、数值模拟［4］.但由于水力劈裂的发生条件尚未完全弄清，导致试验研究成果直接用于工程实践尚有一段距离.

朱俊高等［5－6］认为心墙材料的低透水性与心墙存在局部裂缝或缺陷是发生水力劈裂的物质条件，而足够大的所谓“水楔”作用是其发生的力学条件.图1是存在水平裂缝（其他具有与心墙上游面相交裂缝的情况与此类似）的心墙的水力劈裂情况.当库水位达到或高于裂缝时，水体进入裂缝，裂缝表面作用水压力p1，裂缝附近土体作用水压力p2.当库水位缓慢上升时，进入裂缝中的水体有足够的时间向裂缝两边的土体渗透并形成稳定渗流，p1＝p2，那么所谓的“水楔”作用将无法形成.另外，由于裂缝两侧土体可能会遇水膨胀使裂缝封闭，即发生所谓的“湿封”现象，“水楔”作用无法形成，水力劈裂也就不会发生.当库水位的上升速率较快，p1远大于p2，稳定渗流无法形成，内外水压力差（p1－p2）随库水位的升高而迅速增大，当其大到足以克服裂缝扩展阻力时，裂缝就扩展，水体随即进入新的裂缝，水压力也作用于新的裂缝面，如果该水压力仍大于当前裂缝的扩展阻力，裂缝继续扩展，直到水压力不再大于当前裂缝扩展阻力为止.如果库水位继续上升，作用于裂缝面使裂缝扩展的水压力增大，裂缝将进一步扩展，最终可能形成贯穿心墙的裂缝，导致心墙发生集中渗漏，进一步可能导致溃坝事故.因此，裂缝是否扩展将决定于“水楔”作用与裂缝抗扩展能力的关系.

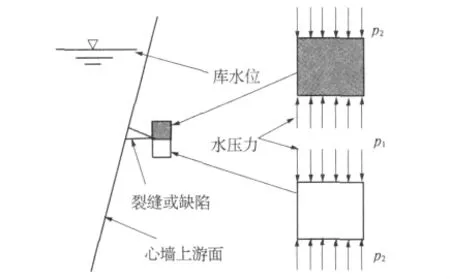
图1 心墙的水力劈裂情况Fig.1 Hydraulic fracturing in the core

土工离心模型试验技术是用原型材料制作模型，在原型应力状态下，对研究对象的受力变形状况和破坏过程进行直观研究的试验方法，在岩土工程的许多领域都得到应用［7－8］.沈珠江等［9］进行了模拟Teton坝破坏过程的离心模型试验，结果表明心墙没有发生水力劈裂，这与1976年美国Teton坝在蓄水初期突然失事的原因分析完全不同.模型心墙是均质的，并不包含预制的裂缝或缺陷，即水力劈裂发生所需的物质条件并不完全具备，“水楔”作用无法形成，水力劈裂现象也就不可能发生.冯晓莹等［10］简化心墙的受力条件，进行了直立土柱离心模型试验，试验中上游水头高于土柱高度，以研究心墙水力劈裂机理.该试验同样只注重水力劈裂的力学条件，而未考虑物质条件.

2 试验方法

采用长高宽为1 000 mm×1 000 mm×400 mm的模型箱，取最大断面、按平面问题进行试验，模型比尺取为240，模拟240 m坝高，试验模型布置见图2.试验模拟了心墙料和堆石料两种筑坝材料.心墙料试验采用的限制粒径取为10 mm，按等量替代法确定模型心墙料的颗粒级配.堆石料试验采用的限制粒径取为20 mm，先按相似级配法进行缩尺，再按等量替代法确定模型堆石料的颗粒级配.心墙料分为两个区，高程1 585 m以上为心墙Ⅱ区，为新莲心墙料，干密度为2.14 g／c m3，相应含水率为10.5%；高程1 585 m以下为心墙Ⅰ区，为汤坝心墙料，干密度为2.07 g／c m3，相应含水率为10.6%.堆石料采用花岗岩，控制相对密度定为0.9，填筑密度为2.18 g／c m3.采用分层方法填筑心墙料和堆石料，每层压实后的层厚为5 c m.

心墙裂缝的模拟.设想心墙在高程1 590 m和1 510 m两处有裂缝，裂缝顺河向深入心墙5 m，沿坝轴向长度10 m.心墙中裂缝或缺陷宽度都比较小，一般只有微米量级，最多也就1～2 mm，这样再除于模型比尺240，就相当薄，在制作模型时不可能在心墙中预留这样薄的裂缝或缺陷.考虑到本项试验心墙中裂缝或缺陷是与库水位相通的，其作用是把蓄水水压力引到心墙裂缝中，因此，试验采用排水板滤膜来模拟裂缝，滤膜厚度为0.1 mm，滤膜顺河向深入心墙21 mm，沿坝轴向长度42 mm，布置在模型箱的有机玻璃面处，布置位置见图2.

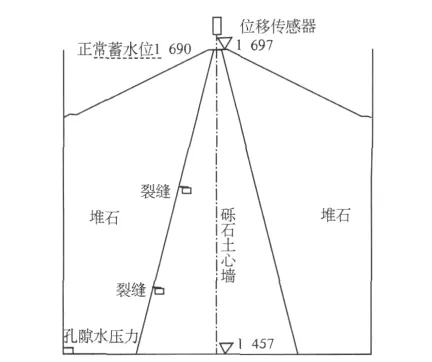
图2 模型试验布置图Fig.2 Layout of the model

试验模型布置了位移传感器和孔隙水压力传感器，具体布置如图2所示.在坝顶中心处安装位移传感器，测定蓄水水位上升速率对心墙沉降的影响.在两条裂缝下方10 mm处（相当于原型2.5 m）埋设孔隙水压力传感器，测定不同蓄水水位上升速率时心墙的孔隙水压力，即图1中的p2，而心墙裂缝中的水压力p1即为库水压力，是已知的.在模型箱底（相当于原型1 457 m高程处）埋设孔隙水压力传感器，测定蓄水水位上升速率.

蓄水水位上升速率的模拟.在离心机上安装水箱和3个电磁阀，通过反复试验，控制电磁阀的流量，达到模拟3种蓄水水位上升速率（20，10和5 m／d）的要求，在正式试验中采用.考虑水库初次蓄水3种蓄水水位上升速率（20，10和5 m／d），研究施工期水位上升速率的影响.在离心机加速度达240 g后即开通电磁阀向上游放水，模拟蓄水，蓄水水位高程为1 690 m.

试验模拟了大坝的施工期和20 a运行期.在离心机加速上升过程中，根据大坝的施工速率，来控制离心机加速度的上升速率，以模拟大坝施工期.然后保持离心机在设计加速度（240 g）下运行，以模拟大坝20 a运行期.

3 裂缝附近水压力分析

在裂缝下面2.5 m处埋设孔隙水压力传感器，以测定蓄水水位上升过程和运行期心墙裂缝下面2.5 m处水压力（即图1中的p2）的变化情况.图3为不同蓄水水位上升速率情况时孔隙水压力上升阶段的过程线，其中无点线为裂缝处的静水压力，比较裂缝处静水压力和裂缝下面2.5 m处孔隙水压力可以看出，裂缝下面2.5 m处孔隙水压力比裂缝处静水压力启动和稳定均要延迟.表1列出了不同蓄水水位上升速率时裂缝下面2.5 m处孔隙水压力和裂缝处静水压力的启动时间、稳定时间、启动时差、稳定时差、承压时间，随着蓄水水位上升速率的加快，启动时差稍有增加，稳定时差显著增加，承压时间有所延长.

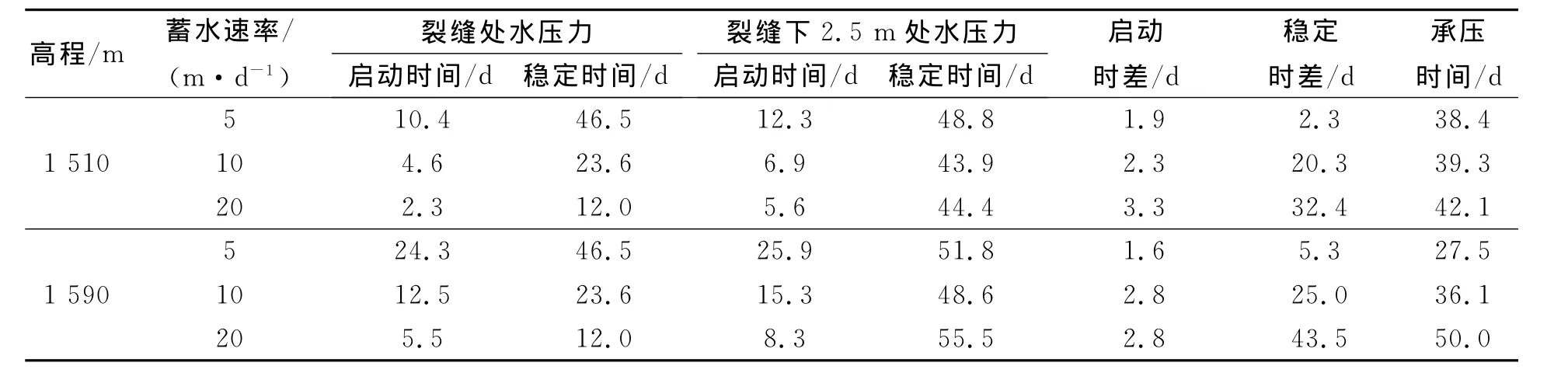
表1 裂缝附近水压力特征时间Tab.1 Characteristic time of water pressure of core near cr ack

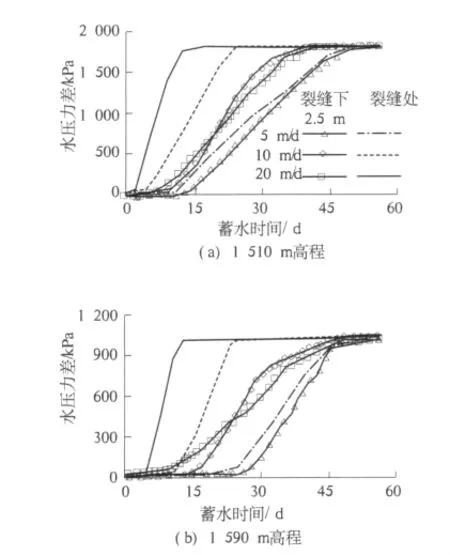
图3 裂缝附近水压力上升过程线Fig.3 Water pressure－time curves of core near crack

承压时间是引起水力劈裂的一个因素，而压差更是引起水力劈裂的重要因素.图4为不同蓄水水位上升速率时孔隙水压力差（裂缝处静水压力与裂缝下面2.5 m处孔隙水压力之差）（即图1中的p1－p2）过程线，可以看出，蓄水水位上升速率越快，孔隙水压力差增长越快，峰值越大，持续时间越短，而后下降也越快；蓄水水位上升速率越慢，孔隙水压力差增长越慢，峰值越小，持续时间越长，而后下降也越慢.

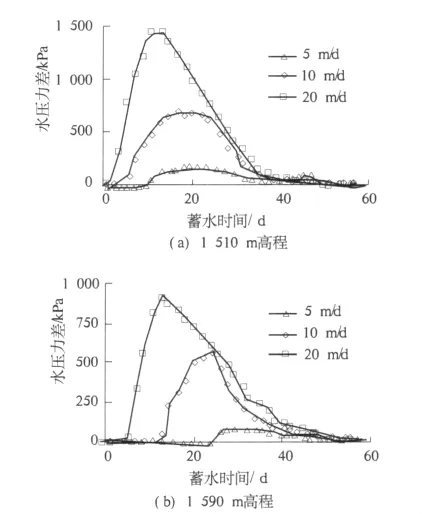
图4 裂缝附近水压力差过程线Fig.4 Difference of water pressure－time curves of core near crack

4 大坝允许最大蓄水速率分析

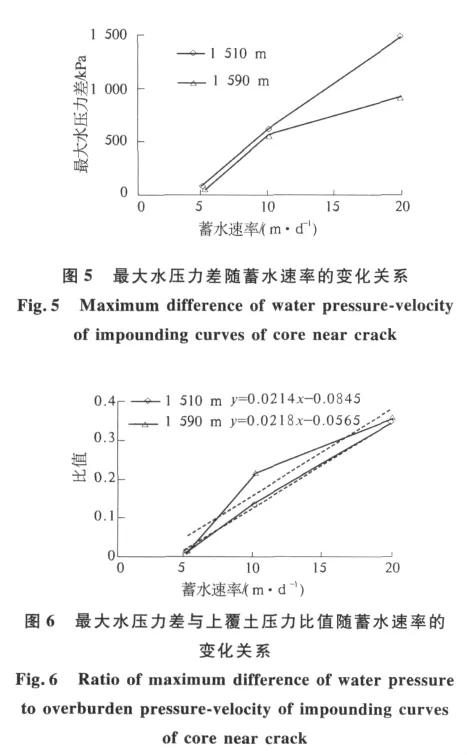
“水楔”作用是引起水力劈裂的力学因素，从图1可以看出，心墙裂缝中水压力p1与附近土体水压力p2之差即为“水楔”作用.图5为最大水压力差（裂缝处静水压力与裂缝下面2.5 m处水压力之差的最大值）随蓄水水位上升速率的变化关系，可以看出，蓄水水位上升速率越快，最大水压力差越大.如果说从最大水压力差还不太好分析心墙是否发生水力劈裂的话，那么从最大水压力差与上覆土压力之比就可看出端倪，图6为最大水压力差与上覆土压力之比随蓄水水位上升速率的变化关系，比值随蓄水速率几乎是线性增大，且不同高程处的基本平行.由于水压力各个方向是相等的，而水平向土压力一般小于竖向土压力，其大小取决于土压力系数，这就是说，如果最大水压力差与上覆土压力比值大于土压力系数的话，最大水压力差就大于水平向土压力，就可能发生水力劈裂，因此，这比值应小于土压力系数.一般土压力系数按0.5取值，根据图6的线性回归线，就可以计算出大坝允许最大蓄水速率，1 510 m高程处允许最大蓄水速率为27.3 m／d，1 590 m高程处允许最大蓄水速率为25.5 m／d.因此，从最大水压力差分析得出大坝允许最大蓄水速率为25.5 m／d.

表2 不同蓄水水位上升速率时水压力差峰值及其与上覆土压力之比Tab.2 Maximum difference of water pressure and its ratio to overburden pressure of core near crack under different velocity of i mpounding

5 结论

（1）在蓄水速率不大于20 m／d条件下，蓄水水位没有出现快速下降现象，表明裂缝未贯穿整个心墙，心墙没有出现水力劈裂问题.

（2）裂缝下面2.5 m处水压力比裂缝处静水压力启动和稳定均要延迟.随着蓄水水位上升速率的加快，启动时差稍有增加，稳定时差显著增加，承压时间有所延长.

（3）蓄水水位上升速率越快，水压力差增长越快，峰值越大，持续时间越短，而后下降也越快.

（4）从心墙水压力差分析得出大坝允许最大蓄水速率为25.5 m／d.

［1］ SEED H B，DUNCAN J M.The Teton Dam failure－A retrospective review［C］／／In：the Proc.10th ICSMFE.Stockhol m，1981：219－239.

［2］ 张丙印，于玉贞，张建民.高土石坝的若干关键技术问题［C］／／中国土木工程学会第九届土力学及岩土工程学术会议论文集.北京：清华大学出版社，2003：163－186.

［3］ 孙亚平.水力劈裂机理研究［D］.北京：清华大学水利系，1985.

［4］ 李全明，张丙印，于玉贞，等.土石坝水力劈裂发生过程的有限元数值模拟［J］.岩土工程学报，2007，29（2）：212－217.

［5］ 朱俊高，王俊杰，张辉.土石坝心墙水力劈裂机制研究［J］.岩土力学，2007，28（3）：487－492.

［6］ 王俊杰，朱俊高，张辉.关于土石坝心墙水力劈裂研究的一些思考［J］.岩石力学与工程学报，2005，24（增2）：5664－5668.

［7］ 南京水利科学研究院土工研究所.土工试验技术手册［M］.北京：人民交通出版社，2003.

［8］ 王年香，章为民.离心模型试验技术在岩土工程中的应用［C］／／中国水利水电工程未来与发展.大连：大连理工大学出版社，2002.

［9］ 沈珠江，易进栋，左元明.土坝水力劈裂的离心模型试验及其分析［J］.水利学报，1994（9）：67－78.

［10］冯晓莹，徐泽平，栾茂田.黏土心墙水力劈裂机理的离心模型试验及数值分析［J］.水利学报，2009，40（1）：109－114.