基桩缺陷定量识别研究

杜思义，宋世波

（郑州大学 土木工程学院，河南 郑州450001）

0 引言

随着我国建筑业的迅速发展，桩基工程越来越多，基桩在施工过程中，由于地质条件和工艺的影响，桩身经常存在缺陷.桩基属隐蔽工程，为了确保建筑物的安全，必须进行基桩质量检测，目前，在基桩完整性的动力检测方法中，应力波反射法使用最为普遍，其利用应力波在传播过程中遇到截面阻抗变化而产生反射和透射的原理识别桩身完整性，如判别桩的长度、桩身缺陷以及缺陷的位置等，但这种方法还存在很多问题不能解决，如不能对缺陷程度准确定量，不能识别桩身阻抗的缓慢变化和整体老化等［1－2］.

目前，能定量识别基桩缺陷的方法主要是高应变方法，这种方法要使用大型设备，做起来很慢，而且费用很高，不能对基桩进行普遍检测.近几年，研究较多的是低应变方法，如低应变曲线拟合法，WANG－PIP法等［3］.这些方法未能准确考虑桩土作用对桩轴向振动的影响，分析得出的结果存在较大的误差［4］.作者试图考虑桩周土体对桩的作用，并将摄动理论应用到基桩缺陷的定量识别上，定义基桩的损伤识别单元及损伤识别参数，建立桩身损伤识别模型以及桩周土的约束模型.然后利用结构振动理论和有限元方法［5］，根据桩损伤前后的固有频率的变化，确定基桩的缺陷位置和缺陷程度.

1 基桩振动的力学模型

1.1 基本假设

① 桩周土为均质土，各向同性的线性黏弹性体，材料阻尼是黏性阻尼；② 桩身为有限长的等截面均质直杆，桩身材料阻尼忽略不计；③ 桩－土系统振动为小变形，属于线性振动；④ 因为研究对象是基桩的轴向振动频率，所以假设桩振动只发生轴向位移，径向位移忽略不计，桩底部为弹性支承.

1.2 基桩的力学模型

采用有限单元方法，将基桩分成n个单元［6］，桩周土对桩的作用效应可以简化为分布的Voigt体，线性弹簧模拟的是桩周土对桩的轴向弹性作用，线性阻尼器模拟的是桩周土对桩身的阻尼效应；考虑到桩底土对桩的弹性作用，桩处于端承桩和摩檫桩之间，桩底土的弹性作用也可以用一个Voigt体表示.因此基桩的轴向振动的力学模型如图1所示.

2 基桩缺陷的损伤识别

2.1 基桩的几何物理参数

基桩的整体刚度、质量、阻尼矩阵是由相应的单元矩阵组装而成的.设基桩离散成n个单元，则有n＋1个结点，桩为均质直杆.这n个有限单元即作为损伤识别单元.

图1 基桩的力学模型Fig.1 The mechanical model of fondation pile

（1）整体刚度矩阵.根据《动力机器基础设计规范》得到桩尖土的抗压刚度系数的表达式为

式中：A为桩端位置处的横截面面积；Cz为桩端土的当量抗压刚度系数.

NOVAK［9］等根据弹性动力学理论推出了桩侧土的刚度系数为

式中：Gi为桩周土的剪切模量.

桩侧土对桩的弹性作用可以等效成一个弹簧作用到桩身单元上的，运用有限元的结点等效原理，将弹簧转换作用到单元结点上，则桩侧土对桩的弹性作用可表示为

将桩底土对桩的弹性作用（kd）和桩侧土对桩的弹性作用（kt）组集到整体刚度矩阵中，得到考虑桩底土和桩侧土对桩弹性作用的整体刚度矩阵：

（2）整体质量矩阵.单元的质量矩阵：Me＝组集单元质量矩阵得到桩身的整体质量矩阵为

（3）整体阻尼矩阵.NOVAK［9］等根据弹性动力学理论导出桩侧土对桩的阻尼系数cti＝2πr0LYSMER和 RICHARD［10］根据弹性半空间理论推导出桩端土阻尼系数的表达式cd＝3.其中：Gi为桩周土的剪切模量，ρi为桩周土的密度，组集得到整体阻尼矩阵.

计算时可以将桩侧土的阻尼转化为比例阻尼.

2.2 损伤识别参数的确定

根据基桩常见缺陷，基桩的损伤识别参数可认为是桩的横截面A或弹性模量E的变化率，若桩身横截面的改变，可以同时引起刚度矩阵和质量矩阵的变化，通过单元刚度矩阵和质量矩阵的表达式可以看出它们都是横截面A的线性函数，可以假设两者具有相同的变化率εj，若桩在第j个单元存在缺陷，横截面A的变化率为即：

则第j个单元的损伤后的单元刚度矩阵为

第j个单元的损伤后的质量刚度矩阵为

假如桩身横截面没有发生变化，而是桩身的弹性模量E发生变化，则只有刚度矩阵发生变化，质量矩阵没有变化，即，若桩在第j个单元存在缺陷，弹性模量E的变化率为εj，即：

则第j个单元的损伤后的单元刚度矩阵为

2.3 基桩损伤识别的算法

根据矩阵摄动理论，可将系统的振动特征值按小参数ε展成Taylor级数，忽略3阶以上小量，可写为

式中：s表示系统特征值和特征向量的阶数；λs1j，λs2ij分别为特征值和特征向量的1阶摄动和2阶摄动

根据文献［8］所述，仅用1阶摄动进行识别就能得出满意的结果，因此由式（12）简化得特征值1阶摄动公式：

运用优化方法求桩的损伤识别参数，用矩阵表示写成线性规划形式如下.

另外，根据文献［8］，上述损伤识别方程也可以采用筛选法求解.求解上述方程可以得到桩损伤识别参数ε，εj值表示损伤程度的大小，脚标j表示损伤识别单元的位置.

3 模型桩损伤识别实验

桩，模型桩为方形，截面积为0.15 m×0.15 m，桩长1.5 m.弹性模量为2.55×104MPa，混凝土密度为2 450 kg·m－3桩身混凝土强度等级为C20，砼配合比：水∶水泥∶砂∶石子＝0.43∶1∶1.90∶3.63，桩身配筋为4Φ10.模型桩混凝土浇注后养护28 d，然后进行实验.桩的损伤情况设置如表1所示.

表1 桩的损伤工况表Tab.1 The table of piles defect conditions

损伤模拟的方法：首先找好单元的位置，用钢锯在损伤单元的位置处，在损伤的单元位置处的4个表面分别锯上0.05 m深的损伤，每隔0.01 m锯上一道，这样可以近似的认为只有单元的刚度改变了，而质量矩阵没有改变.

实验在郑州大学结构实验室进行，信号采集采用DASP动态数据采集系统和加速度传感器，实验采用手锤瞬态击振，采集桩的自由振动信号.

模型桩损伤识别的实验过程可分为4种工况，工况一：将模型桩简支，测得桩的振动频率，然后根据频率进行模型桩物理参数修正，继而进行基桩简支情况下的损伤识别；工况二：将模型桩固结在地面上，测得桩的振动频率；工况三：将模型桩放进预先挖好的基坑中，测得无桩周土情况下基桩的振动频率；工况四：进行无桩周土情况下基桩的损伤识别，然后将模型桩周围回填均质砂土并捣实，测得基桩的振动频率，进行有桩周土情况下基桩的损伤识别.实验设备及桩的各种工况如图2所示.

模型桩采用长径比为10的预制混凝土模型

图2 实验设备及各个工况下桩的示意图Fig.2 The pictures of equip ment and all conditions

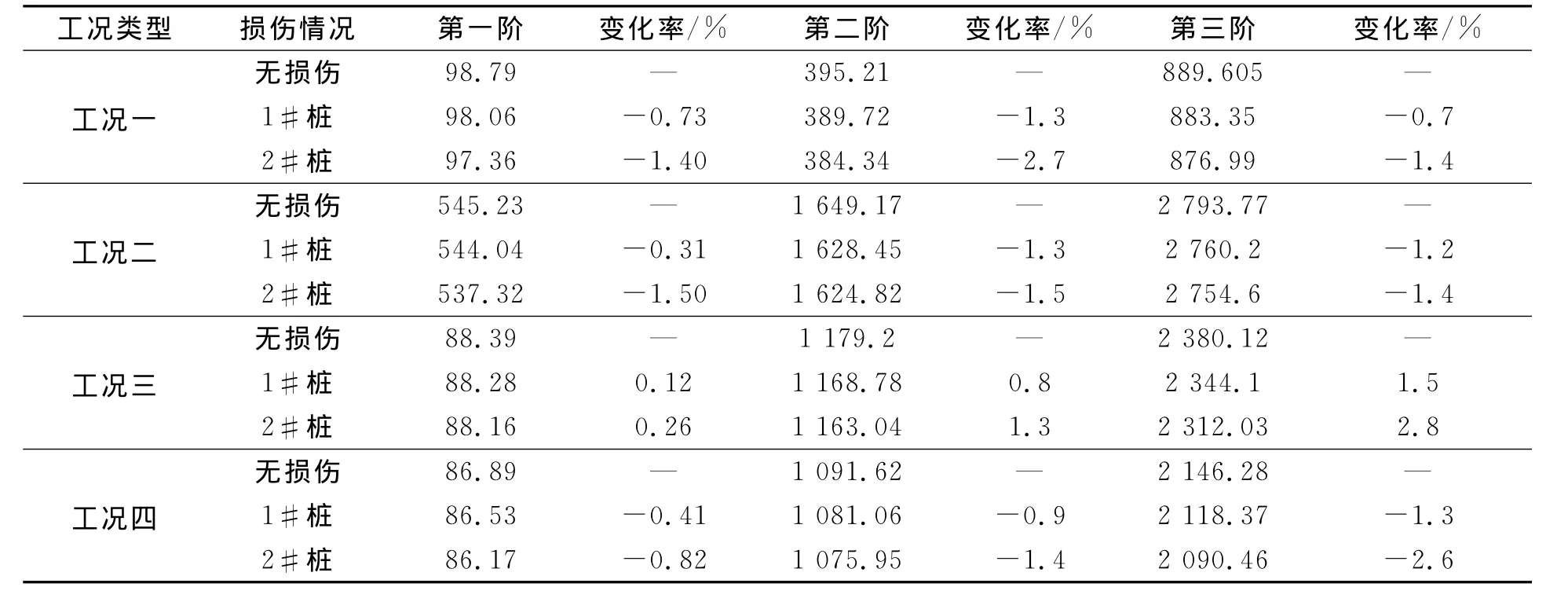
表2 桩各种工况的频率值Tab.2 The frequency value of every pile condition Hz

模型桩划分为10个单元，每个单元长0.15 m.分别对四根桩进行损伤处理，按照实验工况中的方法进行处理，将横截面面积损伤量换算成刚度损伤量，即工况二为单元3损伤24.2%，工况三为单元3损伤34.4%，工况四为单元3和8损伤24.2%，继而进行模态实验，实验测得各种情况下桩的频率值如表2所示.将表3中的数据代入损伤识别程序中，对4种工况分别进行损伤识别，得到损伤识别结果的柱状图如图3所示.

图3 各工况下损伤识别结果Fig.3 Identification result in all case

从图3中可以看出用摄动理论进行缺陷定量分析，不论是一处缺陷或多处缺陷、也不论缺陷在什么位置，识别出的结果均与设定的缺陷值基本吻合，4种工况识别出的结果误差最大的是工况一的1＃桩，误差为3.7%，其余的误差均在1%左右，这种识别结果能够满足工程需要.

4 结论

（1）建立了考虑桩周土体对桩身振动的弹性作用和阻尼作用的桩土体系的力学模型；

（2）基于基桩振动理论与矩阵摄动理论推出了基桩缺陷定量识别的公式及其求解方法；

（3）通过5根混凝土模型桩的试验，对所提出的基桩缺陷识别方法进行了验证；

（4）该方法使用基桩的固有频率这一绝对量识别基桩缺陷，还可以识别基桩的缓变型缺陷和混凝土的整体老化问题，弥补了目前低应变方法的不足.

［1］ AWREJCEWICZ J，PYRYEV Y.Dynamic damper of vibrations with ther moelastic contact［J］.Archive of Applied Mechanics，2007，77（5）：281－291.

［2］ WANG T，WANG K H，XIE K H.An analytical solution to longitudinal vibration of a variable modulus pile of infinite segments［J］.Acta Mechanica Solida Sinica，2001，14（1）：67－73.

［3］ 王靖涛.桩基完整性动力检测的定量分析［J］.施工技术.1994，21（2）：18－20.

［4］ HAN Y C.Dynamic vertical response of piles in nonlinear soil［J］.Jour nal of Geotechnical and Geoenvironmental Engineering，1997，123（8）：710－716.

［5］ 徐斌，高跃飞，余龙.MATLAB有限元结构动力学分析与工程应用［M］.北京：清华大学出版社，2009：106－110.

［6］ 李东旭.高等结构动力学［M］.北京：科学出版社，2010.

［7］ 杜思义，唐军，陈淮.基于摄动理论识别悬臂梁损伤方法的试验研究［J］.世界地震工程，2009，25（4）：64－69.

［8］ 杜思义.基于频率变化与单元矩阵摄动理论的结构损伤识别方法研究［D］.重庆：重庆大学资源与环境工程学院，2005：43－72.

［9］ EI NAGGAR，M，NOVAK M.Nonlinear axial interaction in pile dynamics［J］.Jour nal of Geotechnical Engineering，1994，120（4）：678－696.

［10］NOVAK M，NOGAMI T，ABOUL E.Dynamic soil reaction for plain strain case［J］.Jour nal of the Engineering Mechanics Division，1978，104（4）：953－959.