半封闭圆柱形衬砌结构振动响应的解析解

陈学丽，闻敏杰，张 斌

（1.嘉兴职业技术学院 生物与环境分院，浙江 嘉兴314036；2.上海市电力公司，上海200072）

0 引言

衬砌结构动力响应分析可用于地铁隧道、海底隧道、石油运输管道等工程领域.近年来，该问题一直是国内外研究的热点.T.Senj untichai和R.Rajapakes［1］研究了饱和土中圆柱形孔洞的动力响应，借助Laplace变换和势函数，得到了隧洞边界透水条件下位移、应力和孔压解答.杨峻等［2］利用积分变换法推导了饱和土中圆形孔洞动力响应的解析.徐长节等［3］求得了具有球形空腔饱和土动力响应的解析解，并分析了边界排水或不排水条件下位移、应力和孔压随时间的变化规律.上述都考虑了土体中液固耦合作用，但都忽略了衬砌的影响.

为此，U.Zakout和N.Akkas［4］采用加权残值法研究了弹性土和壳体衬砌耦合动力响应，并给出了瞬时、平移和最小叶等响应模式条件下的解析结果.S.E.Kattis等［5］在 Mei和Foda基础上［6］，研究了具有任意形状的平面隧洞饱和土动力响应的数值解，并与有限单元法进行了比较.高盟等［7］研究了均布Heaviside荷载作用下饱和土中圆柱形弹性衬砌结构的振动响应.蔡元强等［8］研究了爆炸荷载作用下饱和土中具有壳体衬砌结构的圆形隧道振动响应.上述研究虽考虑了土体和衬的相互作用，但未研究隧道的渗透性对响应幅值的影响.此后，X.Li［9］基于实际工程中隧道模型，建立了隧道部分透水的条件，刘干斌等［10］在此基础上对黏弹性饱和土中隧道动力响应进行研究.而上述都未考虑衬砌的黏性.

作者考虑土骨架和衬砌结构的黏性，求解了轴对称荷载和流体压力作用下饱和黏弹性地基中半封闭衬砌结构的动力响应.

1 饱和土中衬砌结构动力响应

无限饱和土中有一衬砌内外半径分别为R1和R2，厚度为d＝R2－R1的无限长深埋圆形隧道，衬砌内分别受到圆频率为ω的轴对称荷载和流体压力为虚数单位，如图1所示。不计体力时，由几何和物性特征可知，该问题视为轴对称平面应变问题分析.将衬砌视为均匀黏弹性介质，借助Kel vin－Voigt本构模型，在极坐标下以位移表示的动力方程为：

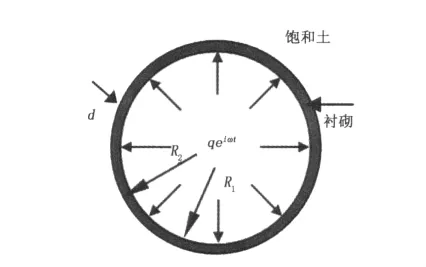
图1 计算模型Fig.1 Analytic model

式中：λL，GL为材料常数衬砌的黏滞阻尼系数，量纲为s分别为黏性材料膨胀和剪切系数；为径向位移；ρL为材料密度.

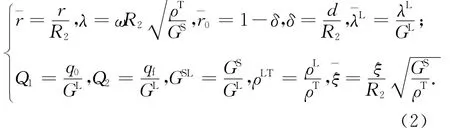
式中：GS为土体剪切波速；ρT＝（1－n）ρs＋nρf为土体总密度；n为孔隙率；ρs，ρf分别为土骨架和孔隙流体的密度.

于是，利用式（2）、式（1）可简化为

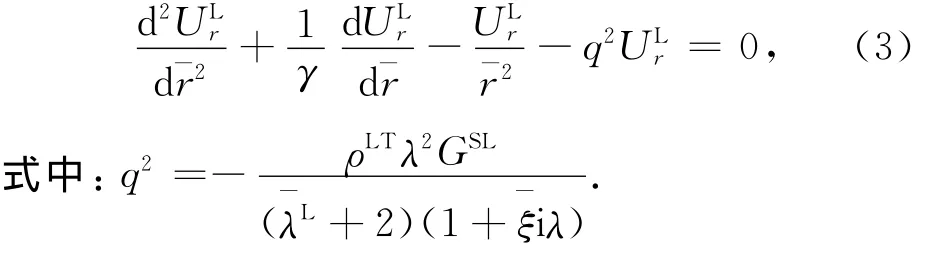
式（3）易解得

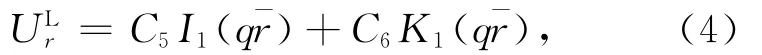
其中，C5，C6为待定系数；I1（x），K1（x）分别为1阶第一和第二类变形Bessel函数.

利用位移和应力的关系，可得衬砌的径向应力为

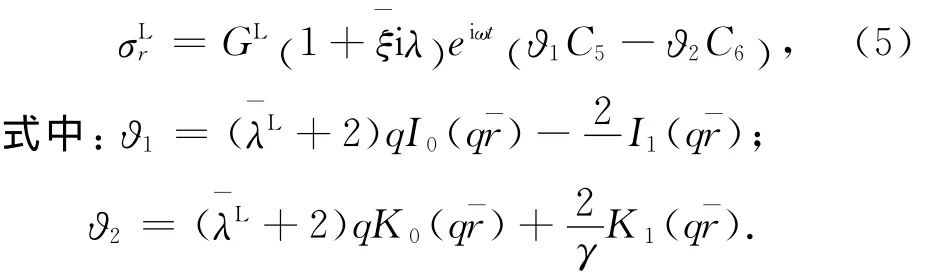
2 饱和土的动力响应

不计体力，在轴对称平面应变条件下，饱和土在动力荷载下的运动方程为［11］

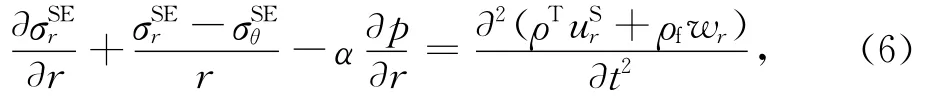
其中，σSEr，σSEθ分别为土骨架的有效径向和环向应力；p为孔隙水压力；uSr为径向位移；wr为流体相对于土骨架的径向位移.

利用Kelvin－Voigt本构模型描述土骨架的应力—应变本构关系［12］

式中：λS，GS为土骨架的Lame常数；分别为土体和流体相对于土体的体应变；为材料膨胀系数；α，M分别为表征土颗粒和孔隙流体压缩性的常数.

孔隙流体运动方程为

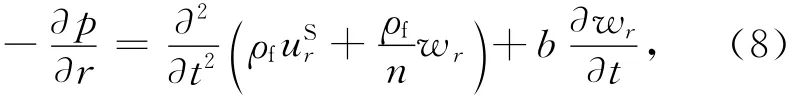
式中：b＝η0／ks为流固相互作用系数；η0，ks分别为流体绝对黏度和渗透系数.

引入如下位移势函数

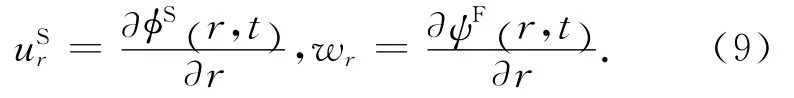
由式（6）～式（9），可得用势表示的动力方程为

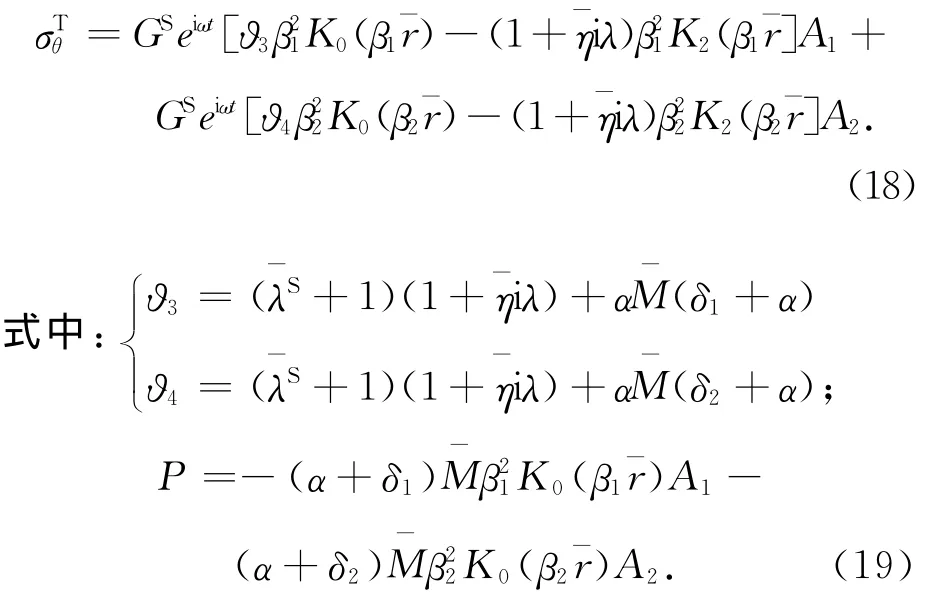
3 边界条件

X.Li认为实际工程中绝大部分隧道边界处于透水与不透水之间，即半封闭状态.为此，借助于达西定律建立了部分透水边界条件［9］.

首先，考虑轴对称荷载 （q0eiωt）作用，假设衬砌和土体完全接触.根据饱和土与衬砌结构界面处位移和应力连续，可得

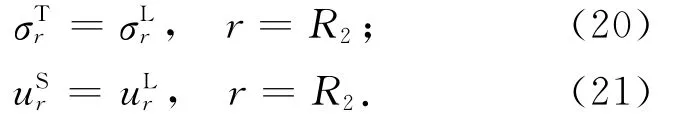
在衬砌结构的内边界上（r＝R），外荷载等于衬砌的径向应力

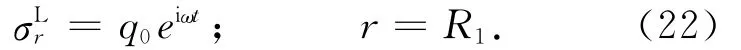
设衬砌外边界的水头为P2，内边界的水头为P1.在外荷载作用下，P2＝p，P1＝0.由此，根据达西定律，可知衬砌中的流体流量为［9］

土体中的流体流量为

式中：γw为流体重度；vs，vl分别为土体和衬砌中的流体流量；kl为衬砌的渗透系数；k＝为衬砌和土体的相对渗透系数.

由此，利用式（4）～（5）和式（16）～（19）代入边界条件式（20）～（25），可求得待定系数A1，A2，C5，C6的具体表达式.因此，可得轴对称荷载作用下半封闭衬砌结构动力响应解析解.

再次，考虑流体压力 （qfeiωt）作用，衬砌外边界上 （r ＝ R2）的位移和应力条件同式（20）和（21）.在衬砌结构的内边界上 （r ＝ R1） ，设流体压力全部由孔隙水压力承担，则

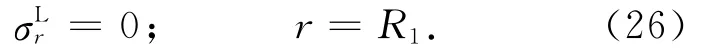
在流体压力作用下，P2＝p，P1＝qfeiωt.利用式（23）和（24），则部分透水边界条件为

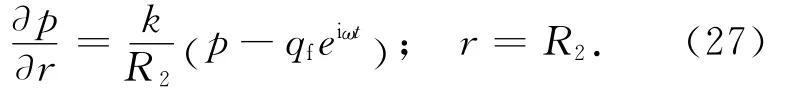
由此，利用式（4）～（5）和式（16）～（19）代入边界条件式（22）～（25）和式（26）、（27），可求得待定系数A1，A2，C5，C6的具体表达式.因此，可得流体压力作用下半封闭衬砌结构的动力响应解析解.

4 与已有解析结果对比分析

首先，将作者结果与一般单相黏弹性土中衬砌结构的动力响应进行对比.当饱和黏弹性土体中流体密度ρf＝0时，土体中不含流体，退化为一般理想的黏弹性介质.取如下参数：

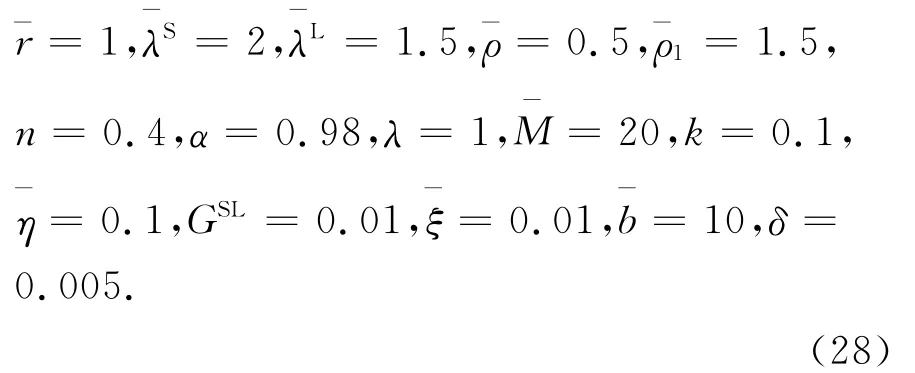
其余参数按式（28）取值，图2表示不同衬砌厚度时分别给出了单相与饱和黏弹性土时衬砌响应幅值的对比.图2（a）反映轴对称荷载作用下衬砌径向位移幅值随无量纲频率的变化.在稳态振动时，饱和黏弹性土中衬砌无量纲位移幅值的峰值明显大于单相土时位移幅值的峰值，但随着频率的增加衰减较单相土时要快.同时，产生的共振效应也越明显，但基频略小于单相土时共振效应的基频.图2（b）反映轴对称荷载作用下衬砌径向应力幅值随频率的变化曲线.可见，当频率小于1时，两种土体时的衬砌结构动力响应差异较小，而随着频率增加，特别是无量纲频率在1～3时，饱和土时衬砌的应力幅值大于单相土时的应力幅值，当频率再增大时，两者结果几乎相同.

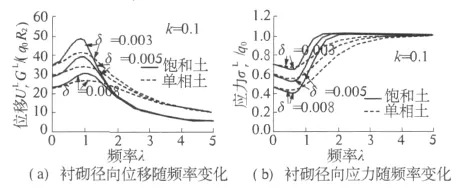
图2 单相黏弹性土与饱和黏弹性土对比（轴对称荷载）Fig.2 Comparison of single viscoelastic soil and satur ated viscoelastic soil

再次，将本文结果与文献［10］进行对比，该文献假设衬砌为柔性，即弹性模量为零.又认为衬砌厚度相对于隧洞半径很小，不区分荷载是作用在衬砌内边界上还是外边界上，即忽略了衬砌的厚度.为了与该文比较，令衬砌的剪切模量GL＝0，并采用文献［10］的边界条件.其余参数取值同式（28）.图3分别给出了本文和刘干斌等［10］两种解的土体径向位移和孔隙水压力随频率变化.由图3（a）可见，轴对称荷载作用下柔性衬砌时的土体径向位移幅值的峰值明显大于弹性衬砌条件下的位移幅值的峰值，基频也要略大于刘干斌解的基频.而孔压也有较明显差异，作者在低频时的孔隙水压力小于刘干斌等的孔压幅值.随着频率增加，两者差异不明显（图3（b））.

图3 本文解与刘干斌解对比（轴对称荷载）Fig.3 Comparison of solutions for this paper and Liu ganbin

最后，由于Ziekiewicz［13］提出了在低频振动时，忽略孔隙水的惯性效应不会影响问题的精度，而高频振动时会存在明显差异.为了验证该结果，作者取流体惯性项为零，即ρfω2＝0.

取渗透系数k→0或k→∞，其余参考式（28）取值，图4（a）和图4（b）分别给出了高频λ＝10和低频λ＝0.1时土体径向位移随无量纲半径的消散过程.可见，当系统为高频振动时，无论衬砌与土体界面处透水还是不透水，忽略水的惯性效应与考虑水的惯性效应都存在较大差异.而当系统为低频振动时，两种情况几乎完全相同，在图中无法显示.可见，该结果与Ziekiewicz的结果一致.

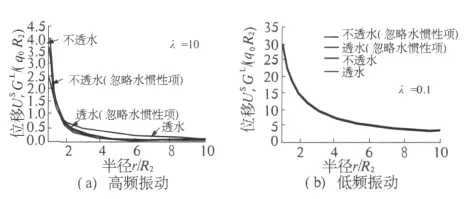
图4 土体径向位移随半径的消散（轴对称荷载）Fig.4 Radial displacement amplitude of soil dissipate with the radius increasing

5 数值结果与分析

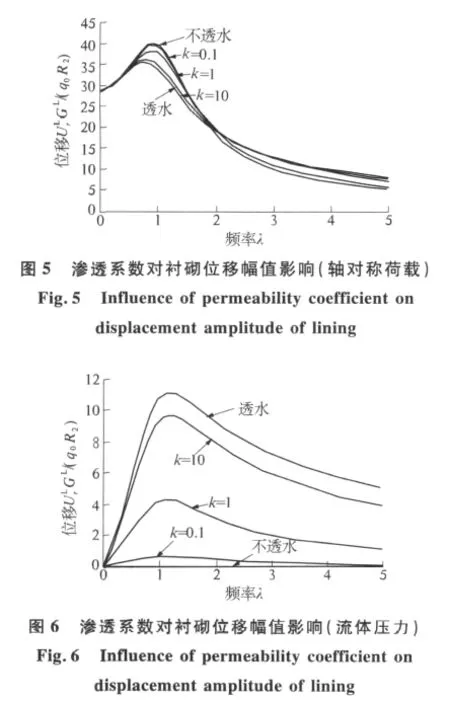
首先，考察k对衬砌径向位移幅值和径向应力幅值的影响.参数取值见式（28），图5～6反映分别在轴对称荷载和流体压力作用时渗透系数对衬砌的径向位移幅值的影响.图5中可见，随着k的增加，衬砌的位移幅值逐渐减小.当k＝0.1和不透水（k→0）时，衬砌的位移幅值很接近；当k＝10和透水（k→∞）时两者的衬砌位移幅值差异较小.这说明渗透系数k＝0.1和k＝10时衬砌和土体界面处已将分别处于不透水和透水状态.随着渗透系数的增加，响应幅值明显增大，透水情形下的响应幅值明显大于不透水情形下的响应幅值.不透水时衬砌响应幅值接近为零（图6）.

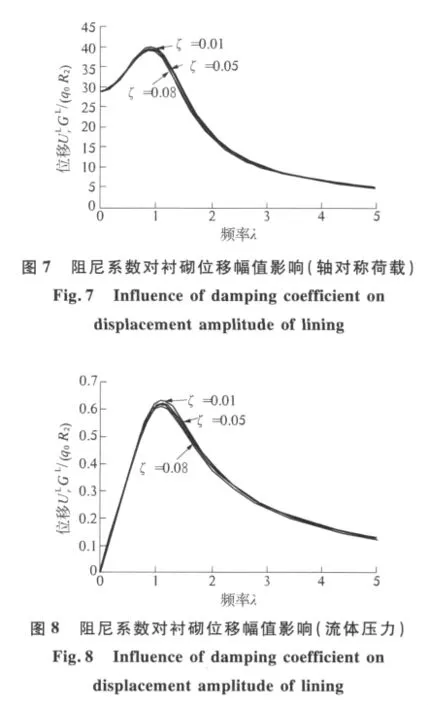
其次，讨论阻尼系数 对衬砌的径向位移幅值的影响.图7～8分别给出了轴对称荷载和流体压力作用时阻尼系数变化对衬砌径向位移幅值的影响.可见，不管是荷载作用还是流体压力作用，衬砌的阻尼系数对响应幅值影响较弱.随着阻尼系数的增加，响应幅值略有减小，但在低频时阻尼系数对响应幅值几乎无任何影响.

6 结论

作者推导了轴对称荷载和流体压力作用下饱和黏弹性地基中半封闭衬砌结构的动力响应.并分析了饱和土和衬砌各参数对动力响应的影响，得到如下结论：

（1）轴对称荷载作用下柔性衬砌时的土体位移幅值明显大于弹性衬砌条件下的位移幅值，基频也要略大于刘干斌解的基频，而在低频时的孔隙水压力小于刘干斌等的孔压幅值.

（2）轴对称荷载作用时，相对渗透系数对衬砌的径向位移幅值的影响较流体压力作用时的响应幅值明显要小.随着渗透系数的增加，轴对称荷载作用时响应幅值逐渐减小，而流体压力作用时响应幅值明显增大.

（3）衬砌的黏滞阻尼系数对衬砌的径向位移幅值影响较小，随着阻尼系数的增加，响应幅值略有减小.

［1］ SENJUNTICHAI T，RAJAPAKSE R.Transient response of a circular cavity in a poroelastic mediu m［J］.International Journal for Nu merical and Analytical Methods in Geo mechanics，1993，17（6）：357－383.

［2］ 杨峻，宫全美，吴世明，等.饱和土体中圆柱形孔洞的动力分析［J］.上海力学，1996，17（1）：37－45.

［3］ 徐长节，蔡袁强，吴世明.饱和土中球空腔的瞬态动力响应［J］.力学学报，2000，32（4）：473－480.

［4］ ZAKOUT U，AKKAS N.Transient response of a cylindrical cavity with and without a bonded shell in an infinite elastic medium［J］.International Journal of Engineering Science，1997，35（12／13）：1203－1220.

［5］ KATTIS S E，BESKOS D E，CHENG A H D.2D dynamic response of unlined and lined tunnels in poroelastic soil to har monic body waves［J］.Earthquake Engineering and Str uctural Dynamics，2003，32（1）：97－110.

［6］ MEI C C，SI B I，CAI D.Scattering of simple harmonic waves by a circular cavity in a fluid－infiltrated por o－elastic mediu m［J］.Wave Motion，1984，6：265－278.

［7］ 高盟，高广运，李大勇.考虑耦合质量影响的均布突加荷载作用下衬砌结构的瞬态响应［J］.岩土工程学报，2011，33（6）：862－868.

［8］ 蔡袁强，陈成振，孙宏磊.爆炸荷载作用下饱和土中隧道的瞬态动力响应［J］.岩土工程学报，2011，33（3）：361－367.

［9］ LI X.Stress and displacement fields around a deep circular tunnel with partial sealing［J］.Co mputers and Geotechnics，1999，24（2）：125－140.

［10］刘干斌，顿志林，谢康和，等.粘弹性饱和土体中半封闭圆形隧洞的稳态问题分析［J］.中国铁道科学，2004，25（5）：78－83.

［11］BIOT MA.Theor y of pr opagation of elastic waves in a fluid－saturated porous solid［J］.The Journal of the Acoustical Society of America，1956，28（2）：168－178.

［12］ERINGEN A C.Mechanics of co mtinua［M］.New York：Huntington press，1980：385－406.

［13］ZIEKIEWICZ O C，SHIOMI T.Dynamic response of saturated porous media：the generalized Biot formulation and its nu merical solution［J］.Inter national Jour nal for Nu merical and Analytical Methods in Geomechanics，1984，8：71－96.