超级拥挤公交网络均衡配流

黄正锋 王景辉

（东南大学交通学院1） 南京 210096） （同济大学交通运输工程学院2） 上海 201804）

0 引 言

公交乘客均衡配流问题是公交规划与管理的重要基础．为了使公交配流结果能够反映公交载运工具拥挤现状，众多学者在文献［1－5］中提出了各种求解拥挤影响下的公交均衡配流模型，这些模型在公交路段阻抗函数的表示方面存在不同．虽然文献［6］考虑了公交能力约束，并建立了随机公交配流模型，模型中公交路段能力约束条件所对应的拉氏乘子代表乘客的拥挤延误时间，但是模型假定乘客的等车费用和车辆运行费用皆为定值，不能反映拥挤带来的费用变化情况．综合考虑以上公交均衡配流模型的优缺点之后，笔者建立的模型假定公交出行费用受拥挤影响，是一个与流量相关的增函数，同时考虑车辆运行路段的流量受车辆运营能力的限制．提出的模型求解算法尤其适用于高峰时期乘客流量大于线路运营能力的超级拥挤公交网络均衡配流．

1 公交网络表述

一般的公交网络是由一系列公交车站和公交线路等组成，一个具有4个公交站点、4条公交线路的公交网络如图1所示，其中节点N1，N2，N3，N4代表上下车以及换乘的公交站点，公交线路L1，L2，L3，L4经过不同站点．

图1 一般公交网络

为了便于将公交网络分成路段描述，将上述用公交线路表示的公交网络进行扩展，扩展后的公交网络由一系列节点和连接节点的路段组成，节点仍代表车站，路段分成公交运行路段、等车路段、下车路段（包括换乘功能）．由3种路段表示的对图2进行扩展后的公交网络见图2，其中点线代表等车路段，实线代表车辆运行路段，点划线代表下车路段．

图2 公交扩展网络

2 公交路段费用函数

等车路段为a，fa表示通过a的公交线路发车频率，在非拥挤状态下，假定车辆到达间隔时间服从均值为1／fa指数分布，乘客到达车站数量服从均一分布，则站点乘客的平均等车时间为1／fa．而随着需求量的增加，车站的排队就会增长，导致乘客在车站的平均等车时间连续增加．假定除了车辆发车间隔之外，站点等车人数（va）和车内剩余人数（vd）都会影响乘客的等车费用．于是，等车路段a的费用函数可表示为

式中：α1，β1和ρ为正的参数；ub为紧接路段a的车辆运行路段b的公交线路运营能力．设vb为路段b的客流，根据流量守恒公式vb＝va＋vd，式（1）可变形为

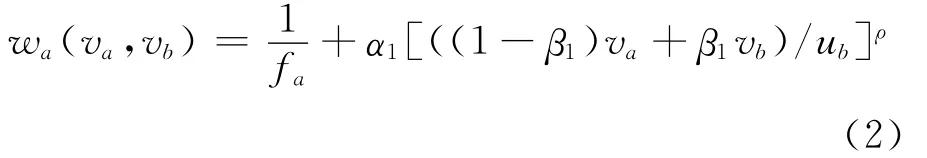
式中：参数β1的取值范围在0和1之间．

车辆运行路段b的费用包括两部分，即与流量无关的车辆运行时间费用tb（对于城市道路网络中运行的公交车辆，假设私家车辆对其速度没有影响）和由车内拥挤造成的不舒适度费用，则车辆运行路段b的费用函数形式可表示为

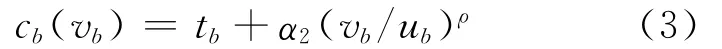
式中：α2为正的参数．

3 公交均衡配流模型

假设W 为公交网络OD对的集合，在一个拥挤程度不是很大的公交网络中，对于任意一个OD对w∈W，如果公交路段流量满足方程

一般认为此公交网络路段流量可行．方程（4）为路径流量和OD需求之间的守恒关系，其中：Rw为OD对w之间的可行路径集，hr为路径r∈Rw上的公交流量；gw为OD对w之间的公交需求量．方程（5）为路径流量和路段流量之间的关联等式．式中：R为可行路径集；A为公交路段集；δar为路段a与路径r之间的关联矩阵元素，a在r上时取1，否则取0．方程（6）为公交车辆运行路段能力约束，B为公交车辆运行路段集合．

如果公交网络客流处于非常拥挤的状态，则在式（4）守恒的前提下式（6）很难得以满足．为了使公交配流结果满足线路运营能力约束，必需从过多的总需求中剔除剩余OD量．将OD对w中由于公交路段流量已饱和而产生的剩余OD量记为dw．dw的取值必需满足以下2个条件：（1）若OD需求gw未造成公交路段能力约束的破坏，则dw＝0；（2）若OD需求gw在公交网络上的配流结果破坏了公交路段能力约束，则dw≥0，以使式（6）继续得以满足．

为了满足上述两个条件，采纳文献［7］所建立超量需求网络的思想，在OD对间增设一条虚拟路段．路段阻抗取为无限大的一个定值M，不随客流大小而改变，也不受能力限制．进行路网均衡配流时，当流量未接近运营能力时，OD间真实公交路径的出行费用不超过M；而随着流量渐渐接近运营能力，式（4）将抑制流量继续增大的趋势（具体求解时，可以通过加入惩罚项保证约束条件的成立）．此时，增设路段呈现两点性质：（1）当网络中还有其他路径可供选择时，增设路段上的流量为0；（2）当其他路径都已达到饱和的状态时，剩余OD量将转入增设路段．

对比增设路段流量和剩余OD量发现，增设路段上的客流变量满足dw取值的要求．因此可在所有OD对间增设一条费用都为M的公交路段，对公交网络进行变化．变化后的公交网络中，假设路段集为¯A，路径集为¯R．于是流量方程（4）、（5）变为

不管公交网络拥挤状况如何，可行的公交路段客流必定满足关系式（6）～（8）．用Ω表示公交路段流量可行解集合．如果Ω中有满足Wardrop均衡条件的解，且有运营能力约束的公交路段费用都已附加惩罚项，则其公交用户均衡配流模型可写成以下变分不等式形式

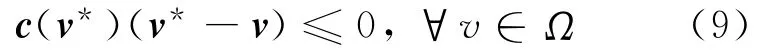
式中：c（·）为公交路段的费用向量；v为公交路段的客流向量；v＊为公交路段均衡解向量．由于公交网络中等车路段费用函数不具有对称的雅可比矩阵，因此上述形式无法建立相应的等价极值模型．

4 求解算法

即使费用函数不具有单调递增性，对角化算法的收敛性也很好［8］，论文采用对角化算法求解模型（9）．使用对角化算法求解问题的关键在于对子问题的处理，用¯c（v）表示对角化后的公交路段费用函数矩阵，则模型（9）产生的子问题形式表述如下

式（10）中包含有车辆运行路段上的客流能力约束，可以采用惩罚函数或拉氏乘子方法求解［9］．本文采用文献［10］设计的内罚函数求解方法，将式（10）转化为无容量约束的问题，由于该方法的子过程中仍保留F－W算法的形式，因此易于求解实施．

将内罚函数法应用于式（10）时，可将该问题的目标函数扩展为

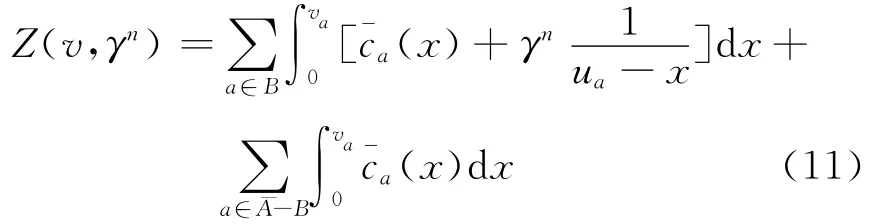
步骤0 预设γ0和σ（0＜σ＜1）值，将OD对w∈W 的增设路段流量设为gw，形成初始可行内点v0，n＝1．和不变的增设路段费用作为阻抗函数进行客流全有全无分配．此时产生一组路段流量ya，a∈¯A．

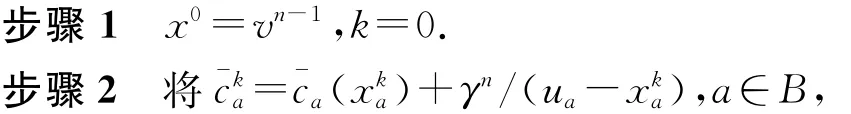
步骤3 寻找使Z（xk＋λ（y－xk），γn）最小化的步长λ＊，步长范围限定为0≤λ≤ min｛1，

步骤6 如果｜P（vn，γn）／Z（vn，γn）｜≤K2或者n＝MN2就停止；否则，γn＋1＝σγn，n：＝n＋1返回步骤1．

算法中，K1和K2是预先确定的收敛标准，MN1和MN2是最大允许迭代数，P（vn，γn）＝｛lg（ua－vna）－lg（ua）｝是扩展目标函数的若罚项与扩展目标函数值相比足够小的话，即判定算法收敛．由于问题P中各OD对间都增设了1条无容量限制的路段，因此开始将OD需求量全部分配在这些路段上，便能形成初始内点，不需要使用寻找初始内点的算法，加快了求解效率．

5 算 例

图3的扩展公交网络含有一个OD对 （N1，N4），首先在OD间增设1条无能力约束、费用无穷大的公交路段（此处费用取1 000 min）．与费用函数相关的系数取α1＝α2＝1，β1＝0．2，ρ＝2，下车路段费用取为0，其他参数及相应的计算结果见表1．OD需求分别取100和240人的配流结果如表中第4，5列所示．当需求为100人时，网络拥挤程度不是很大，此时剩余OD量为0，即所有乘客的公交出行需求都得到满足．当需求为240人时，公交网络呈现出超级拥挤的状态，从起点（N1）出发的两条线路L1，L2都被乘客挤满，流量趋于能力大小，而运算得到的剩余OD量为41，即有41个乘客因为拥堵未能在规定时段坐上公交车辆．

上述算例中，OD对（N1，N4）间存在5条实际路径和1条虚拟路径．公交实际路径用车辆运行路段表示分别为R1），R2），R3，，），R4（，），R5（L12，L13，L14）．图3显示需求为240的情形下均衡配流后公交实际路径出行费用．对角化算法最后一次迭代对P问题的解中，实际 路 径 的 惩 罚 费 用 分 别 是966．54，963．29，963．29，999．51，1 002．34 min．将实际路径的出行费用与惩罚费用相加即为含有惩罚项的路径总费用，对比后得出OD间最小总费用公交出行路径包含R1，R2，R3以及虚拟路径，因此乘客公交出行可选择的最小路径为R1，R2和R3．但是观察图3发现R1的实际出行费用比R2和R3小，说明求解算法已经考虑了R1的容量限制条件．

表1 参数及不同需求公交均衡配流结果

图3 需求240情形下公交路径出行费用

6 结束语

针对拥挤影响和能力限制双重约束下的公交用户均衡配流问题设计模型与算法．模型通过在OD间增设阻抗无穷大的路段，尤其能够解决超级拥挤公交网络状态下乘客需求过剩的公交均衡配流问题，以此保证公交线路的能力限制条件真正得以满足．算例证明了内罚函数法求解对角化后的子问题是可行的，只是求解过程较为复杂，如何提高求解效率仍需进一步研究．

［1］Spiess H，Florian M．Optimal strategies：a new assignment model for transit networks［J］．Transportation Research Part B，1989，23：83－102．

［2］De Cea J，Fernández E．Transit assignment for con－gested public transport systems：an equilibrium model［J］．Transportation Science，1993，27：133－147．

［3］Wu J H，Florian M，Marcotte P．Transit equilibrium assignment：a model and solution algorithms［J］．Transportation Science，1994，28：193－203．

［4］四兵锋，高自友．城市公交网络均衡配流模型及算法研究［J］．公路交通科技，1998，15（1）：41－44．

［5］宋一凡，高自友．拥挤条件下的公交平衡配流［J］．中国公路学报，1999（12）：88－95．

［6］Lam W H K，Gao Z Y，Chan K S，et al．A stochastic user equilibrium assignment model for congested transit networks［J］．Transportation Research Part B，1999，33：351－368．

［7］Gartner G H．Optimal traffic assignment with elastic demands：a review（part II）［J］．Transportation Science，1980，14：174－191．

［8］Florian M，Spiess H．The convergence of diagonalization algorithm for asymmetric network equilibrium problem［J］．Transportation Research Part B，1983，18：477－483．

［9］Patriksson M．The traffic assignment problem：models and methods［M］．Utrecht：VSP，1994．

［10］Inouye H．Traffic equilibrium and its solution in congested road networks［C］∥Proceedings of IFAC Conference on Control in Transportation Systems，1987：267－272．