自适应谱线增强器在生物雷达中的应用

陈铁军 付瑞玲

(郑州大学电气工程学院，河南 郑州 450001)

0 引言

生物雷达是地震、灾害救援的专用设备，它不仅能从携带有微弱人体生命体征(呼吸、体动等)的雷达回波信号中检测出人体的生命参数，而且还可以穿透一定的介质(砖墙或废墟)，并间隔一定的距离探测人体的生命体征，发现存活、被困人员，使受困人员得到及时营救［1－3］。然而，雷达在接收生命信号的同时不可避免地会采集到诸如背景噪声、地杂回波甚至灾害源等信号，这些信号容易与选择的生命信号产生交叠。因此，对采集信号处理的效果直接决定了生命探测仪性能的优劣。

为解决这一问题，基于变步长自适应算法的各种信号处理的方法不断涌现［4－7］。传统的变步长自适应算法均需要预先给定参考信号。但在救援环境复杂以及废墟下存活人体的个体差异，在生物雷达信号处理中很难找到一个理想的信号作为参考信号。为解决这一问题，本文提出了基于误差变化率的变步长最小均方误差(least mean square，LMS)自适应谱线增强算法。该算法不需要预先给定参考信号，而是以输入信号本身的延迟作为参考信号［8－14］。

1 自适应谱线增强器原理

自适应谱线增强器最早是由Widrow等人于1975年提出的。目前，基于自适应线性组合器的自适应谱线增强器已广泛应用于频谱估算、谱线估计以及窄带检测等领域。在窄带信号加上宽带信号的情况下，自适应谱线增强方法无需独立的参考信号就能将信号分离出来，从而提高了生命探测系统对微弱信号的检测能力，其原理如图1所示。

图1 自适应谱线增强器原理图Fig.1 The principle of adaptive spectral enhancer

如果在输入端加入的信号x(n)是1个窄带信号sN(n)和1个宽带噪声sB(n)的混合，由于窄带信号的自相关函数比宽带噪声自相关函数的时间相关半径要短。因此，当延迟时间Δ小于宽带噪声的时间相关半径而大于窄带信号的时间相关半径时，宽带噪声sB(n)将与sB(n－Δ)不相关，而窄带信号sN(n)与sN(n－Δ)仍然相关，因而自适应滤波器的输出将是窄带信号sN(n)的最佳估计。sN(n)+sB(n)与sN(n)相减后得到的是sB(n)的最佳估计，从而能将窄带信号sN(n)与宽带噪声sB(n)分离开来。这样，自适应滤波器的输出y(n)就是所需要的有用信号。

固定步长的LMS算法迭代公式为:

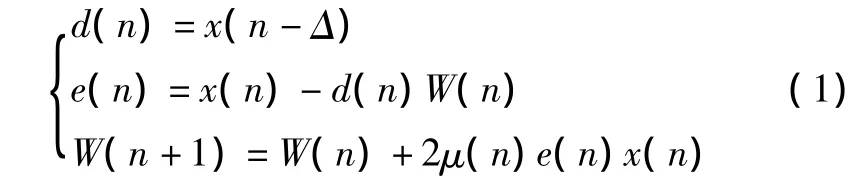
式中:x(n)为输入信号;d(n)为x(n)的延迟，作为参考信号;e(n)为误差信号;W(n)为权重系数;μ(n)为步长。

2 改进的谱线增强算法

初始收敛速度、时变系统跟踪能力以及稳态失调是衡量自适应滤波算法优劣的三个最重要的技术指标。在LMS算法中，最简单的学习速率参数选择是取μ(n)为常数，即:

式中:λmax为输入信号自相关矩阵的最大特征值。

这种方法会引起收敛与稳定性能的矛盾，即大的学习速率能够提高滤波器的收敛速率，但稳态性能就会随之降低;反之，为了提高稳态性能而采用小的学习速率时，跟踪速度和收敛就会变慢。因此，学习速率的选择应该兼顾稳态性能与收敛速率。一种简单而有效的方法就是在不同的迭代过程中使用不同的学习速率参数，即采用时变的学习速率。

文献［8］～［11］给出了几种变步长自适应算法，基本解决了固定步长存在的矛盾。以上所有算法均需要理想信号作为参考信号，从而得到越来越小直至为0的误差信号来控制μ(n)的变化［8－11］。但是自适应谱线增强系统的理想误差并不趋于0，而是近似于宽带噪声，所以即便系统已经完全跟踪上时，步长因子μ(n)并不为0，仍将继续迭代。

本文提出了一种基于误差变化率的变步长自适应LMS谱线增强算法。该算法采用误差变化率来控制步长因子μ(n)的变化，以保证当系统达到稳态时停止迭代。步长更新公式如下:

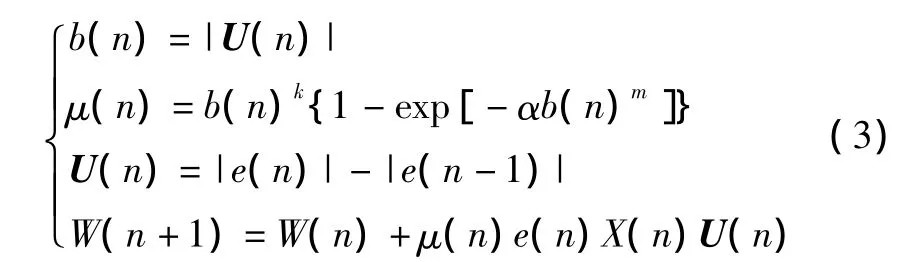
式中:k为步长控制因子;U(n)为步长向量;W(n)=［ω1(n)ω2(n)…ωM(n)］为滤波器的权系数，其中M为滤波器的阶数;α为控制函数形状的常数;m为调整因子;b(n)为误差变化量的绝对值。

3 算法收敛性能分析

步长μ(n)与各参数的关系曲线如图2所示。

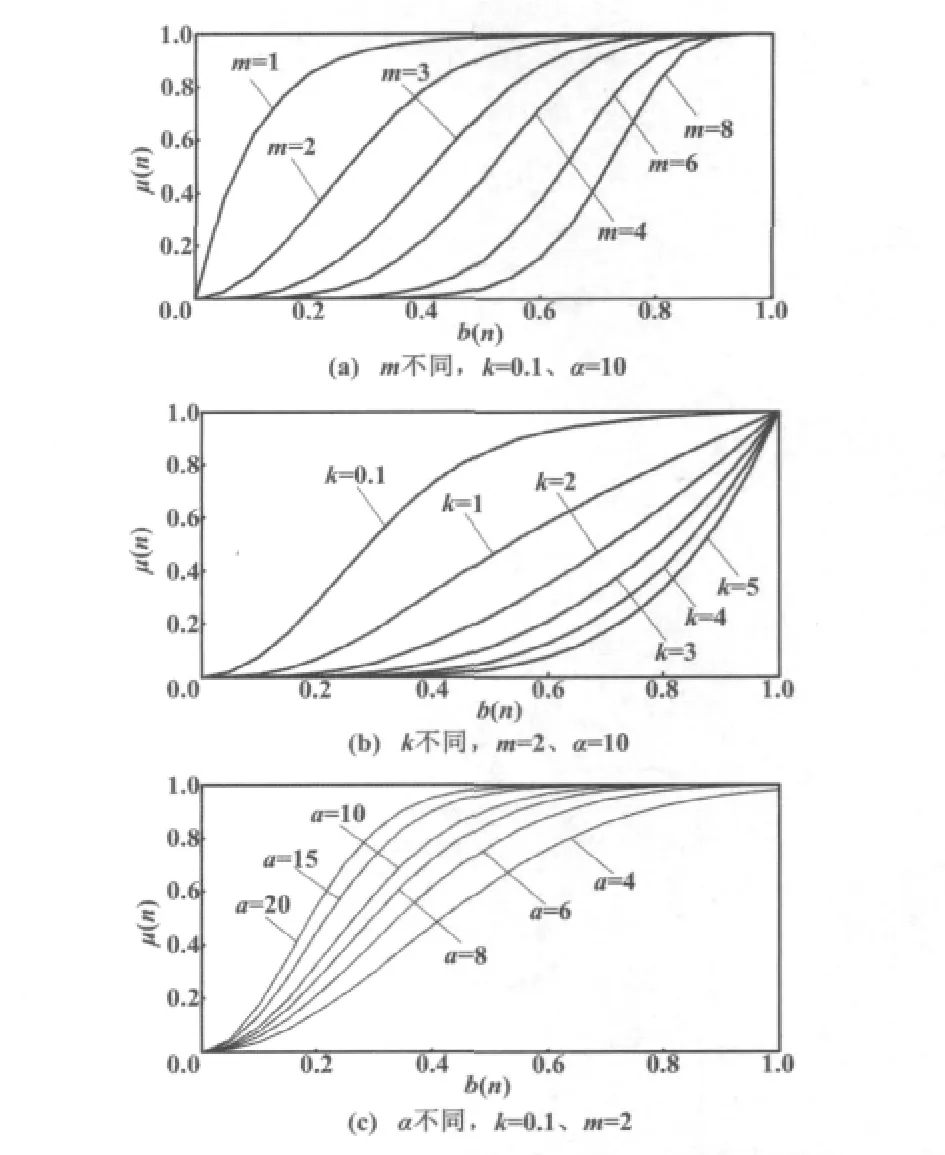
图2 步长μ(n)与各参数的关系曲线Fig.2 The relative curves between step size μ(n)and various parameters

从图2(a)可以看出，当m选择过小时，曲线比较尖锐，b(n)在接近0处变化时(算法已达到或将要达到稳态)，μ(n)变化太大，不具有缓慢变化的特性，易造成较大的稳态噪声;当m选择过大时，曲线底部形态比较平缓，会出现b(n)还未接近0处变化时μ(n)已成为0的情况，这样又可能造成较大的稳态噪声。从图2(b)可以看出，k从整体上影响算法的收敛速度。当k选择过大时，步长调整过早进入缓慢变化区域;当k选择过小时会增大稳态误差。从图2(c)可以看出，α控制函数的形状。当α选择过大时，误差变化率接近0仍有较大步长，稳态误差增大;当α选择过小时，步长较小且变化缓慢，收敛速度降低。因此，参数m、k和α应根据具体的系统环境与要求进行选择。

4 算法应用

因为生物雷达探测到的人的呼吸信号比较规律且接近正弦波［12］，所以本文采用正弦信号来模拟被探测人员的呼吸信号。通过对所采集数据的分析，杂波可以近似用高斯杂波表示。根据正常人的呼吸频率区间，设被探测人员的呼吸信号为被高斯白噪声污染的正弦信号。该信号的信噪比为5 dB、频率为0.4Hz的正弦信号。为了取得较小的稳态失调量和较短的收敛时间，各参数设置如下:α=600、k=2、m=4、Δ=20，同时，设置滤波器阶数为100。

文献［11］和本文算法提取的正弦信号波形如图3所示，两种算法的收敛曲线比较如图4所示。

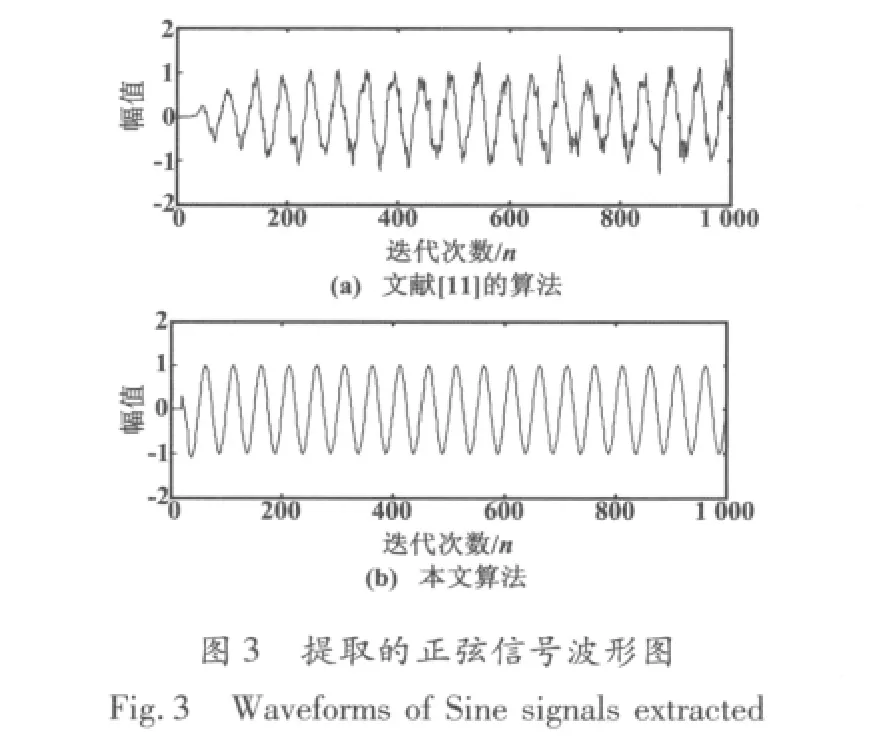
由图3、图4可知，本文算法具有良好的跟踪性能、较小的稳态误差以及良好的收敛性能。

5 结束语

本文分析了传统的LMS算法在生物雷达信号处理过程中的应用，根据固定步长算法以及文献中的变步长算法的不足，提出了一种新的变步长自适应LMS谱线增强算法。通过仿真试验可以看出，当系统发生突变时，该算法也能快速收敛，具有很好的鲁棒性，达到了很好的效果;在低信噪比的条件下，该算法也具有很好的跟踪性能。

［1］Linjc K，Wollschlaeger P.Microwave apexcardiography［J］.IEEE Transaction on Microwave Theory Technology，1979，27(6):618 －620.

［2］Misra D K.Scattering of electromagnetic waves by human body and its applications［D］.East Lansing:Michigan State University，1984:292－297.

［3］倪安胜.伤员探测中生命体识别技术研究［D］.西安:第四军医大学，2003:13－15.

［4］付玉峻，商文忠，张晗.一种自适应方向性技术在生命探测仪中的应用［J］.武警学院学报，2008(24):34 －35.

［5］张杨，王建琪，荆西京.基于自适应滤波的生物雷达干扰抑制方法［J］.仪器仪表学报，2009，30(4):807 －811.

［6］夏淑芳.自适应滤波技术在雷达式生命探测仪中的应用研究［J］.科技风，2009(13):260.

［7］张陆游，张永顺，潘克战.变步长自适应算法在雷达旁瓣对消系统中的应用［J］.空军工程大学学报:自然科学版，2008(4):25－28.

［8］Yasukawa H，Shimada S，Furukrawa I，et al.Acoustic echocanceller with high speech quality［C］//ICASSP，1987:2125 －2128.

［9］叶华，吴伯修.变步长自适应滤波算法的研究［J］.电子学报，1990，18(4):63 －69.

［10］罩景繁，欧阳景正.—种新的变步长自适应滤波算法［J］.数据采集与处理，1997，12(3):171 －194.

［11］高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29(7):1094 －1097.

［12］李杰，王健琪，荆西京，等.非接触生命参数检测系统动/静目标的识别技术［J］.第四军医大学学报:自然科学版，2005，26(20):1915－1918.

［13］黄春艳，张云鹏，黄红艳.基于灰色关联度的图像混合噪声的自适应滤波算法［J］.微电子学与计算机，2010，27(2):126 －128.

［14］毕国堂，王晓辉，周燕，等.基于粗集的图像混合噪声滤波算法［J］.计算机工程与设计，2009，30(21):4898－4900.