残差χ2检验法在联邦滤波中的应用

程洪炳 倪世宏 黄国荣 刘华伟

(空军工程大学工程学院，陕西 西安 710038)

0 引言

随着导航系统种类的增加以及系统结构的日益复杂化，导航传感器故障率已成为影响高性能动态系统完好性的一个重要因素［1－2］。建立在组合导航滤波器之上的系统级检测也因此成为保证系统输出数据完好性的关键［3］。

在联邦滤波器中，既可以基于子滤波器对每个传感器单独进行故障检测和隔离，也可以基于主滤波器进行整体性能检测［4－6］。灵活的结构特性使得基于联邦滤波器的故障检测技术受到了许多学者的关注［7］。然而，联邦滤波器结构的特殊性却使目前较为成熟的残差检验算法存在一定风险。针对这一问题，本文深入分析了残差χ2检验应用联邦滤波器时存在的问题，并提出了改进算法。

1 残差故障统计检验原理

基于残差的故障统计检测在导航系统故障检测算法中占有绝对优势。无论是观测量故障还是状态量故障，总会通过一定的奇偶关系反映在残差变化上。基于残差的故障统计检验原理就是通过检验残差的变化，检验并隔离故障。

带故障的离散系统模型如式(1)所示:

式中:X(k)为系统状态，且 X(k)∈Rn;Φ(k，k－1)为一步状态转移阵，且 Φ(k，k－1)∈Rn×n;Γ(k－1)为系统的噪声阵，且 Γ(k－1)∈Rn×r;H(k)为量测矩阵;w(k)、v(k)为相互独立的高斯白噪声序列，且w(k)∈Rr和 v(k)∈Rm;γf为随机故障向量;f( k，t)f为分段函数。

f(k，tf)的表达式如下:

式中:tf为传感器故障时刻。无故障时，f( k，tf)=0，卡尔曼滤波能够给出最小方差意义上的最优估计;反之，卡尔曼滤波变为次优，甚至失效。

基于残差的导航系统故障检测一般可描述如下。令r(k)为k时刻通过残差生成器(最小二乘法或卡尔曼滤波器)得到的残差序列，分布函数为F( k)，且有:

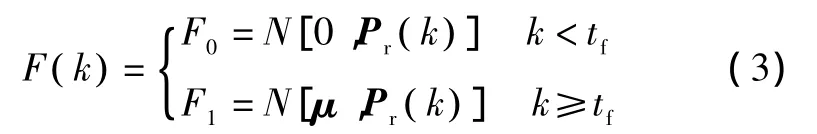
式中:μ描述了故障方向。故障检验算法就是要通过假设检验方法，检验残差r(k)的均值由0到μ的变化。根据μ是否已知，检测通常分为两类:①若μ已知，称为简单故障检测;②若μ未知，但已知μ∈Θ:{μTPr－1μ=b2}，称为复合故障检测。

导航系统故障检测通常被认为属于复合故障检测。因为对于一个多维残差序列，很难事先确定方向和幅度都已知的μ。但简单故障检测算法是复合故障检测算法的基础。

2 残差χ2检验算法描述

由于卡尔曼滤波器不受观测量维数的限制，又不要求量测矩阵H(k)必须列满秩。因此，多数导航系统内部均采用卡尔曼滤波生成残差［8］。预测残差序列又称新息序列，其表达式为:

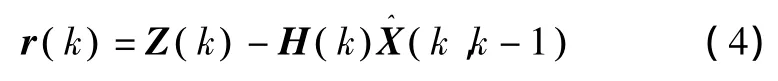
根据卡尔曼滤波方程，新息的协方差阵为:

残差χ2检验法实际上是一种基于预测残差序列的 χ2检验法，其中预报值 X^(k，k－1)为:

对r(k)作如下二元假设。

H0:无故障 E{ r(k)}=0，E r(k) rT(){ k}=Pr(k)

H1:有故障E{ r(k)}=μ，E{［r(k)－μ］［r(k)－μ］T}=Pr(k)

故障检测函数为:

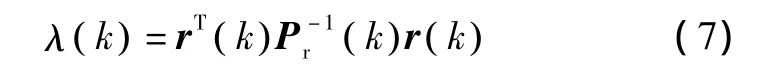
式中:m为量测矩阵Z(k)的维数。

故障判定准则为:

3 残差χ2检验问题分析

将残差χ2检验法应用于联邦滤波器传感器故障单独检验，局部估计预报值(k，k－1)一般通过以下两种方法计算。

①使用局部估计进行预测，即:

②使用全局融合估计进行预测，即:

式中:下标i和g分别表示局部滤波和全局滤波。

4 双“状态传播器”的改进

针对残差χ2检验法对软故障的不敏感性，提出了基于移动伪正常状态的残差χ2检验法和基于融合量测预报的故障检测方法［9－10］。这两种算法实际上都是基于“状态传播器”思想，能有效解决上述问题。为避免将一个已受污染的状态传播器作为参考系统，建议采用将双“状态传播器”思想引入残差χ2检验法，使用全局估计对其进行交替重置，具体算法如下。

考虑子滤波器残差为:

①状态传播器的重置

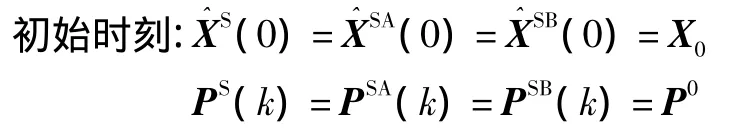
在系统正常工作状态下，两个状态传播器交替重置。设交替重置时间间隔为Δt，k0为重置时刻。(k)和PS(k)的计算过程如下。式中:上标S、SA、SB分别表示最终状态输出、状态传播器A输出、状态传播器B输出;Δt应该保证软故障能够积累到被检测的程度，假设设置合适，则能够保证重置时刻全局估计没有受到污染，那就可以很好地解决软故障跟踪问题。

如果系统在tf时刻被检测出故障，则精度会严重下降，因此，需要同时重置，即:

式中:j=k－Δt+1。

② 时间间隔Δt的选择。

Δt的选取原则是不能太小也不能太大。

5 仿真分析

考虑如下三维系统［11］:

设仿真时间为1000s，误检率为0.1，查 χ2分布函数表，可得门限TDi=6.251(自由度为3)。假设500～800s之间发生如下形式的软故障:Z1(k)=Z1( k －1)+0.05(k－500)。直接将残差χ2检验法应用于联邦卡尔曼滤波器的传统方法称为算法一，本文提出改进算法标为算法二，这两种算法的故障检测函数及漏检曲线如图1和图2所示。

图1 故障检测函数曲线Fig.1 The curves of fault detection function

从图1可以看出，在故障发生期间，改进算法的故障检测函数值比传统算法普遍要高，这在一定程度上克服了传统算法对软故障不敏感的缺陷。

图2 漏检曲线Fig.2 The curves of leak out of test

从图2可以看出，改进算法大约从548 s开始漏检情况很少发生，而传统算法漏检频发的状况一直持续到656 s左右。这从漏检风险的角度再次证明改进算法比传统算法对软故障检测的灵敏度更高。

以上两种算法的具体检测风险数据如表1所示。

表1 检测风险数据对比Tab.1 Inter-comparison of the detection risk

6 结束语

从上述研究可以看出，残差χ2检验法在联邦滤波器的系统级故障检测应用过程中，局部估计的次优性和自适应信息分配策略将对各子滤波器故障检测灵敏度产生影响。基于双“状态传播器”的改进算法能够有效改善局部估计次优性和自适应信息分配策略对故障检测灵敏度的不一致性，并且仿真结果也验证了该方法的有效性和正确性。

［1］Brumback B，Srinath M.A chi-square test for fault-detection in Kalman filters［J］.IEEE Transactions on Automatic Control，1987，32(6):552－554.

［2］Zhu Yanhua，Liu Jianye，Zeng Qinghua.Application of state chi—square test in damping Kalman filter of inertial attitude and heading reference system［J］.Chinese Journal of Scientific Instrument，2007，28(9):1569 －1576.

［3］Wong W E，Wei T T，Qi Y，et al.A crosstab-based statistical method for effective fault localization［C］∥20081stInternational Conference on Software Testing，Varification and Validation，2008:42 －51.

［4］Kehan G，Khoshgoftaar T M.A comprehensive empirical study of count models for software fault prediction［J］.IEEE Transactions on Reliability，2007，56(2):223 －236.

［5］Birsen Y.Statistical pattern analysis of partial discharge measurements for quality assessment of insulation systems in high-voltage electrical machinery［J］.IEEE Transactions on Industry Applications，2004，40(6):1579－1594.

［6］李金梁.基于联邦结构的多传感器自主式组合导航技术研究［D］.西安:空军工程大学，2007.

［7］Kerr T H，Brumback B D，Srinath M D.Comments on“a chi-square test for fault detection in Kalman Filters”［J］.IEEE Transactions on Automatic Control，1990，35(11):1277 －1278.

［8］秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998.

［9］王志胜.信息融合估计理论及其在航天器控制中的应用研究［D］.西安:西北工业大学，2002.

［10］邱恺.基于联邦结构的组合导航多传感器信息融合技术研究［D］.西安:空军工程大学，2005.

［11］王仲生，何红，陈钱.小波分析在发动机早期故障识别中的应用研究［J］.西北工业大学学报:自然科学版，2006，24(1):68 －71.