基于减容增效的超低比转速轴流式叶片水力设计
刘有余 韩 江
1. 安徽工程大学,芜湖,241000 2.合肥工业大学,合肥,230009
0 引言
轴流定桨式水轮机的特性曲线陡且窄,这决定了其对流量变化极为敏感。大多数此类水电站水资源季节分配不均,枯水期流量大为减小,很可能使水轮机的运行工况点远离有效工作区,导致出力急剧下降乃至带不上负荷,被迫停机弃水,这是一个困扰很多水电站的难题[1]。对很多轴流定桨式水电站而言,如能保留原有埋入过流部件不变,仅通过更换一个转轮,使之在原本不能发电的小流量工况下也能正常发电,将提高电站设备和水资源的利用率,大幅提高经济效益。
当前,国内外对轴流式转轮的研究大多集中于提高单机容量、效率和汽蚀性能等方面[2-3],很少有人致力于对现有机组实施减容增效改造。本文基于减容增效目标,开发适用于枯水期小流量的超低比转速轴流式转轮叶片,并解决了若干关键理论与技术难题。
1 枯水期不能发电原因及减容增效策略
水轮机设计工况为无撞击进口与法向出口。但设计工况只对应于某一水头和流量,实际运行中,由于水库水位及外界负荷的变化,水头和流量经常变化,致使水轮机经常偏离最优工况运行,产生进口撞击损失,使得尾水管动能回收量降低,效率下降。偏离设计工况越远,效率下降得越多。
1.1 枯水期小流量下不能发电的原因
图1为原转轮运行在设计工况点(简称Ⅰ工况点,其参数带角标“ ′”)时出口环量为零的圆柱面上翼型进出口速度三角形示意图,图中还标出流量过小不能发电工况点(简称Ⅱ工况点,其参数带角标“″”)在同一圆柱面上翼型进出口速度三角形。进口绝对速度的大小决定于水头H且恒定,故进口绝对流速v″1=v′1(下标“1”表示进口参数),其方向决定于导叶开度α,小流量下导叶开度减小,故α″1<α′1;圆周速度的大小决定于电网频率,其方向不变,故u″1=u′1=u″2=u′2(下标“2”表示出口参数);据圆柱层间无关性假设可知,进出口轴面速度的大小和方向应相等,故v′m2=v′m1、v″m2=v″m1;轴流定桨式转轮叶片安放角β无法调节,故β″2=β′2。
由图1b可知,圆周方向分流速v″u2过大,则出口环量Γ″2也过大;因ΔΓ″=Γ″1-Γ″2过小,则由水轮机基本方程式[4]可知,在H″和角速度ω″固定的情况下,效率η″s就会急剧下降,当流量下降到一定值时,过小的η″s会导致水轮机带不上负荷,此为小流量下不能发电的主要原因。另外,v″u2过大也将导致尾水管能量回收量变小,不仅降低了效率,还导致机组工作不稳定[5]。由图1a可以看出,β″1<β′1,即转轮运行在Ⅱ工况点时有较大的负撞击,将产生较大水力损失[6],使效率降低。

(a)进口速度三角形
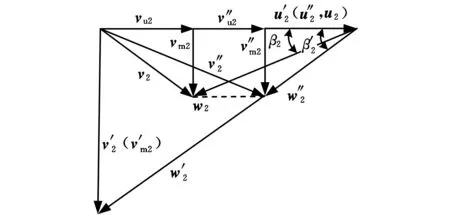
(b)出口速度三角形图1 原转轮和新转轮在Ⅰ、Ⅱ工况点进出口速度三角形
1.2 减容增效策略
基于减容增效目的,另外装备一个与现有过流通道及转速兼容的、适用于小流量的低比转速轴流定桨式转轮,使之在枯水期也能正常发电。新转轮的部分水力参数和机组参数,如H、n(转速)、b0(导叶高度)、D1(标称直径)、db(轮毂直径)与原转轮一致。丰水期和枯水期分别装备原转轮和新转轮,此方案方便可行且成本较低。
由于H和ω均为定值,由水轮机基本方程式可知,欲使新转轮在Ⅱ工况下的效率接近或达到原转轮在Ⅰ工况下的效率,应使新转轮在Ⅱ工况下进出口速度环量差接近或达到原转轮在Ⅰ工况下的进出口速度环量差,即ΔΓ≈ΔΓ′(未带上角标的为新转轮Ⅱ工况点参数),故2πrvu1-2πrvu2≈2πrv′u1-2πrv′u2(r为计算圆柱面半径,以下取等号),又由于v′u2=0,所以vu2=vu1-v′u1。
由上述分析及图1可得,原转轮和新转轮分别运行在Ⅰ工况点和Ⅱ工况点时在同一圆柱面上的一些参数关系:
v1=v″1=v′1
u1=u″1=u′1=u2=u″2=u′2
vm1=vm2=v″m1=v″m2
α1=α″1<α′1β1=β″1β2<β′2=β″2
由图1b可知,vu2远小于v″u2。当新转轮叶片进口安放角设计成约等于进水角时,液流进口无撞击或有较小正撞击,可克服或减弱原转轮在Ⅱ工况下所存在的问题。
2 进出口轴向流速及环量沿半径分布规律
2.1 进出口轴向流速沿半径分布规律
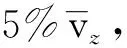
(1)
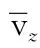

图2 轴向流速分布规律
2.2 进出口速度环量沿半径分布规律
新转轮在Ⅱ工况点进出口速度环量分布规律如图3所示,原转轮在轮毂圆柱面上出口速度环量为零[7],当流量从Q′减至Q时,该圆柱面上叶片进水角从β′1减至β1,出口速度环量由零增加至2πrvu2(记为Γ0),故新转轮的出口速度环量应在原转轮的出口速度环量分布规律上叠加一正值Γ0。经分析推导可知[4],转轮出口速度环量沿半径分布规律和进口速度环量沿半径分布规律如下:
(2)
(3)
式中,Γ2为转轮出口速度环量;Γ1为转轮进口速度环量;δΓ为出口环量在轮缘和轮毂间的差值;n′110为原转轮最优单位转速。

图3 进出口环量分布规律
3 计算机辅助水力设计关键技术
笔者开发的水力设计CAD软件,包括“水力计算模块”、“资料及数据处理模块”、“图形创建模块”及“系统管理和帮助模块”。采用Visual C++开发“水力计算模块”,该模块根据所输入的基本参数,以人机交互方式进行数值计算,获得翼型骨线离散数据。设计中用户可及时参阅“资料及数据处理模块”中各种数据、图表和实验曲线,并将计算结果与实验结果及设计经验作比对,作出取舍或评判。利用MFC对AutoCAD和UG进行二次开发,编制“图形创建模块”,该模块接受翼型骨线数据,自动生成叶片表面光滑性检查图和木模图,并生成转轮叶片三维模型。
3.1 翼型展开图向计算流面圆柱面转化技术
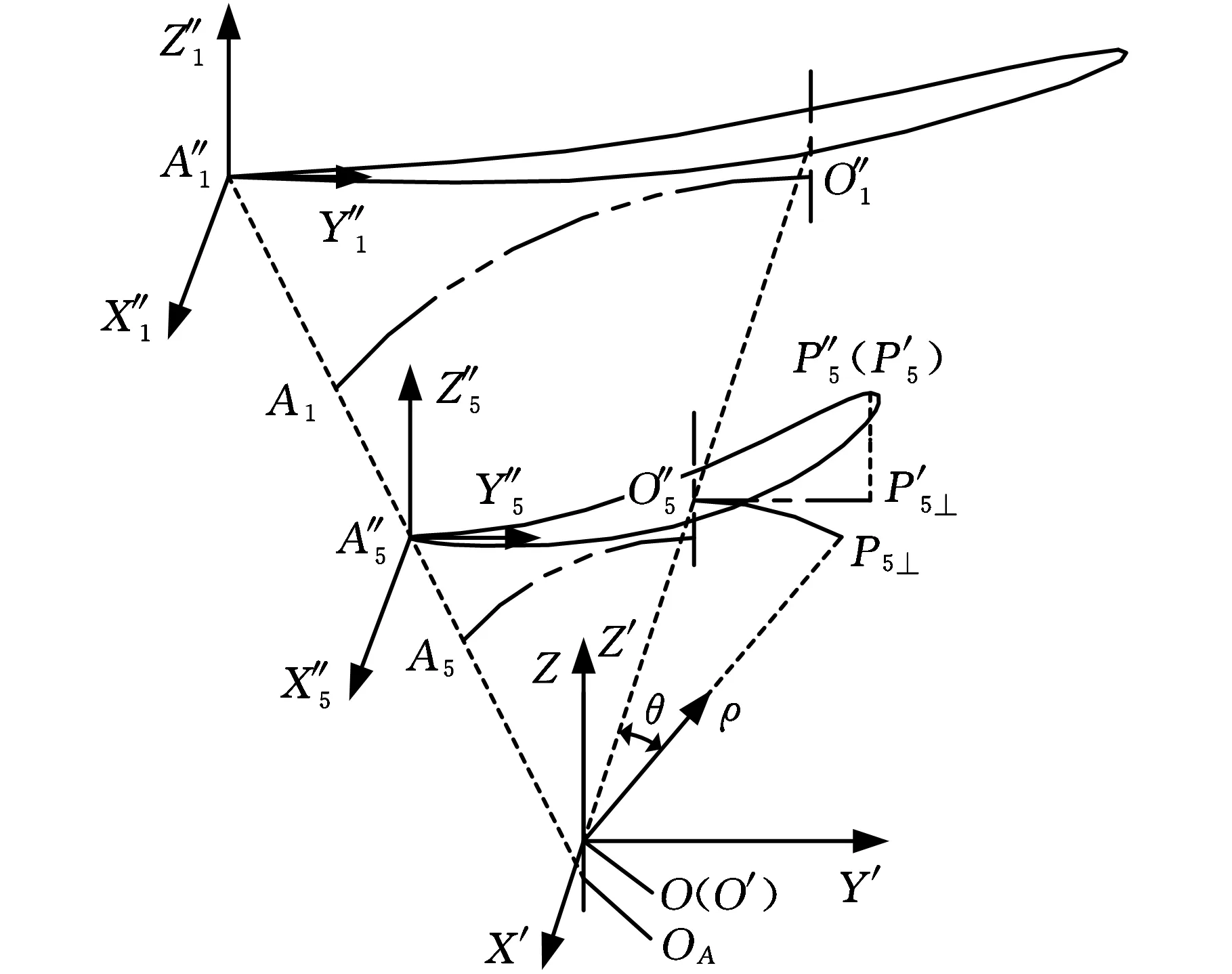
图4 翼型展开图离散点向计算流面圆柱面转化
水力计算所得为展开的翼型表面上若干个离散点的坐标值,叶片三维建模时,需将这些点转化为翼型计算流面所在圆柱面上的坐标值。根据翼型转动轴线位置确定规律[4],各翼型转动轴线的连线及翼型出口边的连线垂直于转轮轴线。如图4所示,以翼型流面1、5为例,翼型转动轴线O″1O″5垂直于转轮轴线,并交转轮轴线于O点;翼型出口边A″1A″5垂直于转轮轴线,并交转轮轴线于OA点。翼型流面2、3、4的转动轴线O″i(i=2,3,4)和翼型出口边A″i分别位于O″1O″5和A″1A″5上。以第5流面翼型为例,其计算流面圆柱面半径为r5,如图4所示,A″5X″5Y″5Z″5为水力计算所用坐标系,原点在翼型出水点;平移坐标系O′X′Y′Z′各轴平行于坐标系A″5X″5Y″5Z″5各轴,Z′轴与转轮轴线重合,且其原点在Z′轴与翼型转动轴线O″1O″5的交点上。采用坐标仿射变换原理[8],可将翼型上一离散点P″5在A″5X″5Y″5Z″5中坐标值变换为在O′X′Y′Z′中的坐标值,变换计算如下:
(4)
其中,(x″o′,y″o′,z″o′)为O′在A″5X″5Y″5Z″5中坐标值。

(5)
同理可推出1~4流面翼型上离散点在Zθρ柱面坐标系中的计算公式。
3.2 曲线智能延伸技术
水力计算获得若干个展开的翼型断面,二次开发AutoCAD绘制光滑性检查图和木模图时,这些断面采用3次Spline曲线拟合方法可方便绘制,但由于轮缘和轮毂翼型断面无法进行水力计算,其几何参数及光滑性检查曲线难以直接获取,所以本文根据拟合曲线抛物线边界条件,采用二次曲线[9],依据已拟合曲线的趋势外推预测,将各曲线智能延伸至轮缘和轮毂。二次曲线趋势外推预测模型为
(6)
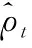
用最小二乘法确定待定参数为
(7)
式中,ρt为t点的序列观察值。
根据水力计算所得翼型断面数据,采用式(7)计算待定参数。依据预测模型式(6),可计算出轮缘和轮毂处点的预测值。
4 实例设计
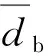

图5 转轮三维模型图6 转轮实物图
5 结论
(1)基于减容增效策略设计的超低比转速轴流式转轮,其转轮类型和部分基本参数与原转轮相同,但叶片出口处允许有较常规设计值大的正向环量,该叶片叶栅稠密度较大,叶片数较多,其汽蚀性能优于原转轮。
(2)采用计算机辅助水力设计技术,缩短产品设计研发周期,提高了设计效率;再次开发性强;三维模型的开发为二维识图带来方便,并为CFD分析和数控制造提供了基础。
(3)设计实例成功应用于电站,表明运行策略、方法正确可行,达到枯水期小流量下轴流定桨式水电站减容增效改造目标。
[1] 刘有余.超常规轴流式转轮叶片水力设计方法研究[D].兰州:兰州理工大学,2004.
[2] 廖伟丽,姬晋廷,肖微,等.轴流转桨式水轮机转轮进口前流场的数值分析[J].农业工程学报,2007,23(10):106-111.
[3] Singh P, Nestmann F. Experimental Investigation of the Influence of Blade Height and Blade Number on the Performance of Low Head Axial Flow Turbines[J]. Renewable Energy,2011,36(1):272-281.
[4] 刘大恺.水轮机[M].北京:中国水利水电出版社,1996.
[5] 陈庆光,吴玉林,刘树红,等.轴流式水轮机全流道内非定常空化湍流的数值模拟[J].机械工程学报, 2006,42(6): 211-216.
[6] Liu Pengfei. A Computational Hydrodynamics Method for Horizontal Axis Turbine-panel Method Modeling Migration from Propulsion to Turbine Energy[J].Energy,2010,35(7):2843-2851.
[7] Lieser J A, Lohmann D, Rohardt C H. Aero Acoustic Design of a 6-bladed Propeller[J]. Aerospace Science and Technology, 1997, 1(6):381-389.
[8] Moustris G, Tzafestas S G. Reducing a Class of Polygonal Path Tracking to Straight Line Tracking via Nonlinear Strip-wise Affine Transformation[J]. Mathematics and Computers in Simulation, 2008,79(2):133-148.
[9] Liu Xuqing, Wang Dongdong, Rong Jianying. Quadratic Prediction Problems in Multivariate Linear Models[J]. Journal of Multivariate Analysis, 2009,100(2):291-300.
[10] 李冬,王树杰,王超.潮流能水轮机叶片实验原型快速制造方法研究[J].中国机械工程,2009,20(21):2541-2544.
——“AABC”和“无X无X”式词语
——目镜套筒

