基于二维非绝热模型的脉管损失机理研究

植晓琴，邱利民，甘智华，俞益波，曹强

（浙江大学 制冷与低温研究所，浙江 杭州，310027）

脉管制冷机具有低温端无运动部件的优点，近年来，在空间技术、国防军事、医学医疗等领域得到广泛应用[1]。作为制冷机的核心部件之一，脉管的理想功能是将冷端PV功无损失地传到热端，并且使这一过程无熵产[2]。而实际上，脉管内不可避免地存在管壁与气体之间的穿梭损失、管壁导热损失、边界层泵气损失、气体自身导热损失、气体温度非均匀（冷热混合）损失、环流损失以及阻力损失等[3−6]。Yang[5]计算出仅脉管内的穿梭和泵气损失占毛制冷量的20%～60%，严重削弱了脉管的制冷性能。研究表明：脉管损失和其结构尺寸密切相关，合适的脉管体积和长径比可以降低其损失，提高膨胀效率[7−9]。与回热器相比，脉管仅为1根空管，作用机理看似简单，目前与之相关的研究也较少，并存在一些不足。Kirkconnell等[9]的实验结果表明脉管体积越大损失越小，但由于实验范围有限，并没有找出脉管的最佳体积。Junseok等[10]通过实验发现体积小的脉管虽然能提高电功转化效率，增大压比，但脉管内膨胀损失产生的负效应更大，反而使整体性能变差。该实验中只采用了3种不同体积的脉管，并且改变了长径比，无法确定哪一个因素对制冷性能产生了影响。Jeheon等[11]推导了脉管体积的计算公式，对脉管设计有一定的指导意义，但该模型进行了过多简化，不可避免地引起计算误差。总体来说，关于脉管结构与膨胀效率的研究很少，也没有研究指出脉管结构对其热损失的影响机制。寻找最佳脉管结构尺寸需要进行大量尝试，探索其损失机理需要对内部气体的瞬态参数进行分析，实验方法不适用。而脉管内温度分布和流动的非线性特征也使得理论分析较困难。而数值模拟方法操作方便，并且对计算结果更容易分析。目前，脉管的数值模拟方法多为一维或假设管壁绝热，包括脉管制冷机设计软件Sage也是一维模型。一维模型忽略了管内的温度非均匀性和二次流，不能计算由附加环流以及温度不均匀引起的热损失。而常用的回热器设计软件Regen在计算脉管制冷量时，仅采用经验性的脉管系数对其膨胀效率进行估算，脉管的体积则根据经验取冷端扫气容积的3～5倍。以上对脉管损失考虑不足都会使脉管的结构设计偏离实际最佳值，因此，采用更符合实际的数值模型研究脉管的结构尺寸对脉管制冷机的设计具有重要的指导意义。为此，本文作者结合实际中脉管的非绝热性（管壁与管内气体间存在非绝热换热损失）和管内气体温度的非均匀性，基于 CFD方法建立80～300 K温区脉管的二维非绝热模型，研究一定冷端扫气容积下与之匹配的最佳脉管体积，并根据脉管内的温度分布现象分析脉管体积对其热损失的影响机理。

1 脉管的CFD模型

1.1 物理模型

本文建立的脉管模型参数来自现有的单级斯特林型脉管制冷机，包括冷端连管、冷端换热器、脉管、热端换热器和热端连管，如图1（a）所示。绝热模型假设无壁厚，即忽略管壁与管内气体间的换热；非绝热模型中脉管和两端换热器壁厚为0.34 mm，即考虑管壁与管内气体间的换热。冷、热端换热器与连管之间采用锥形结构过渡，内部填料直径为0.18 mm的铜丝网。脉管体积的取值Vpt与冷端扫气容积Vexp关系如下：

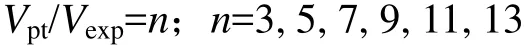
其中：冷端扫气容积Vexp指1个周期内单向流入（或流出）脉管冷端的气体总体积，此处为2.86×10−6m3。所有脉管的长径比固定为5，各部件参数如表1和表2所示（其中：Dpt，Lpt和Vpt分别为脉管直径、长度和体积）。

脉管的网格模型如图1（b）所示。在锥形过渡区采用三角形网格，其他部位采用四边形网格。为了更准确地描述边界层流动特性，对脉管近壁面区域网格进行加密处理。网格总数为3 472～4 280，网格的最大长宽比小于3。

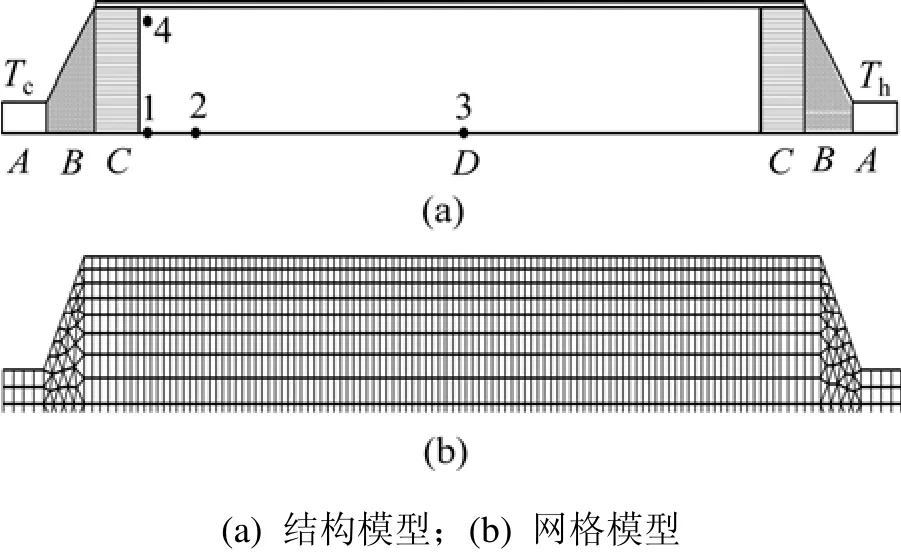
图1 脉管结构示意图Fig.1 Schematic of pulse tube model

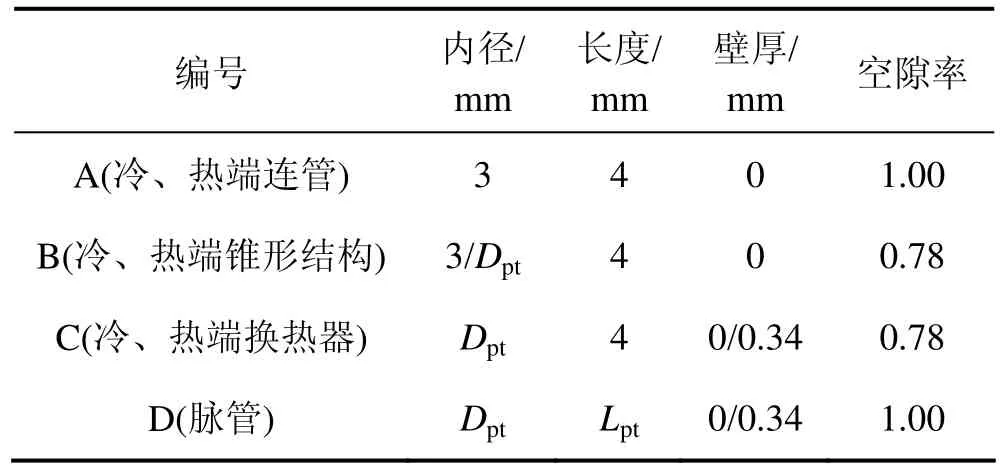
表1 脉管模型中的结构参数Table 1 Structural parameters of pulse tube model

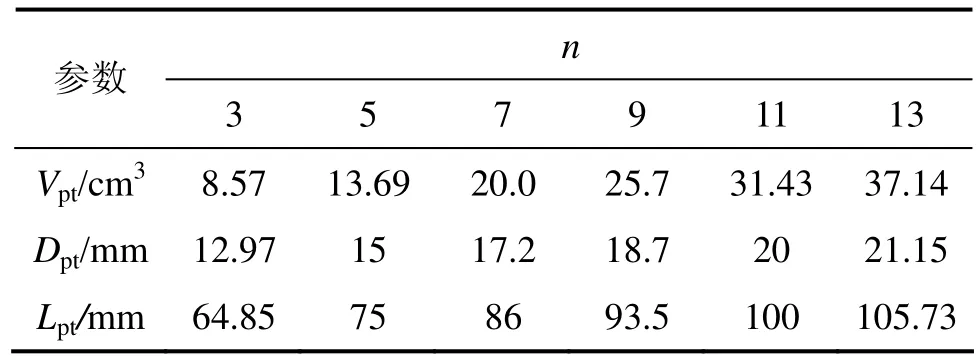
表2 图1中D段脉管尺寸（长径比Lpt/Dpt=5）Table 2 Pulse tube dimension for part D in Fig.1

在80～300 K温区，工质氦气作理想气体处理。充气压力为2 MPa，工作频率为40 Hz。进口边界条件采用正弦压力波，温度为80 K；出口边界条件采用正弦质量流，温度为300 K，表达式如下：

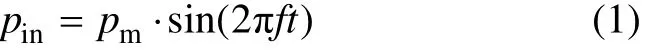
其中：pm为周期压力振幅；f为运行频率；mamp为周期质量流振幅；φ为进口压力波与出口质量流之间的相对夹角。对于所有模型，以上参数均为定值。冷、热端换热器采用多孔介质模型，假设温度恒定，分别为80 K和300 K。换热器和进出口连管壁面均为等温边界条件，脉管外壁面与外界为绝热边界条件。

1.2 基本控制方程

本模型流动区域分为多孔介质区域（冷热端换热器、锥形结构）和非多孔介质区域（进出口连管和脉管），求解的连续性方程、动量方程和能量方程如下[12−13]：

其中：φ为多孔介质的空隙率；Sx和Sy分别表征轴向和径向上由阻力损失引起的动量损失；kf和ks分别为气体和固体的导热系数。对于非多孔介质区域，φ=1，

Sx（y）=0；对于多孔介质区域，阻力源项表示如下：

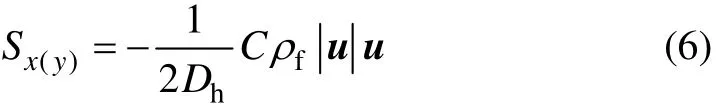
Dh为丝网填料水力直径；C为丝网填料阻力系数。目前，关于丝网填料径向的阻力特性研究很少。假设丝网阻力各向同性，径向和轴向的阻力系数均采用文献[14]中推荐的经验公式：

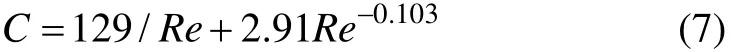
其中：Re为雷诺数。本文选择适合较宽范围雷诺数的标准k-ε湍流模型计算。利用有限体积法采用全隐格式离散控制方程，求解器选择压力和速度耦合的PISO算法，离散格式对流项取二阶迎风格式，扩散项为中心差分，对源项进行线性化处理；残差收敛标准气体能量项和填料能量项为10−6，其他参数均为 10−3。当脉管冷端温度和焓流连续 10个周期内的变化值均小于1%时，认为计算稳定。1个周期内的时间步为100，所有模型大约计算200个周期后趋于稳定。

1.3 后处理参数

在膨胀过程中，若各种损失引起的不可逆熵产越小，则脉管的焓流越大，制冷量越大。基于CFD模型的计算结果，1个周期内脉管的声功和焓流进行如下处理：

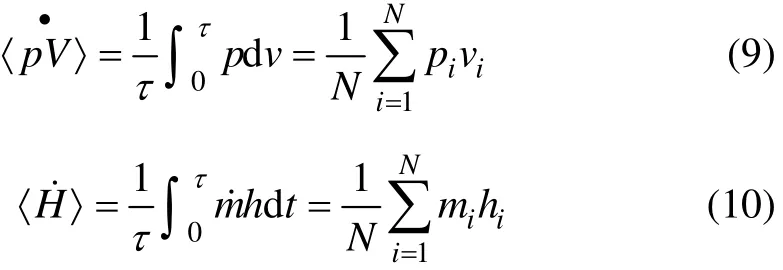
其中：τ为时间；N为1个周期内迭代的时间步数；pi，vi，mi和hi分别为第i个时间步的压力、体积流速、质量流速和比焓。

2 结果分析

2.1 脉管膨胀效率及损失分布

不同体积的脉管膨胀效率计算结果如图2所示。从图2可见：对于绝热模型，脉管的最佳体积为冷端扫气容积的5倍，对应的膨胀效率为77.3%；当脉管的最佳体积为冷端扫气容积的3～5倍时，脉管膨胀效率随体积的增大而增大；为5～11倍时，膨胀效率随着体积增大开始缓慢减小，可以推断在此范围内脉管已经起到了较好的轴向绝热和气流隔离效果；随着体积的增大，其效率主要受阻力损失的影响；当大于 11倍时，脉管膨胀效率急剧减小。这是因为随着脉管体积的增大，过渡区锥度也变大，在脉管热端造成了较强的射流损失；此外，较大的体积也增大了脉管的阻力损失。

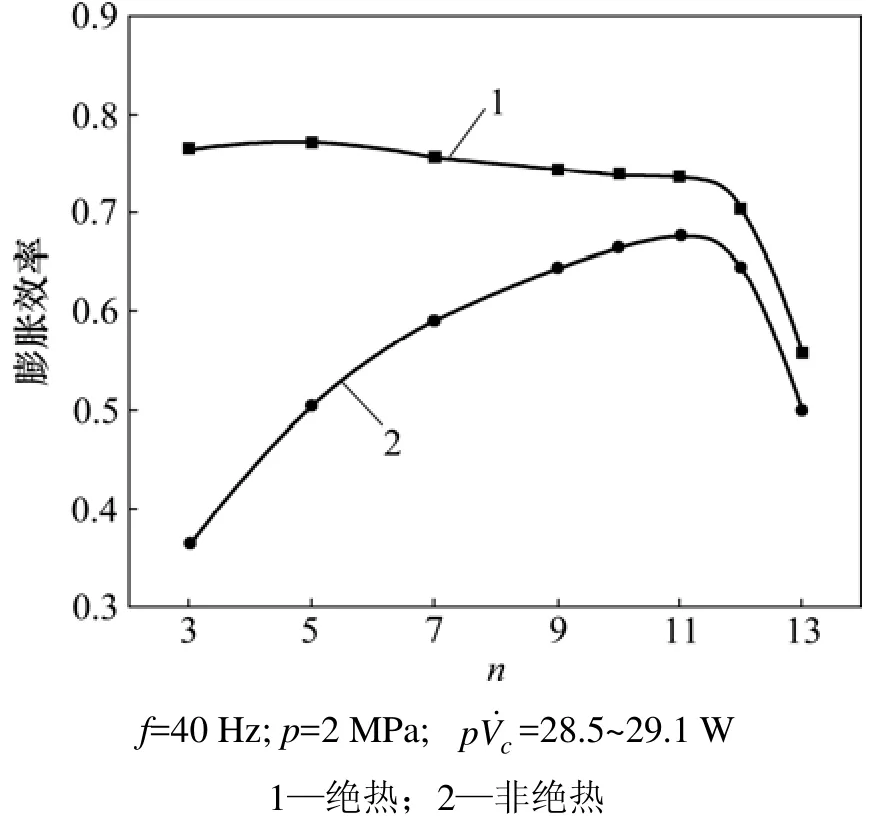
图2 体积比n与膨胀效率的变化关系Fig.2 Relationship between expansion efficiency and volume ratio

对于非绝热模型，脉管的最佳体积范围为冷端扫气容积的10～11倍，11倍体积对应的最高膨胀效率为67.7%，与绝热模型相差较大。图 3所示为非绝热模型管壁热损失随脉管体积的变化关系。从图3可以看出：在脉管体积为冷端扫气容积的3～11倍时，脉管效率主要受管壁热损失的影响；在5倍以下时，管壁热损失可达总损失的 50%以上；当大于 11倍时，增大体积对热损失已无明显影响，反而使得脉管内射流损失急剧增大，与绝热模型有相同趋式。可见：与绝热模型相比，实际脉管需采用更大的体积减小管壁热损失，提高其膨胀效率。在相同条件下，非绝热模型计算的最佳脉管体积比理想绝热模型的大。假设冷端声功和回热器冷端焓流相同，若以绝热模型的最佳体积5倍来设计脉管，则与实际非绝热模型的最佳体积11倍相比，80 K的制冷量将比实际最佳值降低4.9 W，对应的脉管效率将减小 17.2%。因此，传统观点认为的脉管体积取冷端扫气体积的3～5倍以及一维或绝热模型都不能准确地给出脉管的最佳膨胀体积。

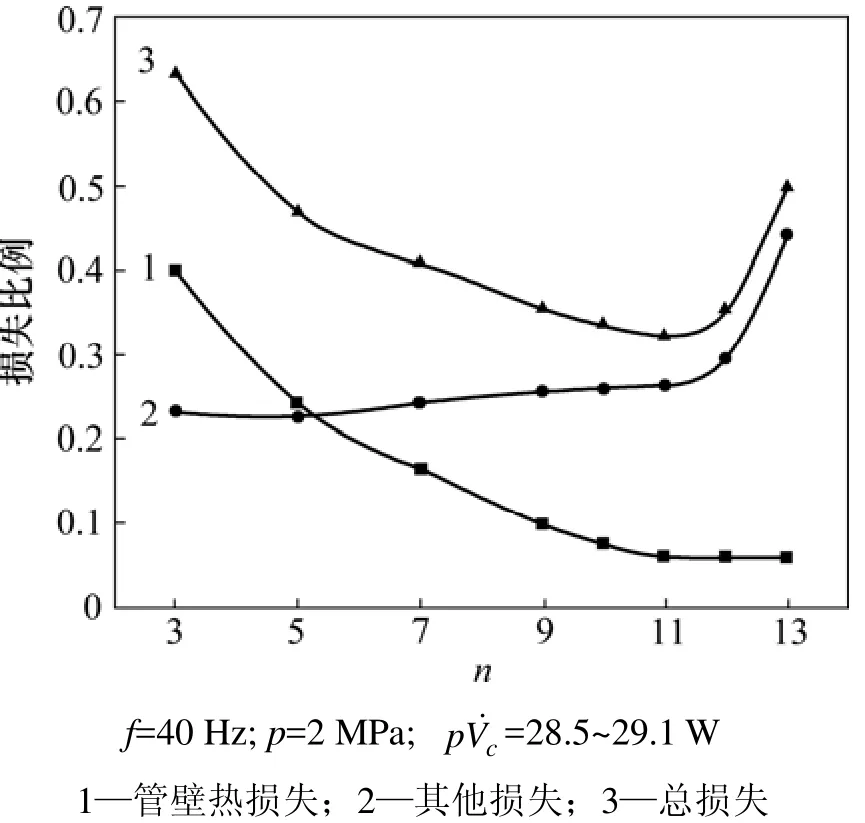
图3 体积比n与管内损失的变化关系（非绝热）Fig.3 Relationship between pulse tube losses and volume ratio in non-adiabatic case

2.2 不同体积脉管内气体温度分布特性与热损失分析

图4中a，b，c和d点表示脉管冷端进口压力的4个状态，图5给出了其中a和c（分别代表压缩过程、膨胀过程）状态下脉管内的温度分布。对于理想的脉管，气流为层流状态，同一截面上温度处处相等。然而，在实际脉管中（如图 5所示），由于黏性边界层的作用等温线在近壁处产生明显的弯曲，在近壁以外的主流区域，由于流动不均匀，等温线也出现弯曲。同一截面上温度的非均匀性无疑增加了管内气体之间的不可逆换热损失。

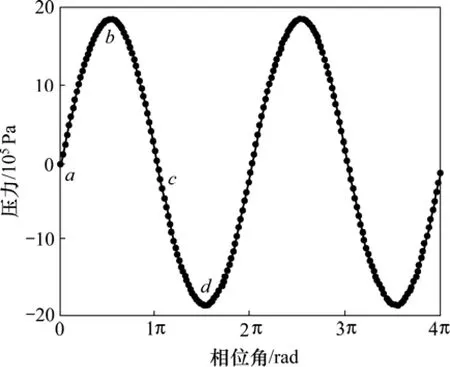
图4 脉管冷端进口压力波Fig.4 Inlet pressure wave at pulse tube cold head

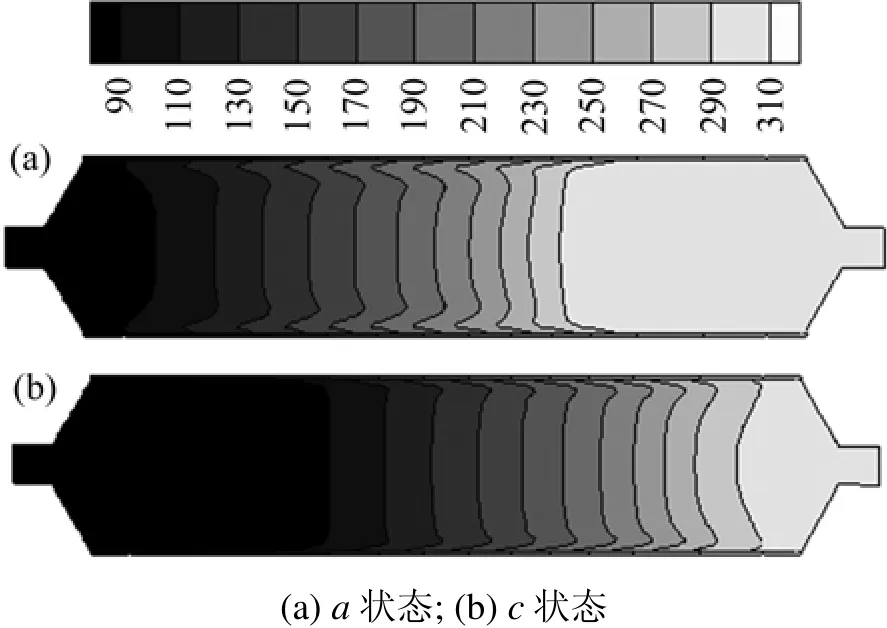
图5 不同时刻脉管内的温度分布情况Fig.5 Temperature distribution at different moments

与斯特林制冷机相似，脉管中的热损失主要包括气体进、出边界层产生的泵气损失和气柱移动导致的穿梭损失[15]。穿梭损失和泵气损失与气柱位移长度、管壁温度梯度有关[5−6]。对于相同的冷端扫气容积，较小体积的脉管内气柱位移大，同时较短的脉管温度梯度大，两者都会使气柱运动时气体与管壁的温差变大，增大穿梭损失。同样，管内气体温度梯度高且气柱的位移大，导致边界层内气体与管内主流气体温差较大，从而产生更大的泵气损失。

图6所示为状态a和c时，不同体积脉管内近壁线（距管壁0.1 mm，属于边界层内）和轴线上的温度分布。从图6可见：在压缩、膨胀过程中，3倍体积脉管的近壁线和轴线的平均温差分别为 15.3 K和 18.3 K，而11倍体积脉管内两者的温差分别为5.5 K和8.6 K，明显比3倍体积的脉管温差小，11倍体积脉管内的温度分布更均匀。图7所示为a和c状态时，不同体积脉管内近壁线和壁面的温度分布。从图7可见：对于3倍体积的脉管，气体与壁面的温差分别为13.1 K的12.7 K，远大于11倍体积脉管内两者的温差。由上可知：3倍体积的脉管具有更大的泵气损失和穿梭损失。

表3列出了非绝热模型中不同体积脉管内的平均温差。当n＜11时，随着体积的增大，脉管内各项温差均逐渐变小，可见：较小体积脉管内温度存在更大的非均匀是其效率低于较大体积脉管效率的内在原因；而当 n=13时，在压缩过程中，由于热端射流的影响，脉管轴线与近壁处气体的温差变大，造成效率急剧减小。

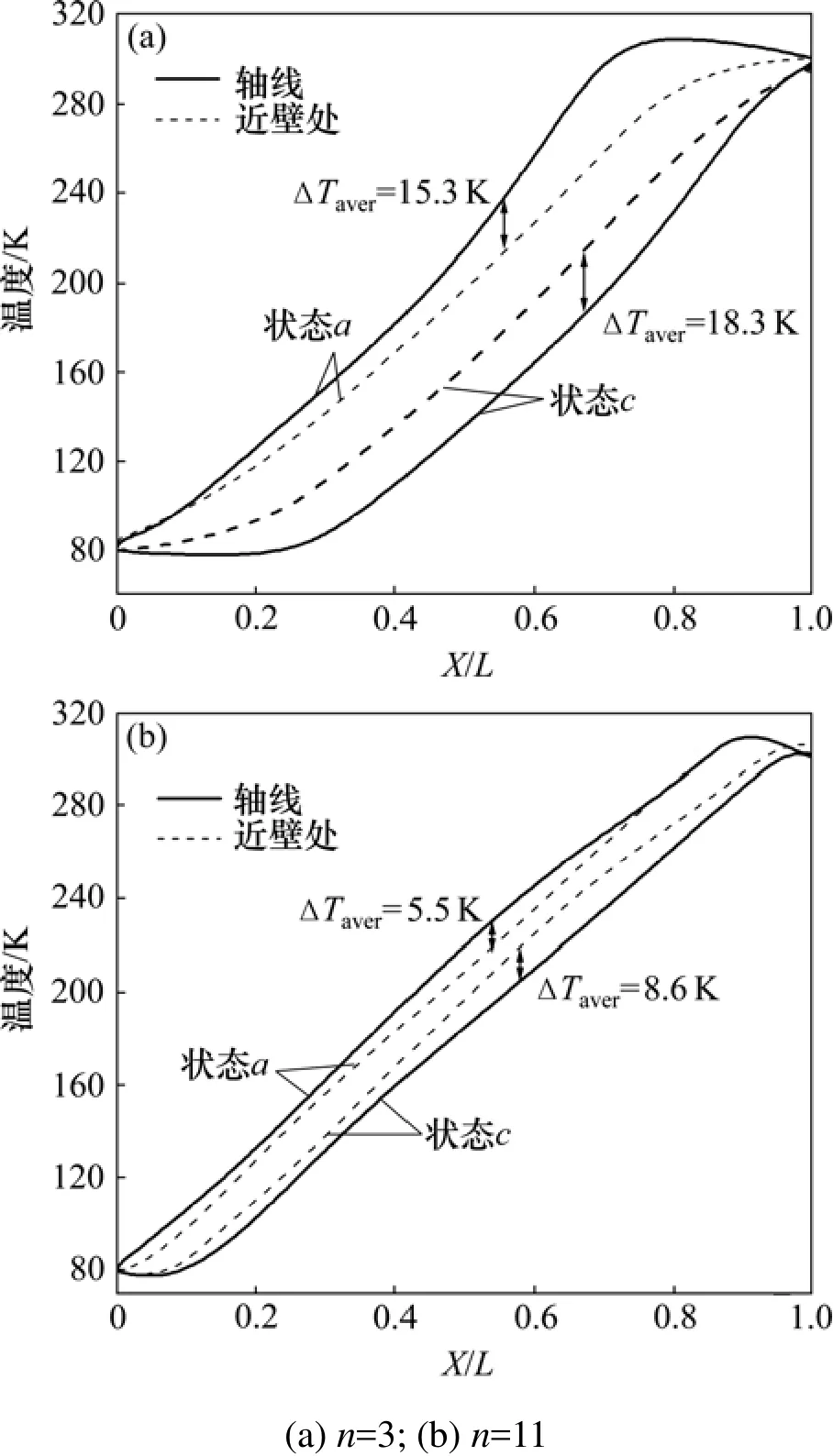
图6 非绝热下状态a和c时轴线和近壁处温度分布Fig.6 Temperature distribution at axes and near wall region in non-adiabatic case at status a and c

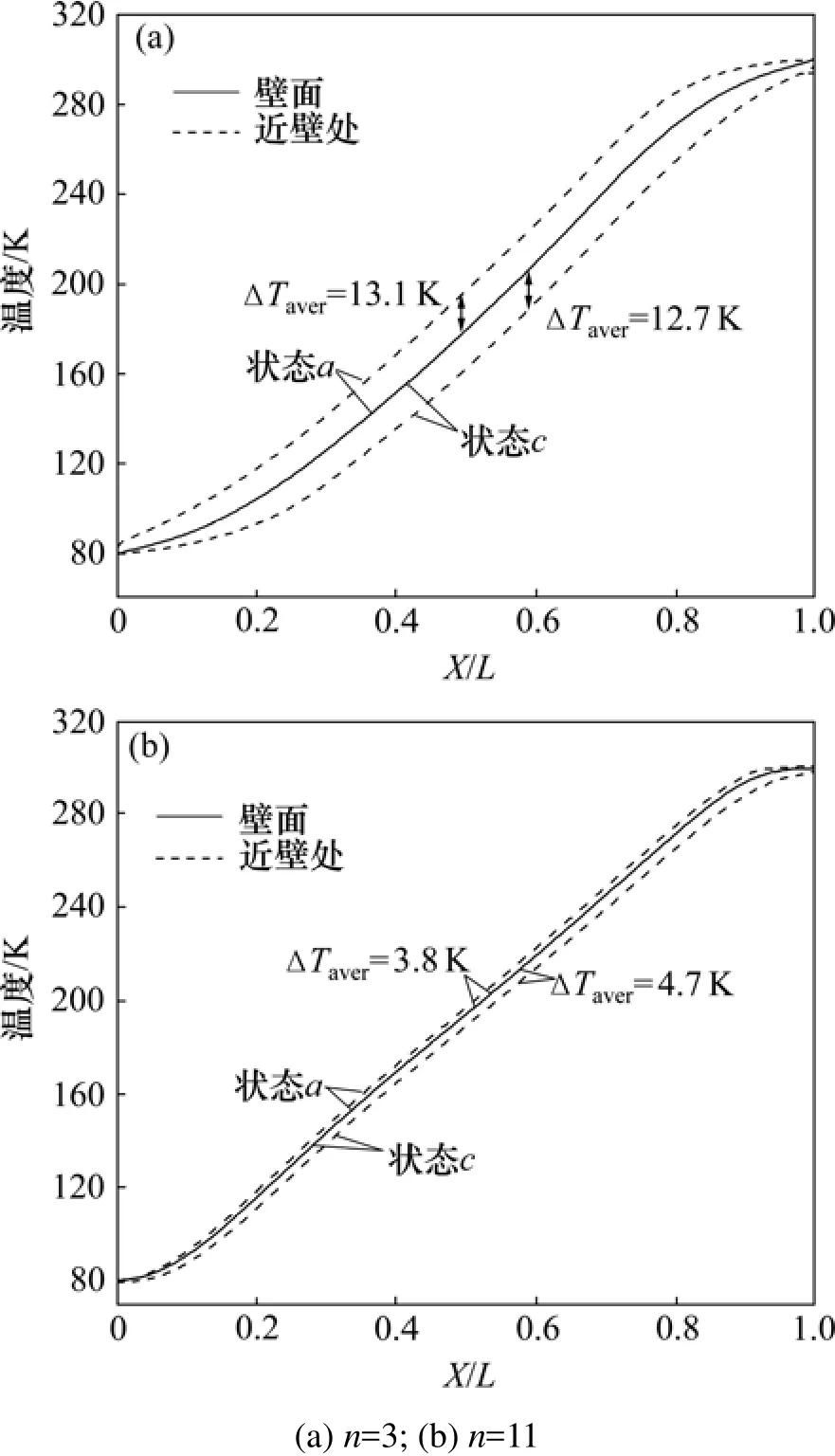
图7 非绝热下状态a和c时壁面与近壁处的温度分布Fig.7 Temperature distribution at wall and near wall region in non-adiabatic case at status a and c

表3 非绝热模型中不同体积脉管内的平均温差Table 3 Average temperature difference of non-adiabatic pulse tubes with different volumes K

图8所示为绝热条件下3倍体积脉管内的温度分布情况。从图6和图8可以看出：对于相同体积的脉管，绝热模型内气体的温差要比非绝热模型小得多；在压缩、膨胀过程中，绝热模型内轴线和近壁面的平均温差分别为0.7 K和1.6 K，同一截面上气体的温度更均匀。可见：非绝热模型中管壁与气体的换热影响了管内气体的温度分布，使得近壁面气体与内部气体的温差变大。因此，管壁的非绝热不仅带来了穿梭热损失，同时增大了近壁面的泵气损失。而一维或绝热模型无法反映这种温差以及因温差所产生的热损失。

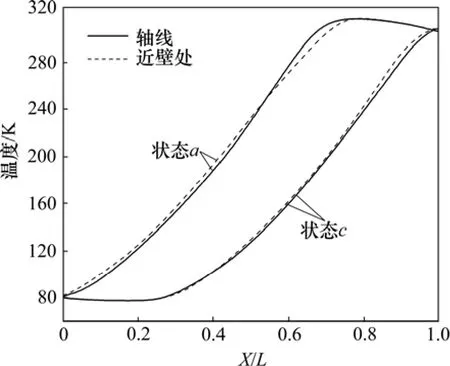
图8 绝热下状态a和c时轴线与近壁处的温度Fig.8 Temperature distribution at axes and near wall region in adiabatic case at status a and c

3 结论

（1）建立了 80～300 K温区脉管的二维非绝热模型。通过计算得出实际非绝热脉管的最佳体积范围为冷端扫气容积的10～11倍，不同于绝热模型得出的3～5倍；管壁与气体间非绝热损失的存在使得脉管要达到较高的膨胀效率需采用更大的体积。脉管的非绝热损失可占其总损失的50%以上，不可忽略，传统的一维或绝热模型都不能正确地给出脉管的最佳体积。

（2）在研究范围内，体积较小的脉管管壁与管内气体存在较大的温差；同时，管内气体具有更强的温度不均匀性，因而导致更大的热损失，致使其脉管效率降低。

（3）与绝热脉管相比，非绝热脉管管壁与管内气体的换热不仅造成穿梭损失，同时，改变了近壁气体与中心气体的温差，增大了近壁面的泵气损失。

[1]Radebaugh R.The development and application of cryocoolers since 1985[C]//Cryocoolers 12.New York:Kluwer Academic/Plenum Press,2003:858−870.

[2]Radebaugh R.Thermodynamics of regenerative refrigerators[J].Generation of Low Temperature and It’s Applications,2003:1−20.

[3]蒋彦龙,陈国邦.脉管制冷机中的直流流动[J].世界科技研究与发展,2006,28（5）:62−68.JIANG Yan-long,CHEN Guo-bang.DC flow and its suppression in pulse tube cooler[J].World Sci Tech R&D,2006,28（5）:62−68.

[4]Shiraishi M,Murakami M,Nakano A.Visualization of secondary flow in an inclined double-inlet pulse tube refrigerator[C]//Cryocoolers 14.Colorado:ICC Press,2007:277−284.

[5]YANG Lu-wei.Shuttle loss in pulse tubes[C]//Cryocoolers 11.New York:Kluwer Academic/Plenum Press,2001:353−362.

[6]YANG Lu-wei.Theoretical analysis of refrigeration and losses in a pulse tube[C]//Advances in Cryogenic Engineering.New York:AIP Press,2000,45:175−182.

[7]吴明,何雅玲,陶文铨,等.最佳脉管长径比优化设计的理论分析及数值模拟[J].西安交通大学学报,2002,36（3）:230−232.WU Ming,HE Ya-lin,TAO Wen-quan,et al.Optimum design of the length to diameter ratio of the pulse tube by theory and numerical simulation[J].Journal of Xi’an Jiaotong University,2002,36（3）:230−232.

[8]党海政,梁惊涛,周远.高频微型同轴非金属脉冲管制冷机几何尺寸优化的实验研究[J].低温工程,2005（2）:1−4.DANG Hai-zheng,LIANG Jing-tao,ZHOU Yuan.Investigation on optimization of the dimensions of high frequency miniature co-axial nonmetallic pulse tube cryocooler[J].Cryogenics,2005（2）:1−4.

[9]Kirkconnell C S,Soloski S C,Price K D.Experiments on the effects of pulse tube geometry on PTR performance[C]//Cryocoolers 9.New York:Plenum Press,1996:285−293.

[10]Junseok K,Sankwon J,Taekyoung K.Effects of pulse tube volume on dynamics of liner compressor and cooling performance in Stirling-type pulse tube refrigerator[J].Cryogenics,2010（50）:1−7.

[11]Jeheon J,Sankwon J.Optimal pulse tube volume design in GM-type pulse tube refrigerator[J].Cryogenics,2007（47）:510−516.

[12]ZHANG Xiao-bin,QIU Li-min,Gan Zhi-hua,et al.CFD study of a simple orifice pulse tube cooler[J].Cryogenics,2007（47）:315−321.

[13]俞益波.基于非热平衡的单级斯特林型脉管制冷机CFD模拟与实验研究[D].杭州:浙江大学能源工程学系,2010:28−35.YU Yi-bo.Numerical and experimental analysis of a Stirling-type single-stage pulse tube cryocooler with thermal non-equilibrium model[D].Hangzhou:Zhejiang University.Department of Energy Engineering,2010:28−35.

[14]Gedeon D.Sage Stirling-cycle model class reference guide[M].Athens:Gedeon Associates Press,2007:111−113.

[15]陈国邦,汤珂.小型低温制冷机原理[M].北京:科学出版社,2010:128−129.CHEN Guo-bang,TANG Ke.Refrigeration theory of miniature cryocoolers[M].Beijing:Science Press,2010:128−129.