高超声速二元机翼迟滞非线性热颤振
钮耀斌,王中伟
(国防科学技术大学 航天与材料工程学院,湖南 长沙,410073)
颤振问题是飞行器飞行中最有可能发生灾难性事故的气动弹性问题。在工程实际中,飞行器系统会存在各种非线性因素,降低飞行器的颤振速度,产生极限环、混沌等不稳定现象,严重影响飞行器的飞行稳定性和安全性[1−4]。气动弹性的非线性因素主要分为两大类:气动非线性与结构非线性。激波和气流分离等因素使得气动力产生了非线性,且随着马赫数的增大,非线性效应的影响增大。以往采用线性理论计算非定常气动力的方法已经不再适用。结构非线性的因素比较复杂:薄机翼会产生立方特硬非线性,即随着扭角的增加,刚度渐硬;失效的控制面会导致间隙非线性的出现;而高超声速飞行器大多采用全动尾翼结构,常常会同时存在间隙和摩擦机制,产生迟滞非线性特性。另外,对于高超声速飞行器,由于气动热的影响,整个飞行器结构都处于高温环境中,这将导致飞行器表面及内部产生热非线性变形。当系统具有非线性环节时,会呈现出极为复杂的运动形式,如极限环振荡、周期倍化分岔、混沌运动等不稳定现象。郑国勇等[5−6]采用一阶近似活塞理论计算非定常气动力,研究了带有立方非线性俯仰刚度二元机翼的气动弹性问题,得出了系统特定参数下的极限环颤振和混沌响应。方明霞[7]采用三阶活塞理论计算气动力,研究了高超声速机翼的迟滞非线性现象。McNamara等[8−9]研究表明,气动热对高超声速飞行器的气动弹性影响很大,不仅会降低材料的力学性能,在结构内部产生热应力而影响刚度,而且还会使结构产生热非线性变形,严重影响飞行器的气动弹性稳定性。但到目前为止,考虑气动热效应的高超声速机翼的非线性气动弹性问题研究的较少。Laith[10−11]采用三阶活塞理论计算气动力,研究了具有立方非线性机翼的热颤振现象。本研究采用三阶活塞理论计算非定常气动力,并考虑高超声速下气动加热的影响,对具有结构迟滞非线性的高超声速二元机翼进行热颤振分析。
1 模型与动力学方程
选取单位展长的高超声速二元机翼,其力学模型如图1所示。2个自由度分别为:沉浮自由度h,向下为正;俯仰自由度α,机翼前缘抬头为正。b为半弦长,弹性轴到重心的距离为xab,弹性轴到机翼中点的距离为ab,自由来流速度为U∞。
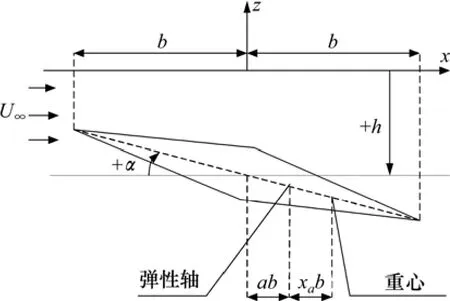
图1 二元机翼模型Fig.1 Model of two-dimensional airfoil
迟滞非线性广义力F(x)与位移和速度的关系可以表示为[12]:

其中:A和B为非线性系数。
由拉格朗日方程得到高超声速流中带迟滞非线性刚度系统的运动微分方程为:
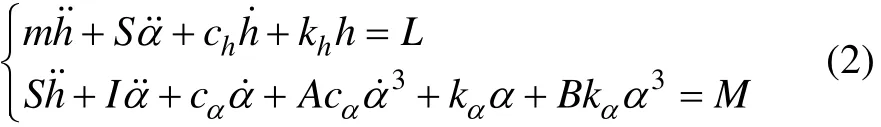

机翼的无量纲运动方程为:
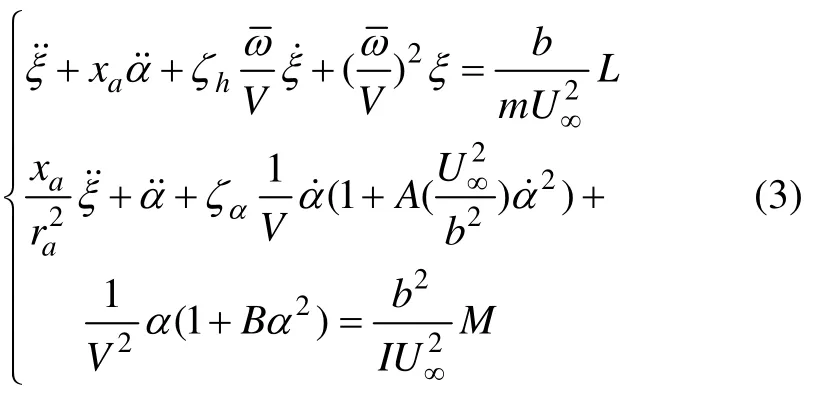
2 气动力与气动热
2.1 非定常气动力
对于高超声速机翼的非定常气动力,由于其结构较薄、三维效应较小,因此活塞理论仍然适用[13]。另外,在高马赫数下,三阶活塞理论与欧拉方法相差不大[14]。因此,本研究采用修正的三阶活塞理论计算机翼的非定常气动力:

其中:p为当地气流压强;p∞为来流压强;vz为翼面法向速度;c∞为来流音速;γ为空气动力修正因子;
机翼中线上任意一点的z方向位移用z(x,t)表示,则有:
对上表面,

对下表面,

其中:H(x,y)为机翼的厚度函数。
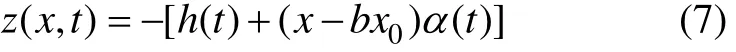
作用在机翼上的气动力和气动力矩可由下式求得:
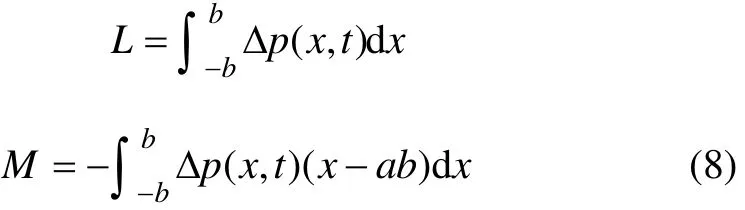
2.2 气动热及其对刚度的影响
飞行器的高超声速飞行带来了巨大的气动热,严重影响了飞行器的稳定性。驻点温度可以采用下式进行估算:
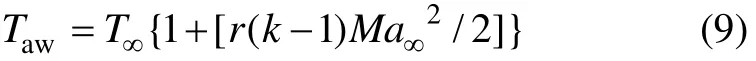
由驻点温度可得到气动加热对扭转刚度的影响[15]:
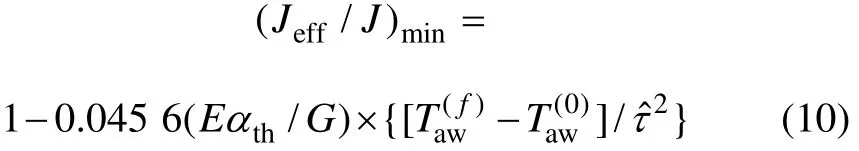
其中:J为室温下的扭转刚度;Jeff为气动加热下的有效扭转刚度;E为弹性模量;G为剪切模量;αth为热膨胀系数;为厚度比(即th/b,th为机翼中点处的厚度);分别为初始时刻和f时刻的驻点温度。
若初始时刻和f时刻的环境温度相同,则将式(9)代入式(10)可得到气动加热对扭转刚度的影响:

则考虑气动加热情况下俯仰方向的固有频率为:

3 数值仿真与结果分析
本研究以高超声速二元机翼为研究对象,进行热颤振分析,机翼沉浮和俯仰的固有频率比=0.5,其余参数如表1所示。
3.1 线性颤振速度
线性颤振的分析不考虑各种非线性因素,当飞行速度小于颤振速度时,系统稳定;当飞行速度大于颤振速度时,其振动发散导致结构破坏。

表1 二元机翼基本参数Table 1 Baseline parameters of 2-DOF airfoil
在不考虑非线性因素的情况下,运用三阶活塞理论计算气动力,并采用P-K法分析二元机翼的线颤振速度。得到在马赫数Ma=5,厚比比τ=0.1的情况下,高超声速气动加热系统的无量纲线颤振速度为vfT=387.59,而不考虑气动加热的影响时,其颤振速度为vf=432.36。可见,气动热效应使得机翼的线颤振速度下降达10.35%。
机翼的厚度比对机翼外部的气动加热有很大的影响,从而影响其颤振速度。图2所示为二元机翼无量纲热颤振速度随厚度比的变化趋势。
由图2可以看出:热颤振速度随机翼厚度比的增大而逐渐增大。这是由于增大厚度比 τ,机翼外部的气动热会有所下降,使得其扭转刚度有所增加,而提高了热颤振速度。
3.2 非线性热颤振分析
线性气动弹性系统在流速小于线性颤振速度时表现为振幅衰减运动;当流速高于线性颤振速度时表现为发散运动。非线性气动弹性系统则在小于或高于线性颤振速度时均表现为极限环振动,甚至出现混沌运动。
为考虑非线性热颤振系统参数大范围变化时的分岔问题,选俯仰角加速度正向通过为零时的点作为轨线与广义poincare截面的交点,即定义poincare截面为:
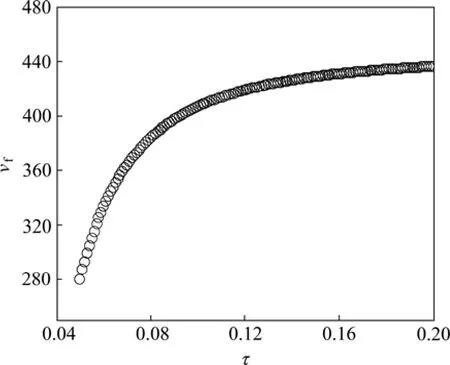
图2 热颤振速度vf随厚度比τ变化曲线Fig.2 Heat-flutter velocity with various thickness ratios

根据poincare截面,可得二元机翼响应振幅随来流速度变化的分岔图,如图3所示。
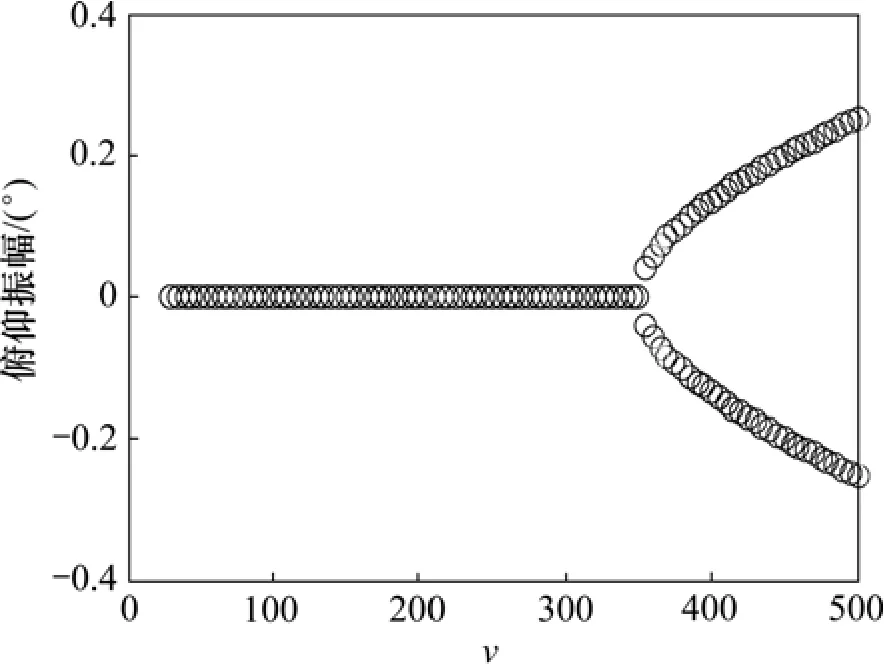
图3 响应振幅分岔图Fig.3 Bifurcation diagram of amplitudes
由图3可以看出:当无量纲来流速度为350.12(约为0.9倍线颤振速度)时系统出现分岔,系统响应由稳定状态变为极限环振荡。图 4所示为来流速度为348.12,350.12及352.12时系统的响应图。由图4可以看出:在来流速度未达到分岔速度时,系统响应是稳定的,二元机翼受到扰动后能够逐渐静止于平衡点;当来流速度达到分岔速度或超过分岔速度时,系统并没有像线性系统一样颤振发散,而是颤振幅值稳定在某个特定值,出现极限环振动,如图5所示。当流速继续增大时,系统的响应始终是一个简单的极限环颤振,其振动幅值随飞行速度的增大而不断增大。因此,分岔速度成为影响非线性系统稳定的参考点,而分岔速度小于线颤振速度,当飞行速度大于分岔速度而小于线颤振速度时,系统会出现极限环振荡,使结构疲劳破坏。
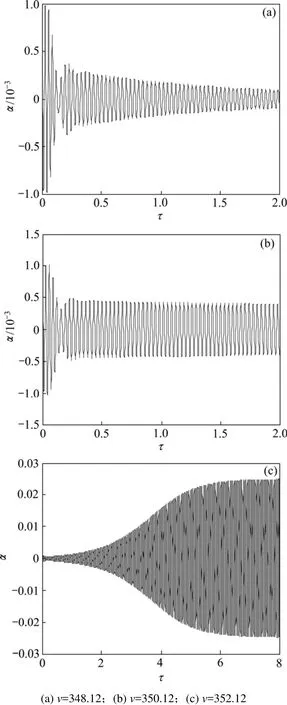
图4 俯仰振动响应曲线Fig.4 Pitching aerothermoelastic time history responses
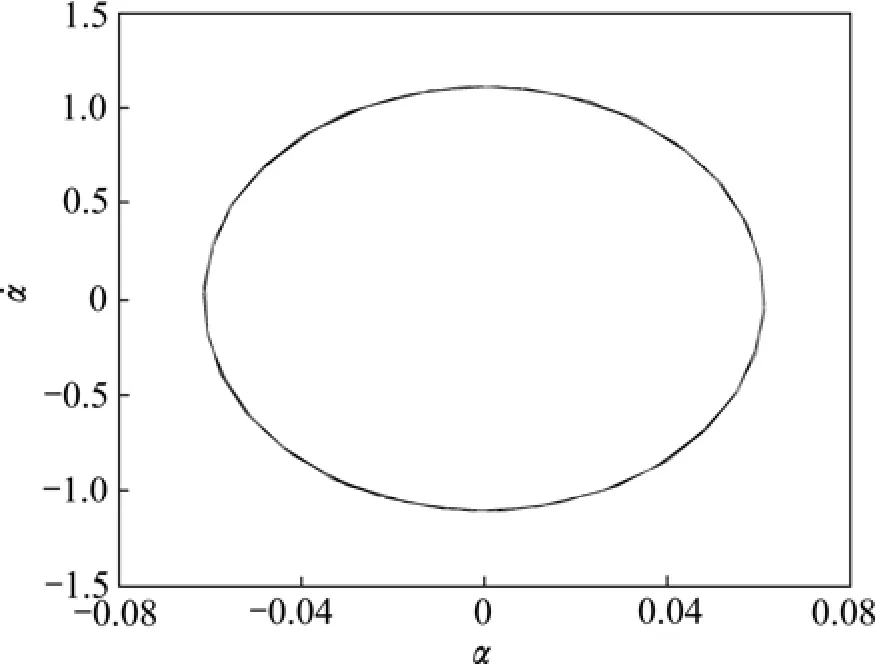
图5 俯仰运动相图Fig.5 Phase portraits of pitch motion
4 结论
(1)高超声速飞行器的颤振速度受气动热影响很大,影响飞行器的稳定性。
(2)机翼的厚度比对热颤振速度有一定的影响,随着τ的增大,热效应减小,热颤振速度变大。
(3)非线性系统的颤振问题表现为极限环振荡,但其出现极限环振荡的临界速度小于线颤振速度。
(4)在进行机翼气动弹性分析时,必须考虑迟滞非线性等因素的影响,避免出现极限环振动会使得结构疲劳受损,导致灾难性后果。而对于高超声速飞行器,其外部的放热措施至关重要,合理的放热措施可以有效提高颤振速度,增大飞行器的稳定性。
[1]Dunn P,Dugundji J.Nonlinear stall and divergence analysis of cantilevered graphite/epoxy wing[J].AIAA Journal,1992,30(1):153−162.
[2]Tang D,Dowell E H.Limit-cycle hysteresis response for a high-aspect-ratio wing model[J].Journal of Aircraft,2002,39(5):885−888.
[3]Patil M J,Hodges D H,Cesnik C E S.Nonlinear aeroelastic analysis of complete aircraft in subsonic flow[J].Journal of Aircraft,2000,37(5):753−760.
[4]Patil M J,Hodges D H,Cesnik C E S.Nonlinear aeroelasticity and flight dynamics of high-altitude long-endurance aircraft[J].Journal of Aircraft,2001,38(1):88−94.
[5]郑国勇,杨翊任.超音速流中结构非线性二元机翼的复杂响应研究[J].振动与冲击,2007,26(12):96−100.ZHENG Guo-yong,YANG Yi-ren.Complicated response of a 2-D wing structural nonlinearity in supersonic flow[J].Journal of Vibration and Shock,2007,26(12):96−100.
[6]郑国勇,鲁丽,杨翊任.大气紊流作用下超音速二元机翼的脉动响应[J].振动与冲击,2009,28(4):110−112.ZHENG Guo-yong,LU Li,YANG Yi-ren.Pulsation response of a two dimensional wing to atmosphere turbulence in supersonic flow[J].Journal of Vibration and Shock,2009,28(4):110−112.
[7]方明霞.具有迟滞非线性的高超声速机翼颤振分析[J].力学季刊,2009,30(4):626−631.FANG Ming-xia.Hypersonic airfoil flutter with hysteretic nonlinearities[J].Chinese Quarterly of Mechanics,2009,30(4):626−631.
[8]McNamara J J.Hypersonic aerothermoelastic studies for reusable launch vehicles[C]//45th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics &Materials Conference.Palm Springs,California,2004:1590.
[9]McNamara J J,Friedmann P P,Powell K G.Three-dimensional aeroelastic and aerothermoelastic behavior in hypersonic flow[C]//46th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics &Materials Confer.Austin,Texas,2005:2175.
[10]Abbas L K,CHEN Qian.Active aerithermoelastic control of hypersomic double wedge lifting surface[J].Chinese Journal of Aeronautic,2008,21(1):8−18.
[11]Abbas L K,CHEN Qian.Numerical studies of a nonlinear aeroelastic system with plunging and pitching freeplays in supersonic/hypersonic regimes[J].Aerospace Science and Technology,2007,11(4):405−418.
[12]李道春,向锦武.迟滞非线性二元机翼颤振特性分析[J].航空学报,2007,28(5):600−604.LI Dao-chun,XIANG Jin-wu.Nonlinear aeroelastic analysis of airfoil using quasi-analytical approach[J].Acta Aeronautical et Astronautica Sinica,2007,28(5):1080−1084.
[13]Thuruthimattam B J,Friedmann P P,McNamara J J.Aeroelasticity of a generic hypersonic vehicle[C]//43rd AIAA/ASME/ASCE/AHS Structures,Structural Dynamics and Materials Conference.Denver,CO,2002:1209
[14]McNamara J.Aeroelastic and aerothermoelastic behavior of two and three dimensional surfaces in hypersonic flow[D].Michigan:University of Michigan.Ann Arbor.2005:127−134.
[15]Budiansky B,Mayers J.Influence of aerodynamic heating on the effective torsional stiffness of thin wings[J].Journal of the Aeronautical Sciences,1956,23(12):1081−1093.

