分布式全局最大频繁项集挖掘算法
杨君锐,何洪德,杨莉,李海文,薛萍
(西安科技大学 计算机科学与技术学院,陕西 西安,710054)
关联规则挖掘的重点任务是频繁项目集(亦称频繁模式)挖掘。然而,由于频繁项目集挖掘具有特有的计算复杂度问题,业界提出最大频繁项目集挖掘。在单处理机上的最大频繁项目集挖掘研究方面,人们已取得许多成果[1−4]:Max-Miner算法是较早提出的典型算法[1],其基于经典的Apriori思想[5]并采用宽度优先搜索策略,实现挖掘;DMFIA算法[2]和MMFI算法[3]均基于经典的 FP-growth算法[6],不需要产生条件模式基和条件模式树,且只需扫描2遍数据库;而Mafia算法[4]采用深度优先搜索策略以及 3种剪枝方法,从而被认为是性能较好的经典算法。由于单处理机的计算能力和可利用的存储空间有限,以及网络技术与分布式数据库技术的迅速发展,使得对分布式/并行挖掘的研究成为必然。在针对分布式/并行挖掘的(全局)频繁项集算法的研究方面,研究者也已取得较多成果[7−12],如:基于 Apriori思想的 CD,DD 和 CaD[7]算法;基于FP-growth算法的MLFPT算法[8]、PFP-tree算法[9]和 FDMA 算法[10]等。这些方法通过采用FP-tree[6]存储结构,避免生成大量候选项集或条件模式树,以减小网络通信量,提高挖掘效率;还有其他算法,如FDM算法[11]、DDDM算法[12]等,它们通过减少候选项集的数目以及优化网络通信策略来降低每次迭代的通信开销,从而改善挖掘效率。与针对分布式/并行挖掘的频繁项集算法的研究相比,分布式/并行挖掘的(全局)最大频繁项集算法方面的研究较少[13−16]。DMM(Distributed Max-Miner)算法[13]采用 2阶段挖掘策略即局部挖掘与全局挖掘。在局部挖掘时,采用Max-Miner方法得到局部最大频繁项集,然后,所有节点通过交换与合并局部最大频繁项集来生成全局最大频繁项集的候选集,并将其存储在 Prefix tree中,最后通过全局挖掘,得到全局最大频繁项集;GridDMM(Grid-based distributed max-miner)算法[14]与DMM 类似,只是它是基于数据网格系统的分布式最大频繁项集挖掘算法,并且在全局最大频繁项集挖掘时采用自顶向下的搜索策略;这 2个算法均基于Apriori思想。FMGMFI(Fast mining global maximum frequent itemsets)算法[15]采用FP-Tree结构来压缩存储数据库,通过扫描数据库2遍,以及点到点通信方式和利用自底向上和自顶向下的双向搜索策略来挖掘全局最大频繁项集。但该算法存在的问题是,在挖掘时需多次扫描 FP-tree树。MGMF(Mining global maximum frequent itemsets on FP-tree)算法[16]也是基于FP-Tree的结构来压缩存储数据库,通过被约束子树MGMF[16]进行超集检测与剪枝,利用PDDM[16]播报消息的方式来广播项集,从而完成挖掘,该算法存在的问题是,它没有有效利用FP-tree结构,使得挖掘效率受到影响。本文提出一个分布式全局最大频繁项集挖掘算法(DMFI),该算法基于 FP-tree的改进频繁模式树(IFP_tree),在各站点上分别建立该存储树,并使用有序方式存储频繁项目,然后通过对各局部数据库的扫描,来挖掘出局部最大频繁项集,最后利用共享各局部数据库生成的最大频繁项集以及利用 PDDM 组通信播报消息的方式,从而挖掘出全局最大频繁项集的集合。仿真实验表明:DMFI算法具有较好的性能。
1 问题描述
1.1 相关概念
定义 1 给定一个事务数据库 D,其中事务集 T是由事务ti(i=1,2,…)组成的集合,每条事务t由标识符Tid唯一标识,则t(t∈T)所处理的项目的集合称为项集(亦称模式),记为It,T中所有事务处理的项目的集合记为 I,I={i1,i2,…,im}。设有项集 X⊂I和事务 t∈T,若X⊆It,则称事务t包含项集X。而把一个项集X中所含项目的个数称为该项集的维数或长度,记为|X|,若存在|X|=k(1≤k≤m),则称X为k_项集。
定义2 设分布式数据库D是水平划分的,且各部分的数据库逻辑同构。则在n个站点S1,S2,…,Sn上的事务数据库分别为D1,D2,…,Dn,且则称Di(1≤i≤n)为局部事务数据库,D称为全局事务数据库。|D|及|Di|分别代表D和Di中所含的事务数。
定义 3 对于项集 X,Xc和 Xci分别表示 D和 Di中包含项集X的事务数,称Xc为X在D中的全局支持数;Xci为 X在 Di中的局部支持数。若 Xs=Xc/|D|,则称Xs为X在D中的全局支持度;若Xsi=Xci/|Di|,则称Xsi(1≤i≤n)为X在Di中的局部支持度。
定义4 设给定最小支持度阈值S,对于项集X,当Xs≥S时,称X为全局频繁项集;否则,称X为非全局频繁项集。当Xsi≥S时,称X为Di的局部频繁项集;否则,称X为Di的非局部频繁项集。
定义5 对于项集X,若X为全局频繁项集,而X在D中的任何超集都为非全局频繁项集,则称X为全局最大频繁项集;所有X的集合称为全局最大频繁项集的集合,记为MFS(Maximal frequent sets)。若X为Di(1≤i≤n)的局部频繁项集,而X在Di中的任何超集都为非全局频繁项集,则称X为局部最大频繁项集;所有 X的集合称为局部最大频繁项集的集合,记为MFSi。
定义 6 对所有频繁 1_项集(以下简称为频繁项目),按其支持数降序的排列,称为频繁项目的列表L1。对L1中的频繁项目依次进行编号(从“1”开始)后的列表,称为频繁项目的序列表L1′。
由上述定义易得下列性质和定理。
性质1 任一最大频繁项集均由L1或L1′中的频繁项目组成,且该最大频繁项集的所有非空子集都是频繁项集。
性质2[10]若项集X为全局频繁项集,则至少存在一站点Si(1≤i≤n),使得X及X的所有非空子集在站点Si上为局部频繁项集。
定理1[15]如果项集X是全局最大频繁项集,则必存在一站点Si(1≤i≤n),使得X为其上某一局部最大频繁项集的子集。
由定理1可得下列推论。
推论 若项集X不是任一站点Si(1≤i≤n)上的局部最大频繁项集的子集,则X一定不是全局最大频繁项集。
定理2 设项集Y为某站点上的局部最大频繁项集,X⊆Y且为全局频繁项集。若对任意站点上的任意局部最大频繁项集Y′,不存在全局频繁项集Z⊆Y′使得X⊆Z,则X是全局最大频繁项集。
证明:(反证法)由推论1可知:全局最大频繁项集可通过局部最大频繁项集的子集得到。若X不是全局最大频繁项集,因为X为全局频繁项集,则设X⊆Z且Z为全局最大频繁项集,由定理1知,一定存在某个站点Si使得Z⊆Y′且Y′为局部最大频繁项集,这与已知条件矛盾。从而定理得证。
1.2 IFP-tree
针对最大频繁项集的特点,提出基于FP-tree[6]的改进数据存储结构IFP-tree,用于数据信息的存储。
IFP-tree为满足以下3个条件的树型结构:
(1)有1个标记为“root”的根节点。
(2)IFP-tree的节点由 6个域组成:节点序号(node_no)为该节点所代表的频繁项目在L1′中的序号;节点计数(node_count)记录从根节点到该节点的路径上所代表的频繁项目在数据库中出现的次数;节点的子链接(child_link)是指向该节点的第 1个子节点的指针;节点的兄弟链接(brother_link)是指向该节点的兄弟节点的指针;节点的父链接(parent_link)是指向该节点的父节点的指针;同名节点链(node_link)是指向IFP-tree中同名节点的指针。
(3)IFP-tree包含1个项目头表Htable,而该表的每个表项包含 2个域:item_no(项目序号,其作用与node_no的相同);item_head(项目链头)为指向IFP-tree中具有相同的item_no的首节点指针。
IFP-tree的构造算法如下(各站点 Si(1≤i≤n)同步):
(1)扫描各局部事务数据库 Di,得到各项目的局部支持数。然后,对所有的局部支持数进行规约求和,继而得到各项目的全局支持数。最后得到全局频繁项目,并据此得到L1和L1′。
(2)创建IFP-tree的根节点R,标记为“root”,且使R.child_link=Null,R.brother_link=Null,R.parent_link=Null。
(3)按L1的次序排列事务t中的频繁项目,忽略t中非频繁项目,然后,按L1′对其进行对应编号代替,得到 t′。
(4)假定排序后t′的结果为[n|N],其中n是第一个频繁项目的编号,N是剩余频繁项目的编号列表。然后,按照类似FP-Tree的生成过程得到初始树IFP-tree。
(5)在初始树IFP-tree中,对任意一个节点A,判断A的孩子子树和A的兄弟子树中是否有node_no相同的节点,若有,则进行合并,即先将 2节点的node_count相加,作为 A的兄弟子树中此节点新的node_count,A的孩子子树保持不变;然后将层次计数器增1,比较下一层对应节点的node_no,重复上述过程,直到出现node_no不相同时停止。若node_no值不相同,则将A的孩子子树中的节点插入到A的兄弟子树中(详细的合并过程见文献[17])。
(6)将Htable中item_no对应的item_head链接到节点序号为item-no的首节点。
设全局事务数据库 D如表 1所示(表中 Frequent items栏给出的是:该D在最小支持度阈值S=0.5时的频繁项集;item_no栏为频繁项集对应的编号),有 2个站点S1和S2可用,D1存放D中的前4条事务,D2存放 D中的后 4条事务,则 D1对应的频繁模式树IFP-tree的构造结果如图1所示。其中:圆圈中冒号前的数字为节点的 node_no,冒号后的数字为节点的node_count。
根据IFP-tree的结构和构造过程易得下列性质和定理。设给定事务数据库D,D对应的频繁模式树为IFP-tree,最小支持度阈值 S,即最小支持数阈值 ξ(ξ=S×|D|)。
性质3 事务数据库D中所含的任一频繁项集都被记录在IFP-tree的某条路径上。
性质4 在IFP-tree中,节点的node_count值从上到下降序排列;节点的node_no值从左到右升序排列。
由IFP-tree结构易得下列定理3。
定理3 在IFP-tree中,若某节点计数不小于最小支持数阈值 ξ,则以该节点和其前缀路径中的节点组成的项集必为频繁项集。

表1 全局事务数据库Table 1 Global Business database

图1 D1对应的IFP-treeFig.1 IFP-tree of D1
定理4 在IFP-tree中,若某节点N的node_count≥ξ,而N的子节点的node_count<ξ,则N的所有子孙节点的node_count<ξ。这样,从根节点R到N的路径上的节点就是1个最大频繁项集或最大频繁项集的候选集。
证明:若某节点N的子节点的node_count<ξ,由性质4可知,N的子节点以下的所有节点的node_count<ξ,即 N的下层子树没有频繁节点,故从根节点 R到N的路径就构成了D的1个最大频繁项集或最大频繁项集的候选集。证毕。
2 分布式全局最大频繁项集挖掘算法DMFI
假设有n台基于共享体系结构的计算机,组成n个站点 Si(1≤i≤n),事务数据库 D被均分成 n份 Di存于各站点。站点 Si上的 Di对应的频繁模式树记为IFP-treei,根节点为rooti,其对应的局部最大频繁项集的集合和候选集合分别记为MFSi和 CFSi。而 MFCS为MFSi的并集。
2.1 DMFI算法的基本策略
DMFI算法的基本策略是:(1)对各站点Si,分别创建完全独立、互不影响的 IFP-treei。另外,为提高挖掘效率,IFP-treei采用合并策略[17],即把具有相同前缀的子树合并在一起,从而不需要构造条件模式树;(2)整个挖掘分为局部挖掘与全局挖掘2个阶段;(3)根据定理3和4,在局部挖掘中,采用深度优先搜索和宽度优先搜索相结合的方式,即深度优先是根据child_link链接由根节点不断向子节点的搜索,宽度优先是根据brother_link链接而完成的横向搜索,从而先得到CFSi,继而得到MFSi和MFCS;(4)在全局挖掘中,采用共享体系结构,共享各站点生成的局部最大频繁项集MFCS,在各站点处理器同步的情况下,依次对MFCS中维数最大的项集利用PDDM组通信播报消息的方式来广播以及挖掘,直至MFCS为空,最终得到全局最大频繁项集的集合。
2.2 DMFI算法描述
DMFI算法由局部最大频繁项集的挖掘 LMFI( )与全局最大频繁项集的挖掘GMFI( )2部分组成。下面分别描述。
Procedure LMFI( )
输入:局部事务数据库 Di(1≤i≤n)对应的IFP-treei;最小支持度阈值S。
输出:局部最大频繁项集的集合MFSi。
1.MFSi=CFSi=NULL
2.将非根节点N设为当前节点;
3.while(当前节点!= NULL)
4.{ if(当前节点的计数 ≥ S×|Di|)
5.then { CFSi= CFSi∪从根节点到当前节点的路径所组成的项集;
6.将N的子节点设为当前节点;}
7.else {将N的子节点的兄弟节点设置为当前节点;}
8.}
9.将N的兄弟节点设置为当前节点;
10.GOTO 3;
11.从CFSi中检出局部最大频繁项集,并送入MFSi;
12.return MFSi;
Procedure GMFI( )
输入:MFSi(1≤i≤n);最小支持数阈值ξ。
输出:全局最大频繁项集的集合MFS。
1.MFS=Null;MFCS = MFS1∪MFS2∪…∪MFSn;
2.while MFCS ≠ ∅ do
3.{ 同步各处理器;
4.从MFCS中无放回的取出维数最大的项集X,并设 X∈MFSi(i=1,…,n);
5.if(X的计数X.ci≥ξ )
6.then { MFS = MFS∪{X};break;}
7.else { 站点Si以组方式将X的信息发送到其他站点 Sj(1≤j≤n 且 j≠i);
8.各站点 Sj将各自的局部支持数发送到站点Si;
9.站点 Si计算全局支持数,即 X.c=
10.if(X.c≥ξ)then { MFS = MFS∪{X};break;}
11.else 将|X|_项集 X 的所有(|X|-1)维项集(即 X的所有(|X|-1)维子项集)并入MFCS;} }
12.return MFS;
3 算法测试与性能分析
为验证算法DMFI的性能,对算法进行实验测试。实验环境是在10Mb的局域网中,用数台PC机(具体台数随测试内容不同而不同)构成分布式站点,各台PC机配置均为:操作系统为 Windows XP,CPU为PIV400,内存为1 GB。实验程序均采用VC++6.0实现。实验中选用的数据集分别是由 http://www.ics.uci.edu/~mlearn/MLRepository.html上提供的蘑菇数据库mushroom(该数据库含有8 124条记录,记录蘑菇的 23种属性)和由 IBM Almaden实验室(http://www.almaden.ibm.com/cs/projects/iis)提供的 T|T|I|I|D|D|合成数据库(其中|T|表示数据集中事务的平均长度,|I|表示潜在频繁项集的平均长度,|D|表示数据库中总的事务数目)中的 T40I10D100k和 T40I10D1000k。测试从以下几方面进行。
3.1 执行效率的对比测试与分析
由于目前针对基于分布式的最大频繁项集的挖掘研究成果较少,在进行研究与分析后,选择性能相对较好的FMGMFI算法[15]和MGMF算法[16]作为实验中的比较测试对象。
测试方法(3.2节同样也采用此方法)是:先由3台PC机构成分布式站点,然后将选用的交易数据库 D均分到3个站点,且使各站点的记录数相等,最后,分别用FMGMFI,MGMF和DMFI来挖掘全局最大频繁项集。
当最小支持度阈值S分别取10%,20%,30%,40%,50%,60%,70%,80%和90%,而当选用的数据库分别为mushroom,T40I10D100k和T40I10D1000k时,3个算法的执行结果如图2~4所示。另外,在不同情况下执行时,经比较3个算法挖掘的结果也完全一样。从测试结果可看出,DMFI算法的性能明显优于FMGMFI和MGMF算法。
3.2 通信次数测试与分析
当最小支持度阈值 S分别从 10%到 90%时,FMGMFI,MGMF和DMFI算法分别在T40I10D100k上挖掘全局最大频繁项集时需要的通信次数结果如图 5所示。
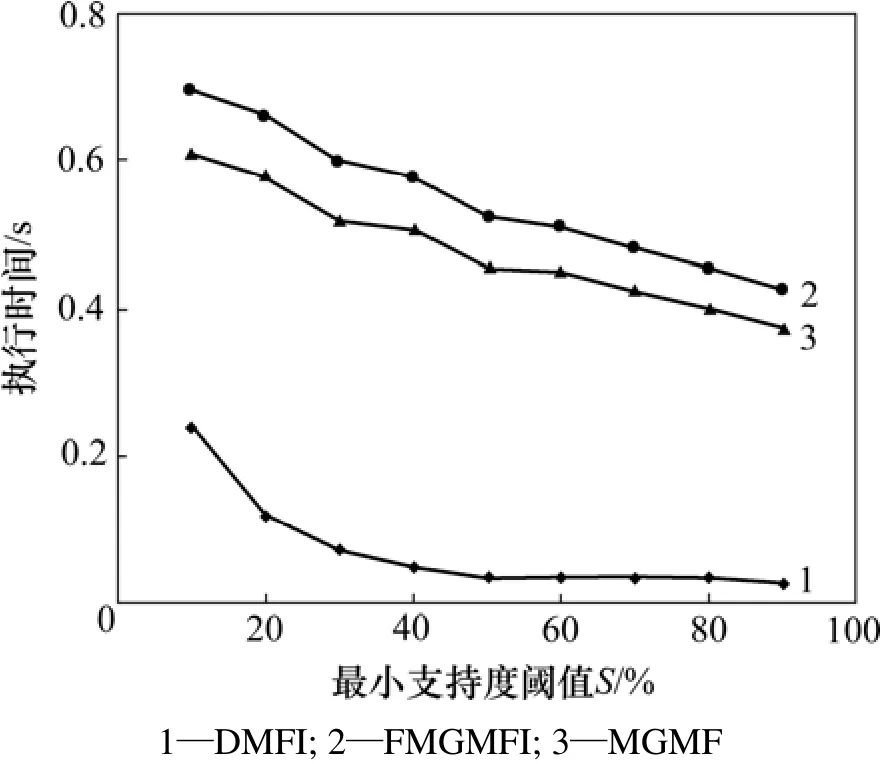
图2 在mushroom数据库上的对比Fig.2 Experimental results on mushroom database

图3 在T40I10D100k数据集上的对比Fig.3 Experimental results on T40I10D100k
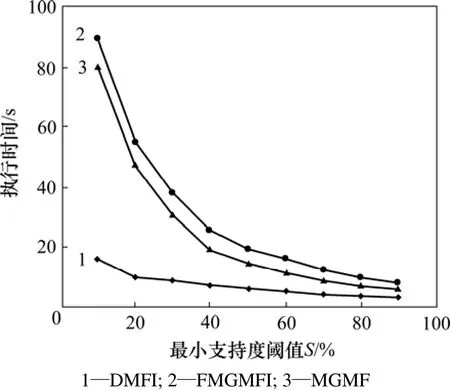
图4 在T40I10D1000k数据集上的对比Fig.4 Experimental results on T40I10D1000k
从图5可见:DMFI算法需要的通信次数最少。已知在分布式挖掘中,通信次数的多少将影响算法的执行效率,所以,此结果也说明DMFI算法的高效性。

图5 在T40I10D100k上网络通信次数的对比Fig.5 Comparison of communication on T40I10D100k
3.3 可扩展性测试与分析
可扩展性是指问题规模增大时,算法性能不会降低。对分布式关联规则挖掘算法,问题规模增大时有以下 2种情况:(1)参与挖掘的处理器数目增加;(2)数据库规模增大。下面分别从这 2个方面进行DMFI算法的可扩展性测试。
3.3.1 参与挖掘的处理器数目增加
对于分布式算法,处理器个数直接影响算法的执行效率。这里通过加速比反映处理器个数对算法性能的影响。分布式算法的加速比定义[18]为:Sp=T1/Tp(其中,T1指单个站点上算法的运行时间;Tp指p个站点上分布式算法的运行时间)。
最小支持度阈值取S=15%,处理器台数依次增加,分别选用2,3,4,5,6和7台,测试选用T40I10D100k,并将数据依次均分到不同站点。测试结果如表2所示。
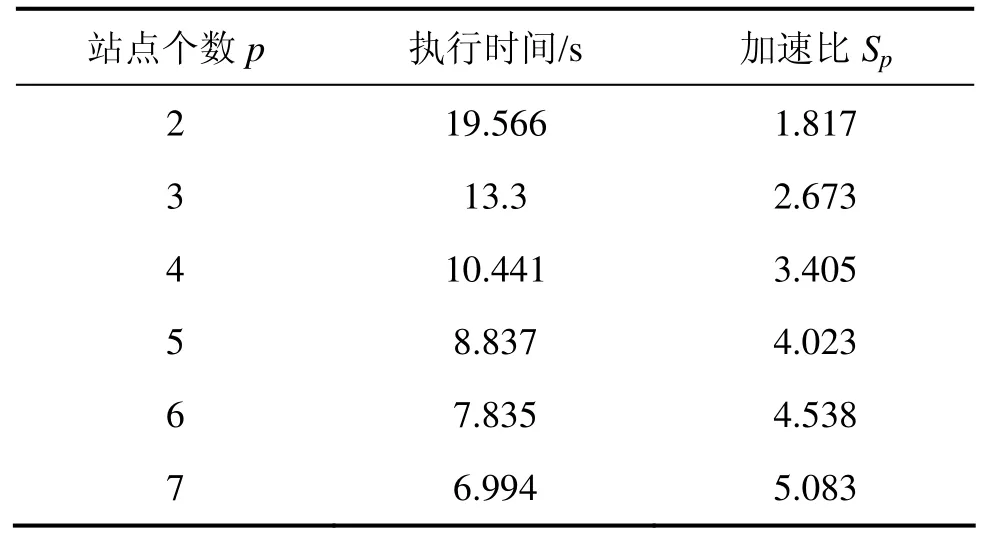
表2 在T40I10D100k上的扩展性测试结果Table 2 Results of scalability tests on T40I10D100k
从表2可知:当处理器个数为2时,算法的执行时间最大,执行加速比最小。之后随着处理器个数 p的不断增加,算法执行时间依次减少,而加速比依次提高,也就是说执行效率不断提高。
3.3.2 数据库规模增大
分布式站点由 3台 PC机构成。测试选用T40I10D100k,最小支持度阈值S取15%。测试方法是:先取数据集中的前10×103条记录(均分到3站点)进行挖掘,随后数据规模以10×103条记录递增后(同样是均分到 3站点)再挖掘,直到 100×103条为止。测试结果如图6所示。从图6可见:随着数据集规模的增长,算法执行时间基本呈线性稳步增长。
从以上测试结果,说明DMFI算法具有较好的可扩展性。
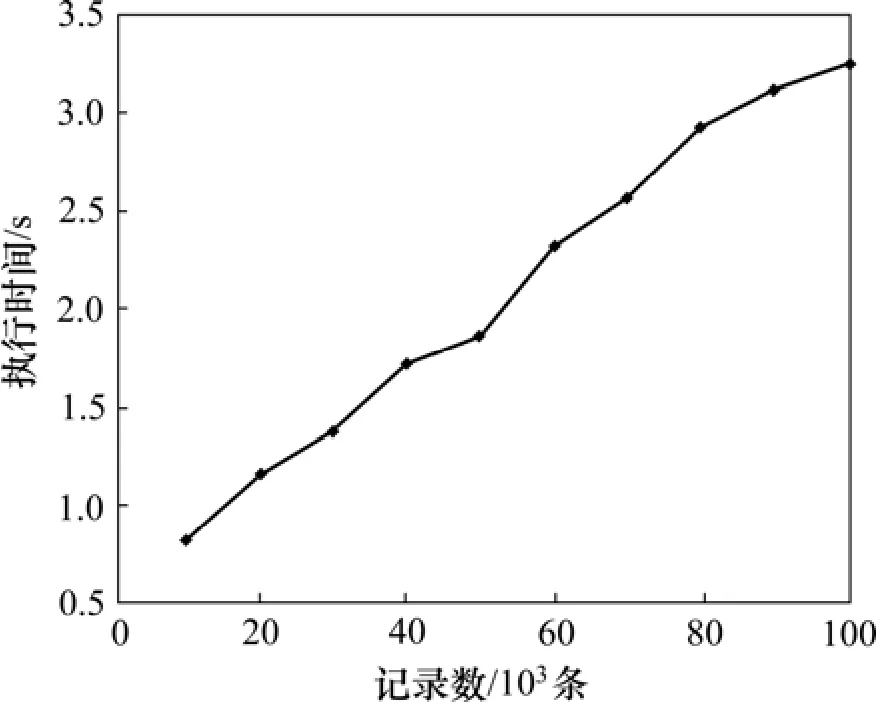
图6 T40I10D100k数据集上的扩展性测试Fig.6 Scalability tests on T40I10D100k
4 结论
(1)根据分布式挖掘的特点,提出全局最大频繁项集挖掘算法 DMFI。该算法采用文中提出的改进频繁模式树IFP-tree来存储数据信息,并采用数字有序方式来表示项目信息,从而只需对事务数据库扫描 2次,同时算法采用组通信播报消息的思想来实现站点间的通信,最终得到全局最大频繁项集。
(2)DMFI具有较高的效率。
[1]Bayardo R J.Efficiently mining long patterns from databases[C]//Proceedings of the ACM SIGMOD Int’l Conference on Management of Data.New York:ACM Press,1998:85−93.
[2]宋余庆,朱玉全,孙志挥.基于FP-Tree的最大频繁项目集挖掘及更新算法[J].软件学报,2003,14(9):1586−1592.SONG Yu-qing,ZHU Yu-quan,SUN Zhi-hui.An Algorithm and Its Updating Algorithm Based on FP-Tree for Mining Maximum Frequent Itemsets[J].Journal of Software,2003,14(9):1586−1592.
[3]SG J,Chen C.MMFI:An effective algorithm for mining maximal frequent itemsets[C]//Proceedings of the IEEE International Symposium on Information Processing,IEEE CS Press,2008:26−30.
[4]Burdick D,Calimlim M,Gehrke J.Mafia:A maximal frequent itemset algorithm for transactional Database[C]//the 17th International Conference on Data Engineering.Heidelberg:IEEE Computer Society Press,2001:443−452.
[5]Agrawal R,Srikant R.Fast algorithms for mining association rules[C]//Proceedings of the 20th International Conference on Very Large Data Bases.Santigo,San Francisco:Morgan Kaufmann Publishers Inc,1994:487−499.
[6]Han J,Jian P,Yiwen Y.Mining frequent patterns without candidate generation[C]//Proceedings of 2000 ACM SIGMOD Int’l Conference on Management of Data.Dallas:ACM Press,2000:1−12.
[7]Agrawal R,Sharfer J.Parallel Mining of Association Rules[J].IEEE Transactions on Knowledge and Data Engineering,1996,8(6):962−969.
[8]Zaiane O R,EI-Hajj M,Lu P.Fast parallel association rule mining without candidacy generation[C]//Proceedings of the 2001 IEEE International Conference on Data Mining.Washington:IEEE Computer Society Press,2001:665−668.
[9]Javed A,Khokhar A.Frequent pattern mining on message passing multiprocessor systems[J].Distributed and Parallel Databases,2004,16(3):321−334.
[10]宋宝莉,覃征.分布式全局频繁项目集的快速挖掘方法[J].西安交通大学学报,2006,40(8):923−927.SONG Bao-li,QIN Zheng.Fast mining algorithm for distributed global frequent itemsets[J].Journal of Xi’an Jiaotong University,2006,40(8):923−927.
[11]Cheung D W,Han J W,Ng V T.A fast distributed algorithm for mining association rules[C]//Proceedings of IEEE the 4th International Conference Parallel and Distributed Information Systems.Heidelberg:IEEE Computer Society Press,1996:31−44.
[12]Schuster A,Wolff R.Communication efficient distributed mining of association rules[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data.New York:ACM Press,2001:473−484.
[13]Chung S M,Luo C.Distributed mining of maximal frequent itemsets from databases on a cluster of workstations[C]//2004 IEEE International Symposium on Cluster Computing and the Grid.Washington:IEEE Computer Society Press,2004:499−507.
[14]Luo C,Pereira A L,Chung S M.Distributed mining of maximal frequent itemsets on a data grid system[J].The Journal of Supercomputing,2006,37(1):71−90.
[15]陆介平,杨明,孙志挥,等.快速挖掘全局最大频繁项目集[J].软件学报,2005,16(4):553−560.LU Jie-ping,YANG Ming,SUN Zhi-hui,et al.Fast mining of global maximum frequent itemsets[J].Journal of Software,2005,16(4):553−560.
[16]王黎明,赵辉.基于 FP树的全局最大频繁项集挖掘算法[J].计算机研究与发展,2007,44(3):445−451.WANG Li-ming,ZHAO Hui.Algorithm of mining global maximum frequent itemsets based on FP-tree[J].Journal of Computer Research and Development,2007,44(3):445−451.
[17]YANG Jun-rui,GUO Yun-kai.Fast mining maximal frequent itemsets based on sorted FP-tree[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing:Chongqing University,2008:5391−5395.
[18]孙世新,卢光辉,张艳,等.并行算法及其应用[M].北京:机械工业出版社,2005:32−45.SUN Shi-xin,LU Guang-hui,ZHANG Yan,et al.Parallel algorithm and its application[M].Beijing:Machinery Industry Press,2005:32−45.

