铁路框构顶进工程接触网支架改移方案设计

王雨权

(铁道第三勘察设计院集团有限公司，天津 300142)

1 工程概况

天津市规划公路与津山铁路相交，为了使公路工程顺利进行，必须在相交处实施框构顶进工程。顶进框构结构宽64m，框构顶部铁路线路状况复杂，共有12股道。

在该处，既有铁路为电气化铁路，由于框构宽度较大，在施工的时候，原有的接触网支柱需要进行改移，改移方案如图1所示，即将原073、130、077、138号接触网分别外移到编号为 X001、X003、X001、X004、X006的新位置。在X001和X004之间以及X003和X006之间分别假设两个钢梁，然后在两钢梁之间拉接触网线。以代替原075号和132号、134号之间的接触网。

所改造的接触网对两侧钢桥分别作用有竖直向下的力4.1 kN，水平垂直于线路方向的力109 kN。所设计钢梁的梁底要高于轨面高度6.4m，钢梁的梁顶高于轨面高度7.56m。

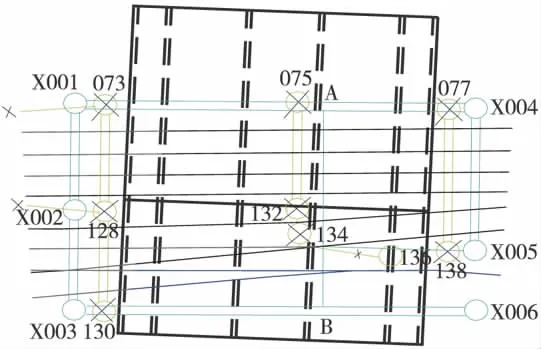
图1 接触网改造示意

2 钢梁设计方案

综合上述工程状况及接触网改造的要求，设计的钢梁及钢墩方案的立面如图2所示，横截面采用2m×2m，材料采用Q235角钢，其中，上下弦及钢墩的主受力杆件采用双角钢，尺寸为200 mm×200 mm×24 mm，腹杆采用160 mm×160 mm×14 mm的单角钢。计算时考虑温度应力的作用，为了控制温度应力，钢梁与桥墩之间用支座联结，跨度76m。计算采用midas有限元计算软件进行计算，根据拟定的设计方案建立的有限元模型如图3所示。

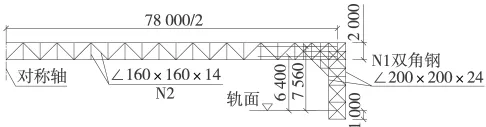
图2 钢梁立面示意(单位:mm)

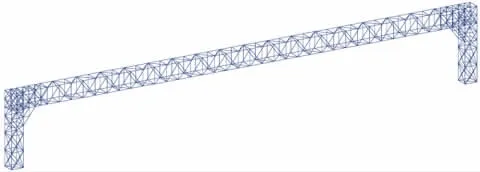
图3 钢梁有限元计算模型

3 计算荷载分析

利用有限元模型分析计算时，分别考虑如下的荷载。

①自重。

②接触网作用水平拉力:103+6=109 kN。

③接触网作用竖向拉力:4.1 kN。

④钢梁所受横向水平风力。

桥梁上的的风荷载强度计算公式为

根据《铁路桥涵设计基本规范》(TB10002.1—2005)的附录 D可得，天津地区的基本风压 W0=600 Pa，k1为风载体形系数，根据规范取1.3;k2为风压高度变化系数，本处钢梁离地面的高度≤20m，根据规范取1.0;k3为地形、地理条件系数，本工程所在地属于一般平坦空旷地区，根据规范取1.0。

根据规范规定，钢桁梁及钢塔架横向风力的受风面积应按桥跨结构理论:轮廓面积乘以0.4计算。按照上述规定计算得到的总荷载均匀分布到每一个桁架节点上，横梁部分共110个节点，所以每一个节点的横向风力为钢梁墩按照高7m计算(考虑最底部的1m在轨面以下)，每一个墩的节点数为19个，所以每一个节点的横向风力为

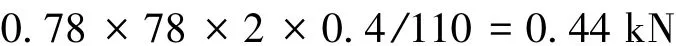
⑤钢梁所受纵向水平风力

可得纵向力为

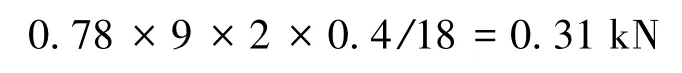
⑥温度力

规范规定，桥梁结构需计算均匀温差和日照温差引起的变形和应力，考虑到该框构将在冬季施工，计算时取单元升温50℃，降温35℃分别计算，并且要控制钢梁的合龙温度在10℃～20℃之间进行。

⑦主力工况

计算主力时，分别将自重、接触网水平力和接触网竖向力作为主力的构成部分。

⑧主力+风力工况

分别计算主力和横向风及主力与纵向风的组合，允许应力提高系数为1.2。

⑨主力+风力+温度应力工况

在主力+风力工况的基础上，加上温度荷载(分升温50℃和降温35℃两种情况考虑)。

4 强度验算

在钢材材料采用Q235qD的情况下，主桁单元采用等边双角钢，尺寸为200 mm×200 mm×24 mm，綴条采用等边角钢，尺寸为160 mm×160 mm×14 mm。计算模型采用桁架单元，故计算单元的应力允许值应该采用规范中的轴向应力允许值。根据规范，角钢厚度小于16 mm时，允许应力不需要折减，故采用135 MPa，大于16 mm时，需要折减，且折减方法按照屈服点的比例进行计算。由《铁路桥梁钢结构设计规范》(TB10002.2—2005)的附录 A可知，对于 Q235qD钢材，大于16 mm的屈服点为225 MPa，小于16 mm的钢材的屈服点为235 MPa。所以对于200 mm×200 mm×24 mm的角钢的允许值为

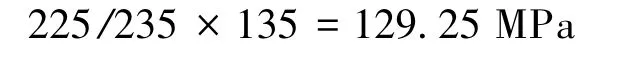
160 mm×160 mm×14 mm角钢的允许值为135 MPa。

表1是结构在几种工况下，钢梁的上下弦杆的应力计算值，表2为结构在几种工况下腹杆的应力计算值(表中应力的单位为MPa)。

表1 上下弦杆应力计算值 MPa

表2 腹杆应力计算值 MPa

从计算结果可以看出，钢梁在各种荷载作用下满足强度要求，并且控制单元在钢梁的跨中位置。对于主力工况作用下，拉应力最大值为120.26 MPa，压应力的最大值为93.57 MPa，相对于其他几种荷载工况，比较接近应力允许值。对于腹杆来说，在各种工况下的应力值均有一定的安全度，所以强度指标不控制腹杆。

下面是几种应力较大工况荷载作用下的计算结果，如图4至图6所示，图中所示的极值已经提取到表1、表2中。

图4 主力工况下的应力结果

图5 主力+横向风力+升温工况下的应力结果

图6 主力+横向风力+降温工况下的应力结果

5 挠度计算

接触网的悬挂架和电力线有高度要求，而钢梁在各个方向的挠度值，势必影响到接触网电力线的最终高程。为了给接触网设计高度提供依据，需要分别计算各种荷载工况下，钢梁在悬挂架及电力线位置的挠度值。

表3为根据计算结果提取的钢梁在各种荷载工况下的挠度值。

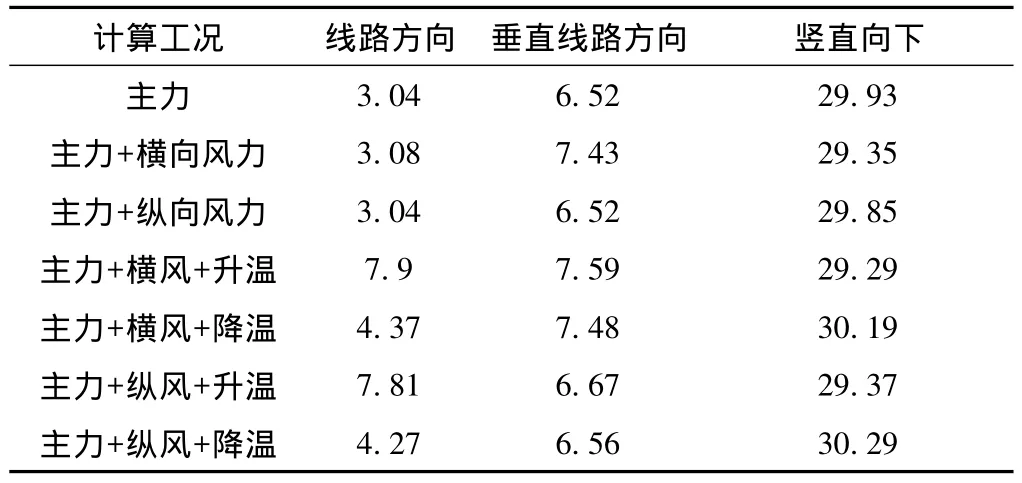
表3 挠度计算值

从表3中可以看出，在各种荷载工况下，钢梁在各个方向的挠度值比较大，设计时需要据此设置预拱度，并且接触网计算最终高程时，需要考虑该挠度的影响。

6 稳定性验算

根据规范规定，钢结构需要验算各种荷载工况下的稳定性。稳定性验算的对象是杆件受压较大的部位，并且需要对弦杆和腹杆分别进行验证计算，下面分别对不同杆件进行稳定性验算。

6.1 上下弦单元的稳定性验算

钢梁上下弦杆的单元为双角钢结构，角钢之间背靠背焊接，如图7所示。

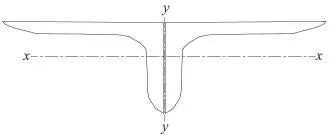
图7 弦杆双角钢截面示意

从表1可以看出，对稳定起控制性的工况为:主力+横向(纵向)风力+温度力(升温)，此时杆件的最大压应力为123.6 MPa，现分别按绕x轴和y轴进行验算。

(1)绕x轴的稳定性

根据钢梁的结构特点及《铁路桥梁钢结构设计规范》(TB10002.2—2005)的表5.1.1的规定，该杆件的计算长度为2m=200 cm。弦杆的截面示意图如图5所示，根据角钢型号，可以查型钢表得到该截面的面积为181.32 cm2;

绕x轴(x轴和y轴均为双角钢的惯性轴)的惯性矩为Ix=2×3 338=6 676 cm4;

可得该截面绕x轴的回转半径为

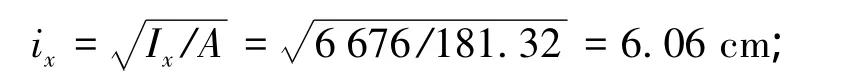
可得长细比λx=200/6.06=33。

该值小于《铁路桥梁钢结构设计规范》(TB10002.2—2005)的表5.2.1的规定的允许长细比100。

根据规范表3.2.6得:稳定性折减系数为0.878。

123.6≤0.878×129.25×1.2=136.1 MPa

绕x轴满足稳定性要求。

(2)绕y轴的稳定性

下面按照类似的方法求解绕y轴的稳定性，计算过程如下

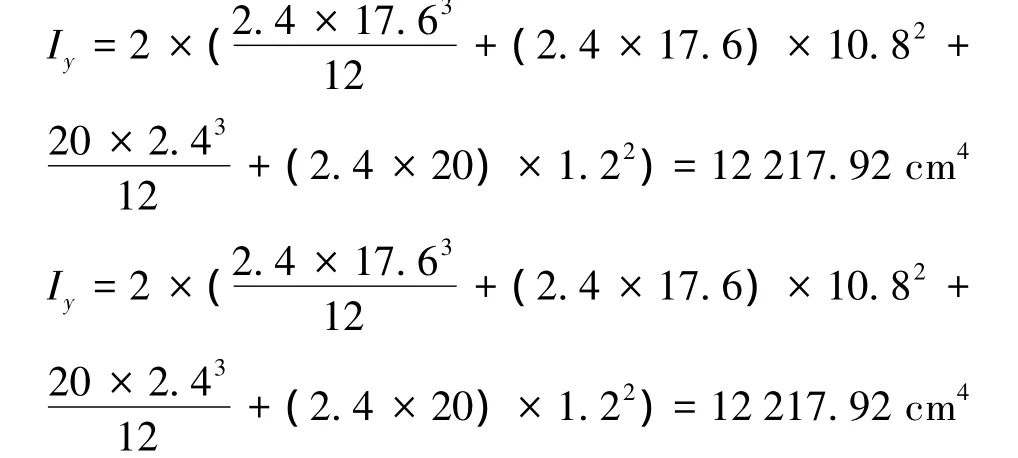
面积A=2×90.66=181.32 cm2;

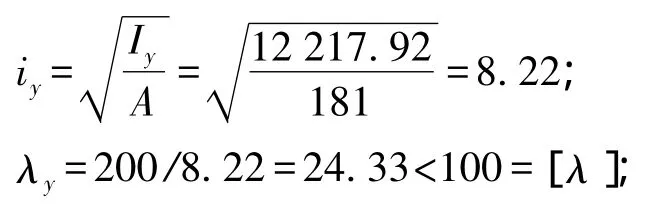
查《铁路桥梁钢结构设计规范》表3.2.6可得:φ1=0.9;

123.6≤0.9×129.25×1.2=139.6 MPa

绕y轴满足稳定性要求。

6.2 腹板单元的稳定性验算

腹杆单元为标准角钢，其几何参数可以查表得到，角钢尺寸为160 mm×160 mm×14 mm的最小回转半径为iy=3.16。所以可得长细比为

查《铁路桥梁钢结构设计规范》可得:φ1=0.598。

主力情况下:

φ1×135=0.598×135=80.73＞47.8;

满足要求。在主力+附加力情况下:

φ1×135×1.2=0.598×135×1.2=96.9＞52.4;

满足要求。

7 结束语

根据工程实际状况和接触网设置要求，经过反复优化设计，设计出的钢梁结构经过强度验算、挠度验算和稳定性验算，结果表明，该钢梁用于本工程接触网的改移满足要求。

［1］TB10002.1—2005 铁路桥涵设计基本规范［S］

［2］TB10002.2—2005 铁路桥梁钢结构设计规范［S］

［3］李富文，伏魁先，刘学信．钢桥［M］．北京:中国铁道出版社，2002

［4］铁道专业设计院．钢桥［M］．北京:中国铁道出版社，2003