基于EGM2008模型的GPS高程转换方法研究
许双安
(中铁第一勘察设计院集团有限公司,陕西西安 710043)
传统的几何水准测量方法是测定正常高的主要方法,这种方法虽然精度高,但是费时费力,作业效率低,不能很好地满足当今信息化时代的高效率、高精度、经济方便的要求,在西部海拔较高的地区及荒漠无人区,水准施测更是存在诸多困难。近年来,GPS技术以其高精度、全天候、成本低、效率高的优点被广泛应用于测绘的各个方面。在诸多应用中,GPS测得的平面精度已经足于满足应用需要;同时,GPS技术也能较容易并以相当高的精度获得测站的大地高,但这种GPS直接测得的高程是相对于椭球面的大地高,只具有几何意义,与我国采用的正常高系统不一致。如图1所示,大地高与正常高的关系为:H=h正常-ξ,式中H为大地高,h正常为正常高,ξ为高程异常。因此,除了个别特殊用途外,在实际工程应用中将GPS大地高转换为正常高是非常必要的。
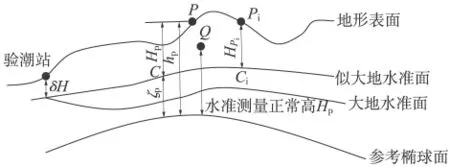
图1 高程系统关系
目前,可以通过多种方法得到似大地水准面高或高程异常数据,常用的方法有:①高程等值线图法,这种方法和从等高线图上内插出水准高程的方法相似,其精度受高程异常图或似大地水准面高图的精度和图上内插精度的影响,精度较差,是一种极其粗略的方法。②地球重力场模型法,它是利用全球重力场模型计算大地水准面高或高程异常。③数学拟合法,利用高程异常具有一定的几何相关性原理,用测区布设的一定GPS/水准点,利用数值计算的方法拟合高程异常。高程异常推估方法有平面拟合、曲面拟合、多面函数拟合等,精度依赖于建模时GPS水准点的密度、分布及高程异常变化幅度。④区域似大地水准面精化法,是在国家空间基准框架的基础上,建立集平面、高程、重力场信息于一体的综合性基础控制网,在此基础上,综合利用GPS水准、重力等资料获得厘米级的区域似大地水准面,达到实现通过GPS测量来代替低等级水准测量的目的[1],但由于重力测量资料严重不足以及实施重力测量的难度,精度也受到限制。
上述方法方法也存在局限性,方法②和④仅仅适用于有足够重力场资料和精密似大地水准面模型的区域,方法③仅适用于能联测足够密度GPS水准点且势起伏较小的局部区域。对于西部海拔起伏较大的山区火荒漠无人区,缺乏高精度重力场和似大地水准面模型,GPS水准点分布较少,上述GPS高程转换方法不再适用。
针对没有进行似大地水准面模型精化或无法联测GPS/水准点的局部区域,本文尝试利用已有的高分辨高精度地球重力场模型EGM2008,直接进行GPS高程转换。
1 地球重力场模型EGM2008
地球重力场模型是用以描述和表示地球重力场的一类基本参数的集合,包括位系数、大地水准面高、垂线偏差、重力梯度等,是对地球重力场的逼近或拟合。地球重力场模型EGM2008是由美国国家地理空间情报局(NGA)在2008年4月发布的最新一代全球重力场模型。EGM2008的研制是由美国国家宇航局哥达飞行中心(NASA/GSFC)、美国国家影像制图局(N IMA)和美国国防部(DOD)以及俄亥俄州大学合作完成。研究和总结以往地球重力场模型的经验和理论基础上,以PGM2007B(PGM2007A的变种模型)为参考模型,利用GRACE卫星采集的重力数据、卫星跟踪数据、全球5'×5'的地面重力异常数据和TOPEX卫星测高数据,以及现势性好、分辨率高的地形数据,结合精度高、覆盖面广的地面重力数据,采用最先进的建模技术与算法,完成的最新一代全球重力场模型[2][3]。
EGM2008重力场模型的阶次完全至2159(另外球谐系数的阶扩展至2190,次为2159),相当于模型的空间分辨率约9 km,是目前分辨率和精度最高的重力场模型。EGM2008模型提供的最终成果包括[4]:①2190阶次的全球重力场模型;②全球5'×5'网格重力异常;③全球 5'×5'、2.5'×2.5'网格大地水准面;④全球5'×5'网格垂线偏差(ξ,η)。国内学者研究表明:EGM2008模型高程异常在我国大陆的总体精度为20 cm,华东华中地区12 cm,华北地区达到9 cm,西部地区为 24 cm[5]。
上述成果可从国际上多个组织如NGA、GFZ官方网站上免费下载,本文使用的是NGA提供的1'×1'网格大地水准面。
2 基于EGM2008的高程转换方法
利用EGM2008模型进行GPS高程转换,可分为以下步骤:①获取待测点高精度大地高;②利用EGM2008模型成果计算出待测点高程异常值;③高程转换及残差处理。
2.1 获取高精度大地高
根据NGA提供的报告显示,EGM2008提供的1'×1'网格大地水准面是基于WGS-84,在成果使用时应保持框架定义一致。可以采用精密单点定位技术或静态相对定位技术获得基于WGS-84参考椭球的大地高[6,7]。
2.2 利用重力场模型求解高程异常
根据地球重力场模型,地面点 P(ρ,θ,λ)的重力扰动位
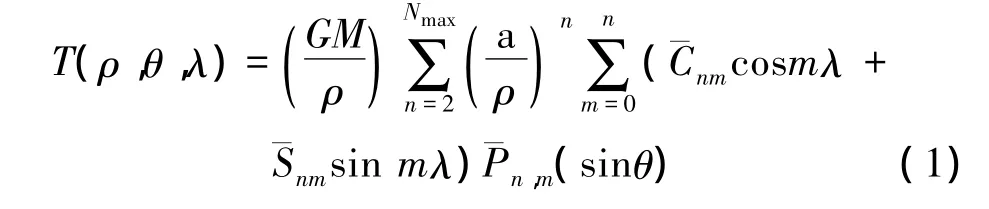
由布隆公式,可得地面点P(ρ,θ,λ)高程异常为
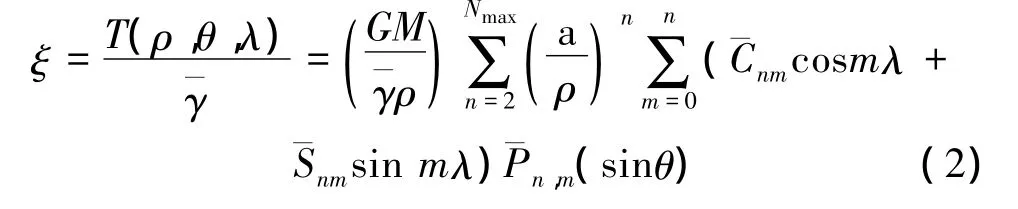
式中,Cnm,Snm为完全规格化的n阶m次地球引力位系数;Pnm为完全规格化的n阶m次勒让德函数;GM为地心引力常数;a为参考椭球长半径;ρ,θ,λ分别为地心向径、地心纬度和地心精度。γ为平均正常重力,可由下式获取[6]
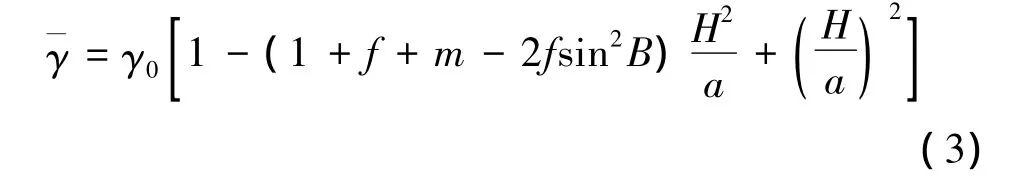
式中γ0为椭球面上的正常重力
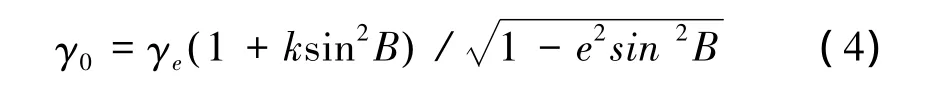
γe为赤道正常重力,B为为大地纬度,e为椭球第一偏心率,f为椭球扁率;m=w2a2b/GM。W为地球自转角速度;b为地球椭球短半径。
2.3 高程转换及残差处理
由GPS定位技术获得某点相对WGS-84椭球面的大地高为H,通过EGM2008模型求解的高程异常为ζ,则该点的正常高为h

在实际应用中,利用上式计算的结果不理想,外符合检验残差较大,不能满足实际需求。由文献[4]可知,这种较大差异是由于某一国家或区域定义的高程基准与EGM2008模型定义的全球高程基准并不能完全精准匹配,存在系统差ΔH。对(5)进行系统差修正,则高程转换公式为
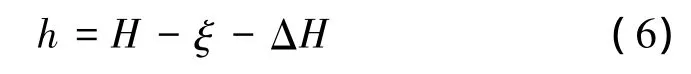
系统差ΔH在不同区域取值不一样,可以利用测区已有的GPS水准点,进行近似求解。假设测区有多个GPS水准点,可以由公式(6)进行简单求解
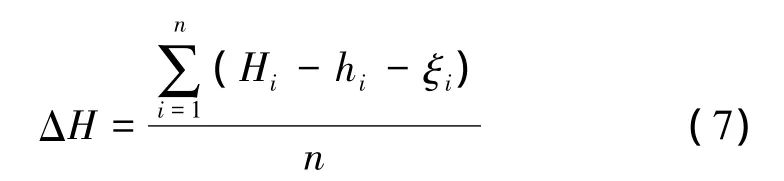
(7)式求取系统差时,需要多个具有代表性分布均匀的GPS水准点,实际应用存在一定局限性。根据高程异常曲面同样均衡性特点,本文采用高差法来消除这种系统误差,高差法是利用在局部区域系统差ΔH相关性,求取高程异常之差后,再按照高差传递求取正常高。GPS点i和j之间的正常高程可以表达为下式

在测区按一定范围,选取一个GPS水准点P作为基准点,其正常高为hp,大地高为Hp,由EGM模型求得高程异常为ξp,其他点按公式(8)进行高差计算,则任意点正常高为
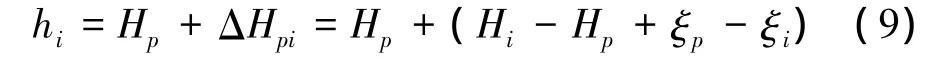
3 计算实例分析
利用新疆某铁路勘测设计中布设的25个GPS水准点对上述方法进行了试验,GPS点高程范围为320~480m之间。采用静态相对定位的方式观测一个时段,时段长度为1 h,采用精密单点定位软件Trip和GAMIT软件分别解算,获取高精度大地高,利用All Trans EGM2008 Caculator软件计算出个各点的高程异常值。分别按照公式(5)直接转换,同时把点GPS01作为公式基准点,分别采用直接转换和高差法进行GPS高程转换。转换正常高与已知实测水准高求差作为转换误差,根据各计算点与基准点GPS01距离L计算允许限差,三等水准和四等水准分别按照计算限差,L单位为km。

表1 转换高程与实测高程较差 m
从表1可以得出,直接法转换正常高程与实测水准高程较差较大,明显可以看出存在系统差。绘制直接法转换高程较差曲线,如图2所示,从图2上可以看出,利用直接法按照公式(5)进行转换的结果存在系统差,本算例数据系统差为0.30m。这与已有研究资料表明的EGM2008模型高程异常在我国西部地区适应性精度平均值0.24m结果相接近,且小于最大值0.55m。
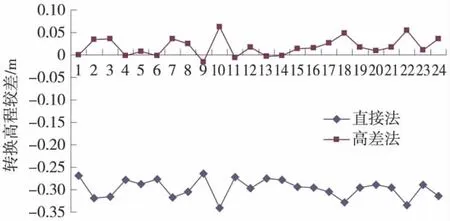
图2 转换高程较差
与三、四等水准限差相比,上述计算点均可满足四等水准要求,除点GPS07和GPS10外均满足三等水准限差,GPS07和GPS10距离基准点GPS01距离超过了10 km。在施测水准困难区域,采用EGM2008模型进行GPS高程转换,可以满足中小比例尺测图要求。
4 总结
采用GPS静态相对定位技术或精密单点定位技术获取大地高后,利用EGM2008模型计算的高程异常,并采用高差法消去EGM2008定义的全球大地水准面与局部似大地水准面的系统差,实现GPS高程转换为正常高,在一定程度上可以取代水准测量。实例验证,采用一个已知高程点作为基准点,在10 km范围内,转换后的高程与实测水准较差可以达到三等水准限差要求,可以满足中小比例尺地形图测图的要求。如果在GPS大地高差转换为正常高差时,能够利用更高精度的中国区域重力场模型,这种方法的精度将进一步提高。
[1]李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009.
[2]2009.EGM2008-WGS84 Version[R].NGA.
[3]刘晓刚,邓禹,叶修松,等.EGM96与EGM2008地球重力场模型精度比较[J].海洋测绘,2010,2010,30(2):55-58.
[4]冯林刚,张锁祥,蒙奎文.基于EGM2008模型的重力观测点GPS高程转换[J].物探与化探,2009,34(4):549-563.
[5]章传银,郭春喜,陈俊勇,等.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报,2009,38(4):283-289.
[6]樊繁,许双安,罗君,等.GPS在大坝倾倒体水平位移监测中的应用.测绘信息与工程,2010,35(6):15-17.
[7]张帝,高雅萍,许双安.GPS技术在矿区沉降监测中的应用[J].测绘信息与工程,2010,37(2):22-28.
[8]许双安,姚宜斌,孔建,等.一种建立回归模型的新方法[J].大地测量与地球动力学,2010(4):117-121.
[9]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2010:76-92.

