一种联合优化算法及其在混沌时间序列预测中的应用
向昌盛,周子英
(1. 湖南农业大学 东方科技学院,湖南 长沙,410128;2. 湖南农业大学 资源环境学院,湖南 长沙,410128)
混沌时间序列预测广泛应用于信号处理、自动控制、金融和负荷预测等领域,其主要包括相空间重构、预测模型选择以及预测模型参数优化等问题[1]。通过相空间重构确定最佳延迟时间(τ)和嵌入维(m),挖掘混沌时间序列数据间的信息量,恢复混沌时间序列原动力系统。预测模型根据重构后的数据进行学习与建模,对未来时刻的值进行预测[2]。相空间重构质量直接影响预测模型的建立与预测结果,主要有自相关联函数法[3]、C−C 法(Coupled cluster method)[4]和时间窗口法[5]等,这些方法性能的优劣因数据不同而各异,且判断标准具有一定主观随意性,可见,目前缺乏一种通用性较强的最佳τ和m的选择方法[6]。较常用的混沌时间序列预测算法有全域法、局域法、神经网络和支持向量机等[7−9]。最小二乘支持向量机(least square support vector machines,LSSVM)是一种基于结构风险最小化原则的机器学习算法,较好地解决了非线性、高维数和局部极小等难题,泛化能力较强,克服了神经网络的过拟合缺陷,在混沌时间序列预测研究中取得很好的应用效果[10]。为此,本研究选择LSSVM作为混沌时间序列的预测模型。LSSVM 模型参数决定了LSSVM的学习和泛化能力,但各参数选择缺乏统一标准和理论指导,各种参数优化算法性能差异很大,目前尚未有一种通用参数优化法则可供参考,LSSVM参数的选择是一个尚待解决的难题[11]。τ,m与LSSVM模型参数相互制约,同时决定了混沌时间序列的预测精度,应联合优化,但现有混沌时间序列预测方法的各参数优化都是独立分开进行,忽略参数间相互关联。针对该缺陷,本文作者提出一种基于遗传算法(genetic algorithm,GA)的参数联合优化方法(GA-LSSVM),并通过混沌时间序列实例对其性能进行验证。
1 相空间重构和最小二乘支持向量机理论
1.1 混沌时间序列的相空间重构
相空间重构把具有混沌特性的时间序列重构成为一种低阶非线性动力学系统,从而近似恢复系统的混沌吸引子[12]。
设观测到的混沌时间序列为:{x(t)}(其中:t=1,2,…,n;n为样本数)。根据Takens定理,可以通过选定合适的τ和m将混沌时间序列时间重构为:
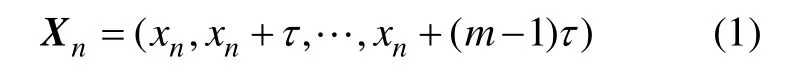
从式(1)可知:相空间重构结果的优劣由τ和m决定。根据Takens定理,对于无限长和无噪声的混沌时间序列,τ可以任意选择,即与m没有关联。但实际上时间序列不可避免地带有噪音且不能保证序列长度足够长,因此,在实际应用中τ的选取对相空间重构的质量有着重要的影响,τ和m相互关联,因此,应该同时选择。
1.2 最小二乘支持向量机
由于支持向量机的复杂度与输入空间的维数无关,而依赖于样本数据的个数,因此,样本数目越大,求解相应的二次规划问题越复杂,计算速度越慢,进而限制支持向量机的应用范围[13]。Suykens等在标准支持向量机的基础上提出了最小二乘支持向量机(LSSVM),将标准支持向量机型中的损失函数设定成误差平方和,把不等式约束改成等式约束,减少待定参数,又将求解二次规划的问题转化成线性 KKT(karush kuhn kucker)方程组的求解,降低了求解的复杂性,拓宽了支持向量机的应用空间[14]。
对于训练样本集{(xi,yi)},(i=1,2,…,n),xi和yi分别表示样本输入和输出, xi∈Rn,yi∈R,通过非线性映射函数 φ(·)将样本映射到高维特征空间,从而获得最优线性回归函数:
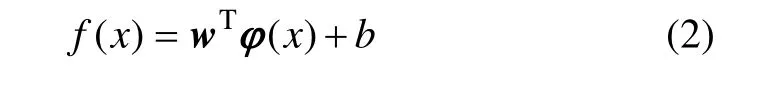
式中:w为特征空间的权值向量;b为偏置量。
根据结构风险最小化原则,式(2)问题求解的LSSVM回归模型为:
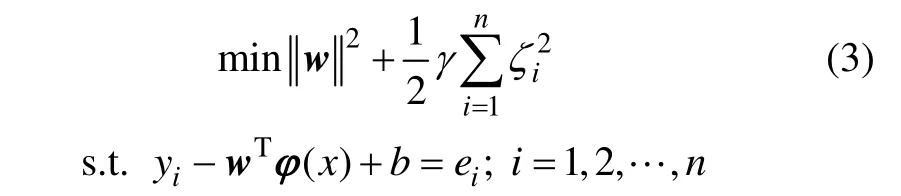
式中:γ为惩罚参数,用于平衡训练误差和模型复杂度;ei为实际值与回归函数间的误差。
通过引入拉格朗日乘子(Lagrange multiplier)将上述约束优化问题转变为无约束对偶空间优化问题,即:
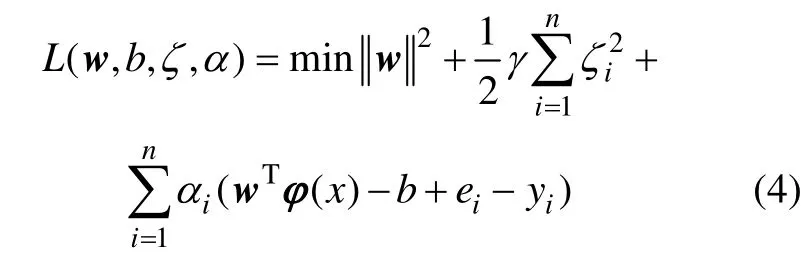
式中:αi为拉格朗日乘子。
根据Mercer条件,核函数定义如下:
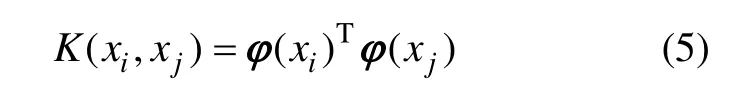
本研究选择径向基核函数作为LSSVM核函数,径向基核函数为:
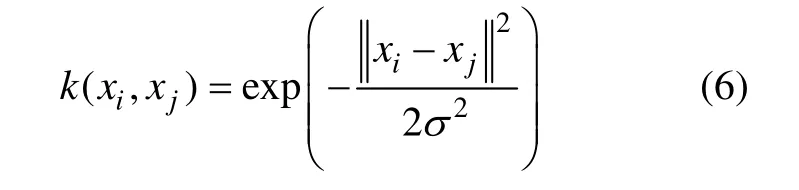
最后LSSVM回归模型为:
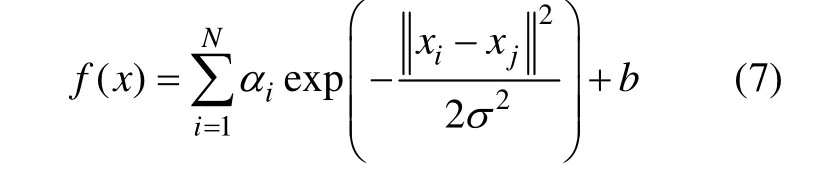
其中:σ表示径向基核数宽度。
由上述LSSVM回归建模过程可知,基于径向基核函数的LSSVM学习性能主要取决于γ和σ。
2 影响混沌时间序列预测结果的参数分析
基于LSSVM的混沌时间序列预测模型需要优化的参数为τ,m,γ和σ。表1~4所示分别表示同一混沌时间序列(Mackey-Glass)在不同参数下的预测精度比较结果。
通过对表 1~4结果进行比较可知:相空间重构(τ和 m)和 LSSVM 参数(γ和 σ)对预测结果的影响均很大,且二者互相关联,然而传统算法将两者分开单独进行优化,割裂了两者间的联系,这样就存在无法确定先优化τ和m还是γ和σ的缺陷,且优化其中一个时需随机地确定另一个,这样即使轮流进行优化也不能保证两者同时达到最优,导致有时预测效果不理想[15]。为了获得最优的混沌时间序列预测结果,就需要使τ,m,γ和σ同时达到最优,因此,它们应该进行联合优化。
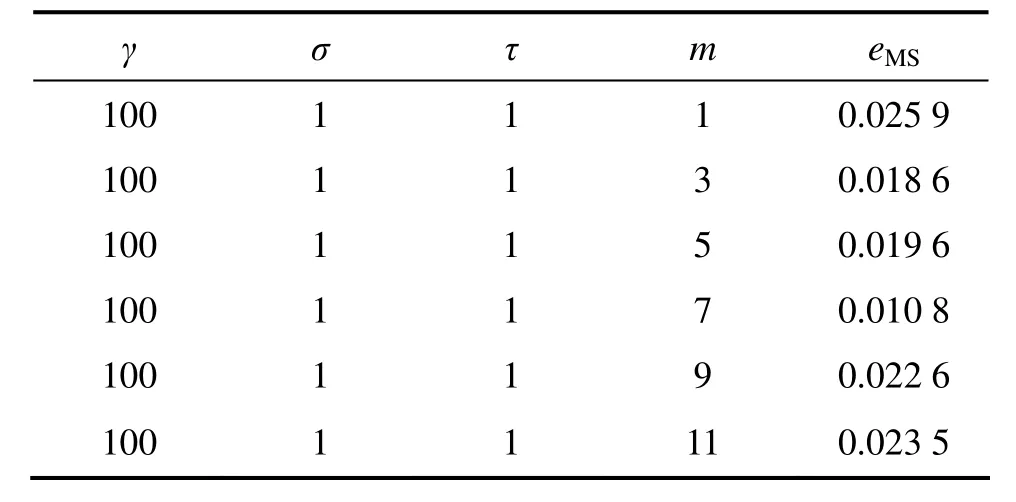
表1 m对预测精度的影响Table 1 Influence of m on prediction precision
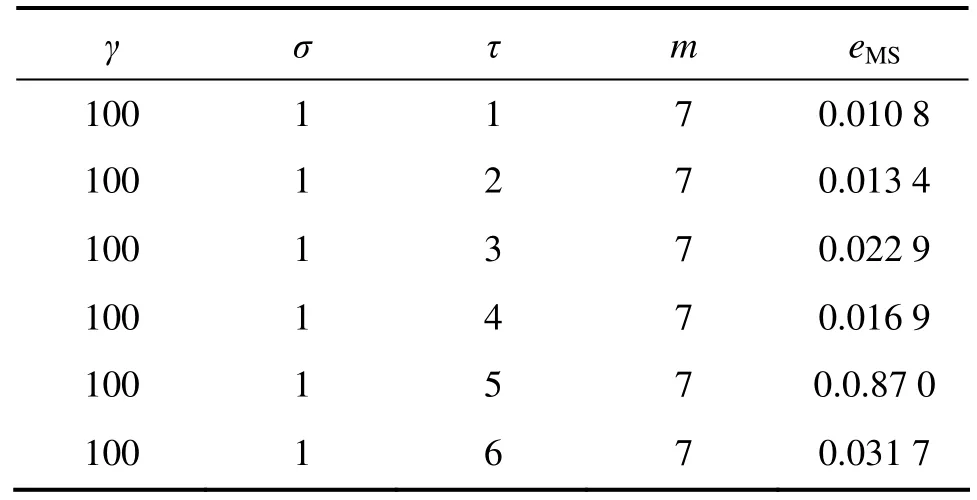
表2 τ对预测精度的影响Table 2 Influence of τ on prediction precision
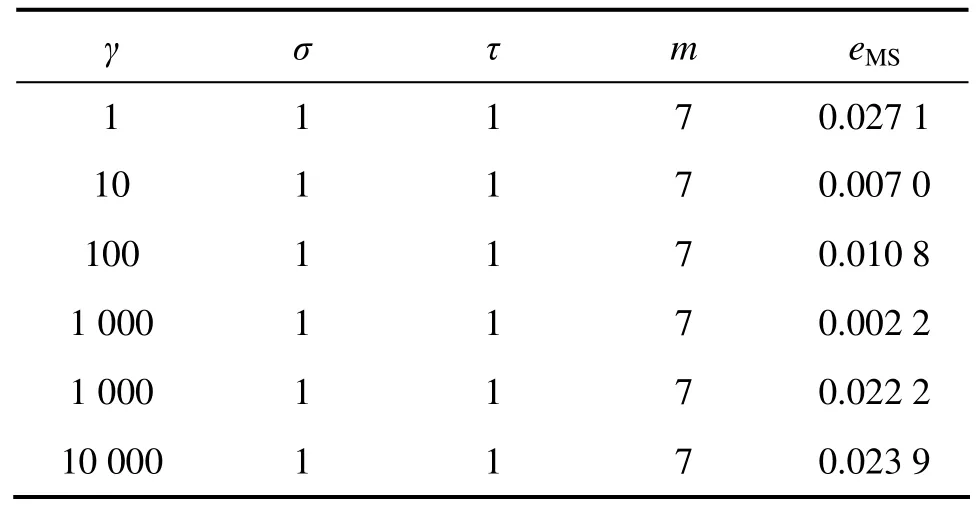
表3 γ对预测精度的影响Table 3 Influence of γ on prediction precision
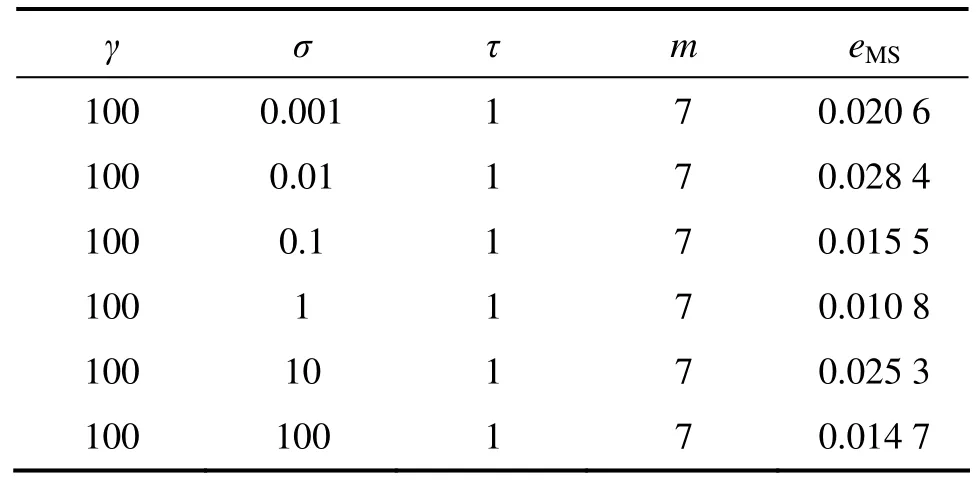
表4 σ对预测精度的影响Table 4 Influence of σ on prediction precision
3 参数联合优化设计
τ,m,γ和σ的联合优化显然是一个多参数组合优化问题,如果采取穷举法进行求解,计算量将十分巨大以至于有时无法实现,为了减少参数优化复杂度,传统上是依次找到每个参数的最佳水平,将多参数优化问题转化为单参数优化问题,忽略了参数之间的交互作用,因此,将每个参数的最佳水平组合在一起未必是全局最优参数组合。GA利用生物遗传学的观点,通过自然选择、交换和变异等机制实现种群的进化,具有隐含的并行性和强大的全局搜索能力,可以在较短时间内搜索到全局最优解[16]。因此,本研究采用GA对τ,m,γ和σ进行联合优化。
3.1 个体编码与设计
个体采用二进制编码方式,由于选择径向基核函数作为 LSSVM 核函数,因此,GA个体由 τ,m,γ和σ 4部分组成。个体的前a位代表τ,中间b位代表m,中间c位代表γ,最后d位代表σ,如图1所示。

图1 个体设计Fig.1 Design of individuals
个体中的各位二进制串通过式(8)转换为十进制表示的模型实际参数。
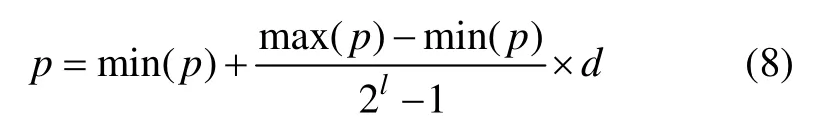
式中:p为参数的十进制值;min(p)为参数的最小值,max(p)为参数的最大值;l为参数的二进制位串长度;d为参数的二进制位串的十进制值。
3.2 种群初始化
基本遗传算法的初始种群是随机产生的,初始种群分布空间具有很大的不确定性和不均匀性,不能很好地包含全局最优解的信息,易发生过早收敛现象,出现局部最优问题。为了防止该问题发生,本研究采用均匀设计来产生初始种群,确保初始种群的多样性与个体分布的均匀性。
3.3 适应度函数
遗传算法的搜索目标是找到最适合的τ,m,γ和σ,从而提高混沌时间序列的预测精度,降低预测误差,因此适应度函数应与模型预测能力有关,设第j组参数的预测均方误差(Mean squared error,eMS)为
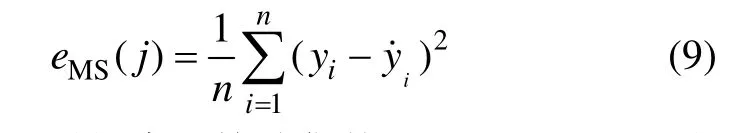
式中:n为混沌时间序列检验集数目;yi和y˙i分别为混沌时间序列的实际值和预测值。第j个个体的适应函数定义为:
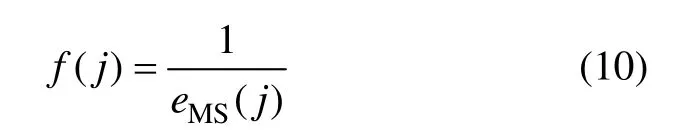
3.4 遗传算子设计
3.4.1 选择算子
计算个体适应度值,按照适应度值大小进行排序,采用个体保持策略选择R个最优个体进入下一代,其余n−R个个体采用交叉、变异操作产生新的个体进入下一代。
3.4.2 交叉算子
在个体的4部分上分别选择4个交叉点,然后与另外一个个体相对应部分进行交叉操作。交叉完毕后,对生成的子个体进行检验,验证其是否在参数取值范围内,若不在参数取值范围内,则重新进行交叉操作。
3.4.3 变异算子
对个体的4部分分别采用传统翻转变异方法进行变异操作,随机选取个体上的1位,按照0变成1,1变成0的规则进行变异操作,然后,检验变异后个体是否在参数取值范围内,若不在参数取值范围内,则重新进行变异操作。
3.5 参数联合优化具体步骤
首先,将GA产生初始种群作为预测模型的参数,包括τ,m,γ和σ,利用这些参数分别进行相空间重构和LSSVM模型训练和预测,返回一系列测试误差eMS,然后计算每个个体适应度,通过选择、交叉和变异等遗传操作产生下一代参数种群,再利用该子代种群进行上述操作,直到满足GA结束条件为止,最后利用得到的最优参数进行建模和预测。参数联合优化具体步骤为:
(1) 确定全部参数组成的原始特征空间,且进化代数t=0。
(2) 对参数τ,m,γ和σ进行编码。
(3) 采用均匀设计产生含有m个体的初始种群。
(4) 将个体反编码成为实际参数,根据τ和m对混沌时间序列数据进行重构,然后,LSSVM 根据参数γ和σ进行训练和预测,记录每组参数的预测精度,并计算每个个体的适应度值。
(5) 从群体中选择预测性能最好的R个个体予以保留并进入下一代,其余的个体进行选择、交叉和变异操作,从而产生新的种群,t=t+1。
(6) 判断是否满足结束条件,若满足,则进入步骤(7);否则,返回步骤(3),继续重复上述操作。
(7) 输出最佳个体中的τ,m,γ和σ。
(8) 采用最优τ和m重构混沌时间序列数据,采用最优γ和σ作为LSSVM的参数对重构的时间序列进行训练建模并预测,最后得到最佳预测结果。
4 仿真实验
4.1 模拟混沌时间序列的预测
4.1.1 Mackey-Glass时间序列预测
采用Mackey-Glass混沌时间序列对GA-LSSVM有效性进行验证,Mackey-Glass混沌时间序列定义如下:
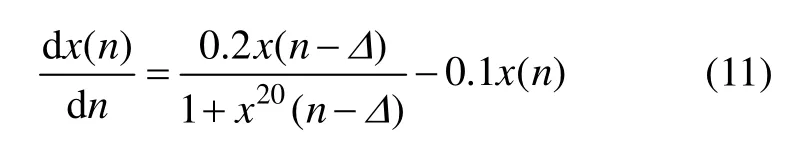
式中:Δ为时滞参数,当Δ≥17时呈现混沌性,且Δ越高,混沌程度越高[17]。
本研究取 Δ=30,应用 4阶龙格库塔法产生Mackey-Glass混沌时间序列,去掉前2 000个暂态点,然后取10 000个数据点作为实验样本,前8 000个数据作为训练集,用于建模;中间1 500个数据作为验证集,用于检验模型最优参数有效性;最后500个数据作为测试集,检测模型的泛化能力,实验数据如图2所示。
通过参数联合优化方法,获得最优参数为:τ=1,m=5,γ=100和σ=0.625,利用最优参数对测试集进行预测,预测值与实际输出比较如图3所示。由图3可见:最优参数的预测值与实际值较吻合,表明本研究提出的 GA-LSSVM 参数联合优化方法是有效的,且预测精度相当高。
4.1.2 加噪的Mackey-Glass时间序列预测
为了更进一步验证本研究提出算法的鲁棒性和可靠性,采用 GA-LSSVM 对加高斯白噪声的Mackey-Glass混沌时间序列预测进行仿真实验,其预测结果如图4所示。由图4可见:GA-LSSVM对加噪的Mackey-Glass混沌时间序列的预测精度也较高。实验结果表明:GA-LSSVM的泛化推广能力强,具有很强的鲁棒性。
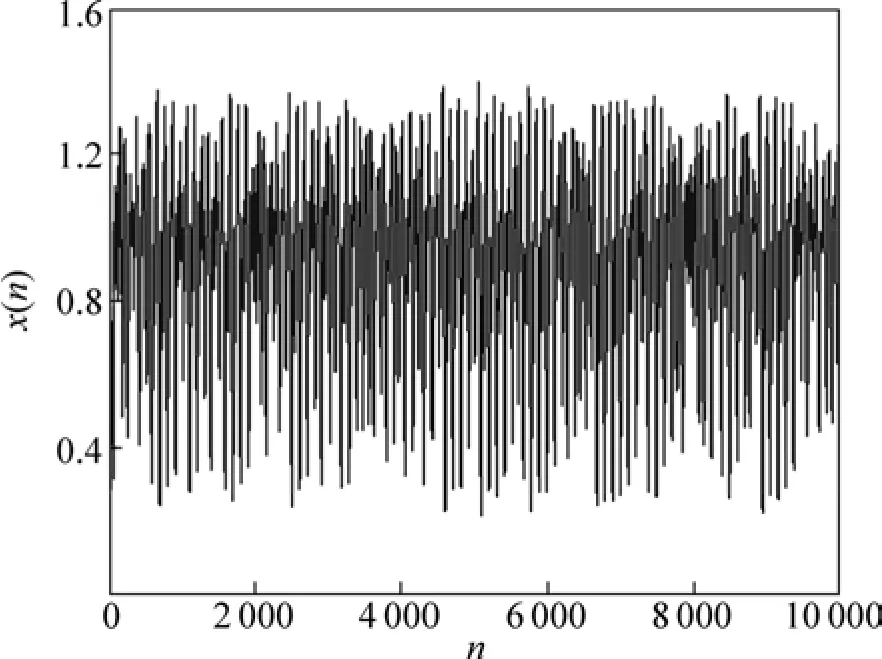
图2 Mackey-Glass混沌时间序列Fig.2 Mackey-Glass chaotic time series
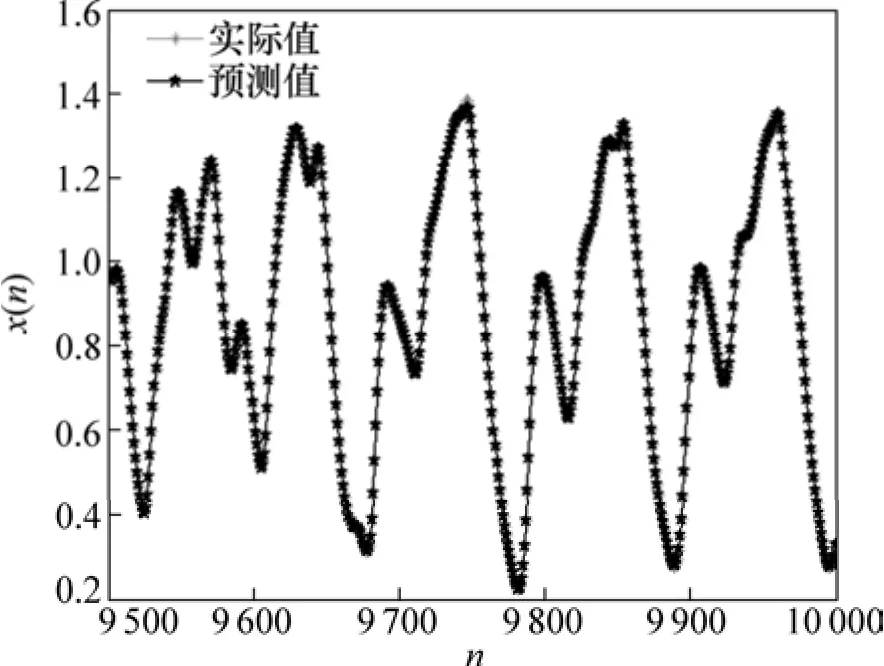
图3 GA_LSSVM对Mackey-Glass的预测结果Fig.3 Prediction results of Mackey-Glass time series by GA_LSSVM
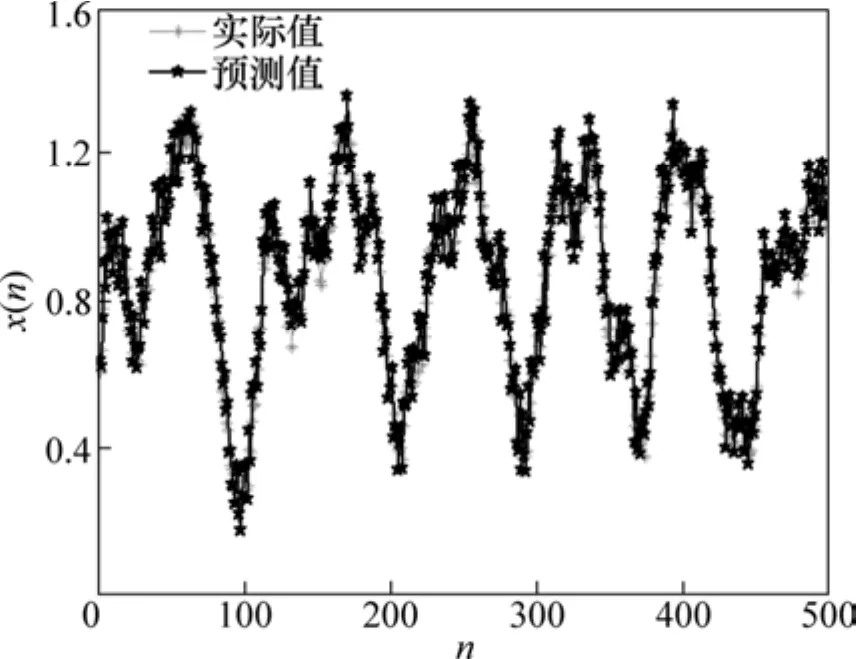
图4 GA-LSSVM对加噪Mackey-Glass的预测结果Fig.4 Prediction results of Mackey-Glass time series with noises by GA-LSSVM
4.2 实际混沌时间序列的预测
为了进一步检测参数联合优化方法在实际应用中的混沌时间序列预测效果,采用太阳黑子月平均数和网络流量对其进行测试实验。
4.2.1 太阳黑子月平均数预测
太阳黑子数据来自 SIDC(Solar influences data analysis center),具体实验数据为1749—2008年太阳黑子的月平均数,数据分成3部分:1749—1950年数据作为训练集;1951—2000年数据作验证集;2001—2008年数据作为测试集。为了使参数联合优化方法的预测结果更具说服力,选择C−C-LSSVM模型作为对比模型,其首先采用C−C方法确定τ和m,然后采用LSSVM进行预测,LSSVM参数采用GA优化。
2种模型对太阳黑子月平均数测试集的预测结果如图6所示。从图6所示的对比结果可知:GA-LSSVM预测结果明显优于 CC-LSSVM。实验结果进一步表明,本研究提出的相空间重构与预测模型参数联合优化思路是有效的和正确的,其预测精度比单独分开优化方法的高,很好地解决当前混沌时间序列预测过程中存在的参数优化问题。
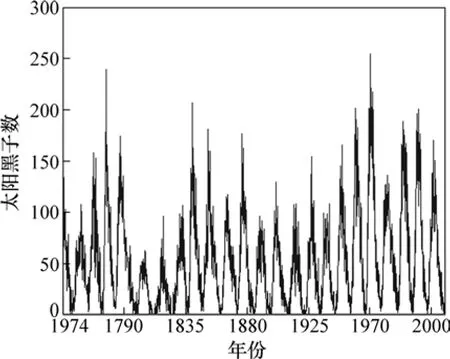
图5 太阳黑子月平均数Fig.5 Monthly average sunspot numbers
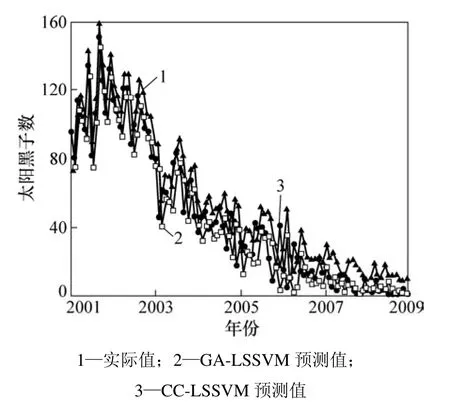
图6 两种模型的太阳黑子月平均数预测结果对比Fig.6 Comparison of monthly average sunspot numbers prediction results
4.2.2 网络流量的预测
网络流量变化具有时变性、非线性和高度自相似性,是一种高度混沌的系统,网络流量数据来自Http://newsfeed.ntcu.net/~news/2008/,共收集到1 000个网络流量数据点,如图7所示。将数据分成3部分:前800个数据作为训练集,中间150个数据作为验证集,最后50个数据作为测试集。
采用CC-LSSVM和BP神经网络(BPNN)作为对比模型,其中BPNN采用C−C进行相空间重构,其参数采用GA进行优化,3种模型对测试集的预测结果如图8所示。从图8所示的对比实验结果可知:本研究提出的混沌时间预测模型的网络流量预测值与实际更加吻合,预测精度比对比方法的高,是一种高精度的混沌时间序列预测方法。
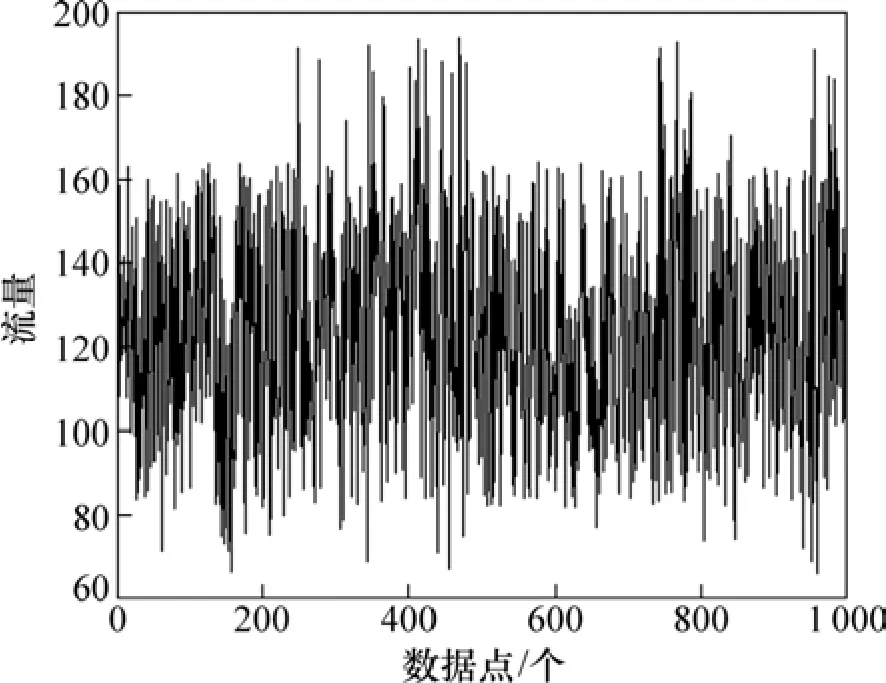
图7 网络流量数据Fig.7 Network traffic data
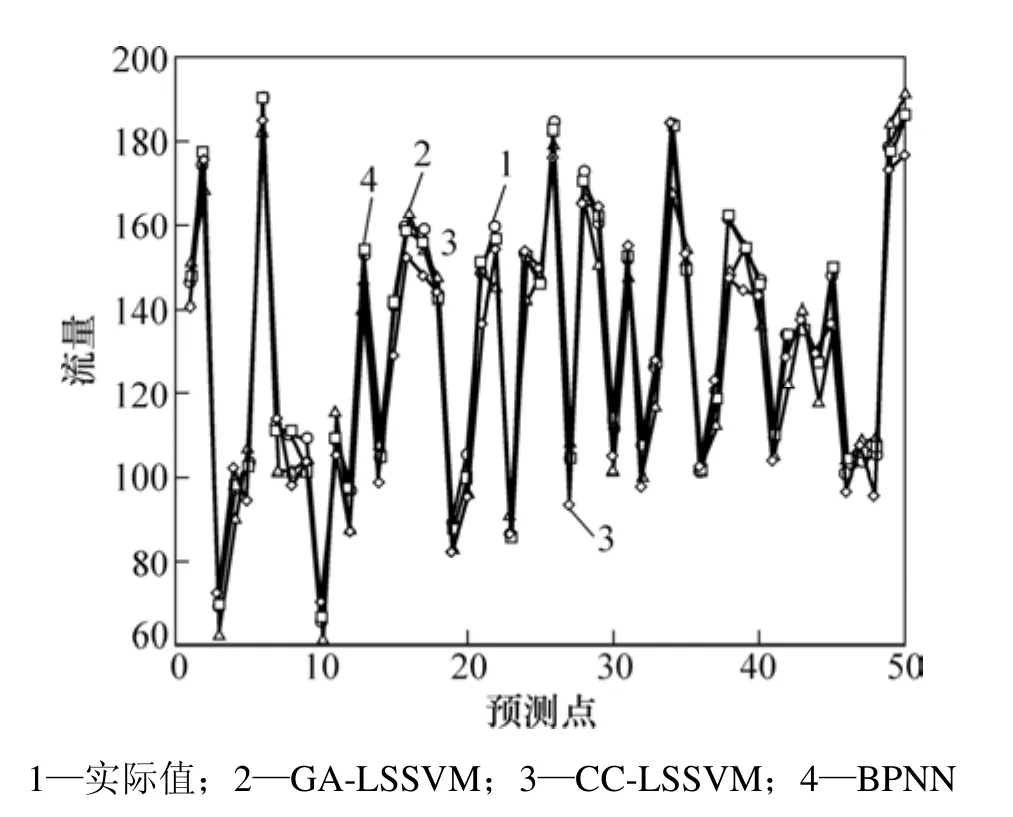
图8 各模型网络流量的预测结果比较Fig.8 Comparison of network traffic prediction results by different models
5 结论
(1) 对影响混沌时间序列模型预测性能的参数进行深入分析,利用参数间的相互联系,提出一种基于遗传算法的参数联合优化方法,并通过混沌时间序列实例对其有效性和优越性进行了验证。
(2) 参数联合优化的模型性能明显优于参数单独优化的模型,参数联合优化方法大幅度提高混沌时间序列的预测精度,为混沌时间序列参数寻优问题提供了一种新的解决思路。
[1]Masoud M, Caro L, Masoud S, et al. Real-time identification and forecasting of chaotic time series using hybrid systems of computational intelligence[J]. Neural Computing & Applications,2009, 18(8): 991−1004.
[2]Albano A M, Muench J, Schwartz C, et al.Correlation-dimension and autocorrelation fluctuations in epileptic seizure dynamics[J]. Phys Rev, 2002, 65(3):1921−1926.
[3]Silva C G. Time series forecasting with a nonlinear model and the scatter search meta-heuristic[J]. Information Sciences, 2008,178(16): 3288−3299.
[4]Kim H S, Eykholt R, Salas J D. Nonlinear dynamics, delay times and embedding windows[J]. Physica D, 1999, 127(10): 48−60.
[5]张淑清, 贾健, 高敏, 等. 混沌时间序列重构相空间参数选取研究[J]. 物理学报, 2010, 59(3): 1576−1582.ZHANG Shu-qing, JIA Jian, GAO Min, et al. Study on the spatial parameters selection of chaotic time series reconstruction[J]. Acta Physica Sinica, 2010, 59(3): 1576−1582.
[6]修春波, 刘向东, 张宇河. 相空间重构延迟时间与嵌入维数的选择[J]. 北京理工大学学报, 2003, 23(2): 219−224.XIU Chun-bo, LIU Xiang-dong, ZHANG Yu-he. Selection of embedding dimension and delay time in the phase space reconstruction[J]. Journal of Beijing Institute of Technology:Natural Science Edition, 2003, 23(2): 219−224.
[7]WANG Wen-sheng, JIN Ju-liang, LI Yue-qing. Prediction of inflow at three gorges dam in yangtze river with wavelet network model[J]. Water Resources Management, 2009, 23(13):2791−2803.
[8]MA Jun-hai, CHEN Yu-shu, XIN Bao-gui. Study on prediction methods for dynamic systems of nonlinear chaotic time series[J].Applied Mathematics and Mechanics, 2004, 25(6): 605−612.
[9]ZHANG Jun-feng, HU Shou-song. Chaotic time series prediction based on multi-kernel learning support vector regression[J]. Acta Physica Sinica, 2008, 57(5): 2708−273.
[10]WU Qiong, LIU Wen-ying, YANG Yi-han. Time series online prediction algorithm based on least squares support vector machine[J]. Journal of Central South University of Technology,2007, 14(3): 442−446.
[11]Ayat N E, Cheriet M, Suen C Y. Automatic model selection for the optimization of the SVM kernels[J]. Pattern Recognition,2005, 38: 1733−1745.
[12]梁昔明, 阎纲, 李山春, 等. 基于最小二乘支持向量机和混沌优化的非线性预测控制[J]. 信息与控制, 2010, 39(2): 129−135.LIANG Xi-ming, YAN Gang, LI Shan-chun, et al. Nonlinear predictive control based on least squares support vector machines and chaos optimization[J]. Information and Control,2010, 39(2): 129−135.
[13]ZHONG Wei-min, PI Dao-ying, SUN You-xian. Support vector machine based nonlinear model multi-step-ahead optimizing predictive control[J]. Journal of Central South University of Technology, 2005, 12(5): 591−595.
[14]PAN Jin-Shui, HONG Mei-Zhu, ZhOU Qi-Feng, et al.Integrated application of uniform design and least-squares support vector machines to transfection optimization[J]. BMC Biotechnology, 2009, 9(1): 52−57.
[15]杨虞微, 左洪福, 陈果. 支持向量机时间序列预测模型的参数影响分析与自适应优化[J]. 航空动力学报, 2004, 21(4):767−773.YANG Yu-wei, ZUO Hong-fu, CHEN Guo. Influence analysis and self adaptive optimization of support vector machine time series forecasting model parameter[J]. Journal of Aerospace Power, 2004, 21(4): 767−773.
[16]QI Hong-li, ZHAO Hui, LIU Wei-wen, et al. Parameters optimization and nonlinearity analysis of grating eddy current displacement sensor using neural network and genetic algorithm[J]. Journal of Zhejiang University Science A, 2009,10(8): 1205−1212.

