基于小波EMD的柴油机油耗量测量信号去噪处理

刘玉梅，袁文华，彭雨

(邵阳学院 机械与能源工程系，湖南 邵阳，422004)

油耗是柴油机的重要技术性能指标之一，有效油耗能直接反映柴油机的燃油经济性。传统的有效功率测定方法不适于对使用中的柴油机的技术状态进行检测[1−3]。为解决柴油机工作过程中有效油耗的测量问题，文献[4]利用函数链神经网络以及混沌优化理论相结合，对柴油机油耗量测量模型进行优化校正，实现了柴油机油耗量信息连续输出和柴油机工作过程的在线监测与智能控制。然而，柴油机工作过程的复杂性决定了柴油机油耗量测量信号存在白噪声和局部高频化噪声干扰。现有研究存在问题包括：采用傅里叶滤波算法[5]去噪时，在滤除高斯白噪声的同时也会滤除信号中十分重要的高频信息；采用样条拟合方法[6]去噪时，虽可较好地抑制高斯白噪声，但同时会将无关信息引入柴油机油耗量测量信号。小波变换极大模算法的主要缺点是准确度不高[7−8]，而经验模态分解(EMD)方法[9−12]能有效地去除高斯白噪声对采集信号的干扰，而且不删除采集信号中的有用信息，不引入无关信息，消噪效果好，但当测量信号和噪声在本征模函数(IMF)分量是混叠时，往往失效，而小波函数的软硬阈值折中法对混叠的测量信号和噪声处理时效果很好。因此，本文结合软硬阈值折中法和EMD方法，对柴油机油耗量测量信号进行去噪处理，能提高柴油机油耗量测量精度，有一定的工程应用前景。

1 柴油机油耗量测量模型

椭圆齿轮体积流量计的计算公式如下：

式中：F为输出脉冲的频率；Q为体积流量；K为仪表系数。K与计量室结构和磁体数n有如下关系：

式中：k为每个磁体的脉冲数；q为椭圆齿轮每转 1周所排出液体的体积；n为磁体个数。为使检测结果稳定可靠，一般取k=1。流量计结构确定后，q为常数，在同一流量下F与n成正比，n越大，F就越高，分辨率也越高。

为消除由于标定条件和使用条件不同而出现的精度偏差，必须根据实际使用条件对椭圆齿轮体积流量计计量精度进行修正。对于椭圆齿轮流量计，在压力不高(压力小于6.4 MPa)的情况下，压力对精度的影响不大，不需要进行压力修正。这里重点讨论粘度和温度对流量计精度的影响及修正方法。对计量精度的修正实际上是对仪表系数 K(物理意义是流过流量计单位容积的流体所发出的脉冲数)的修正，修正后的仪表系数K′为：

式中：E2为用户介质偏差中值；E1为标定介质偏差中值；αT为流量计壳体膨胀系数；t2为工况介质温度；t1为标定介质温度。

在测得脉冲频率F的情况下，将修正后的仪表系数K′代入式(1)可得被测介质的体积流量：

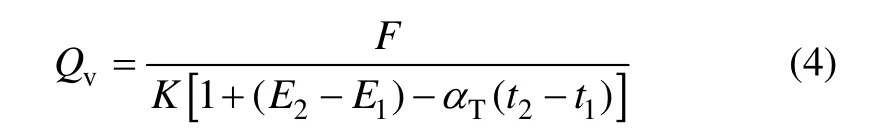
通常，在对柴油油耗体积流量进行密度补偿时，由于柴油压缩系数很小，若工作压力不是特别大，可忽略压力引起的密度变化，而仅考虑温度的影响。当温度变化范围很小(在40 ℃以内)时，柴油密度与温度之间的关系为：

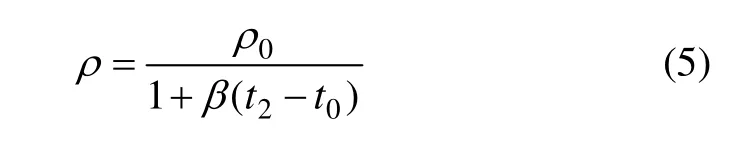
式中：ρ0为温度t0时的柴油密度；β为柴油体积膨胀系数；ρ为工作温度t2时的柴油密度。

当柴油机油耗的体积流量和工况下的密度为已知时，柴油机油耗的质量流量为：

式中：Qm为柴油油耗质量流量；Qv为柴油油耗体积流量；ρ为柴油密度。

将式(4)和(5)代入式(6)，可得工况下柴油流量的计量模型：

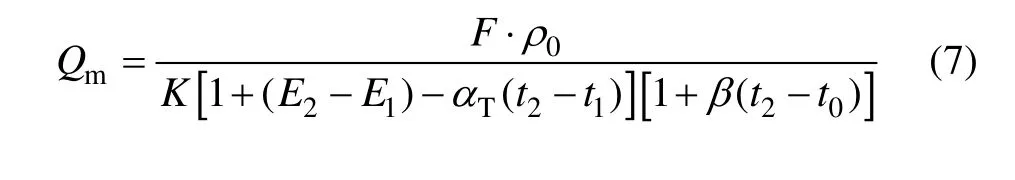
2 基于小波EMD的柴油机油耗量信号去噪处理算法

2.1 小波EMD去噪声处理算法

假设含噪声柴油机油耗量测量信号f(t)可表示为：

式中：s(t)为纯净柴油机油耗量测量信号；n(t)为噪声信号。

借助 EMD方法分解含噪声柴油机油耗量测量信号，可以获得有限数目的分段固有模态函数IMF，具体过程如下：

(1) 找出f(t)所有的极大值点并将其用3次样条函数插值成为原数据序列的上包络线；

(2) 找出f(t)所有的极小值点并将其用3次样条函数插值成为原数据序列的下包络线；

(3) 上下包络线的均值为原数据序列的平均包络线 m1(t)；

(4) 将原数据序列 f(t)减去该平均包络线 m1(t)后即可得到1个去掉低频的新数据序列h1(t)。

一般来讲，h1(t)仍然不是一个平稳数据序列，因此，需要对它重复上述处理过程。重复进行上述处理过程k次，直到所得到的平均包络值趋于0为止。这样就得到了第1个分量C1(t)：

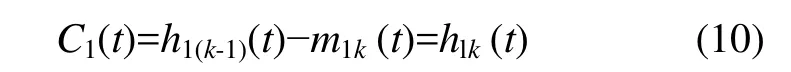
第1个IMF分量代表原始数据序列中最高频的组成成分。将原始数据序列f(t)减去第1个分量C1(t)，可以得到 1个去掉高频组成成分的差值数据序列r1(t)。对 r1(t)进行上述平稳化处理过程可以得到第 2个IMF分量C2(t)，如此重复下去，直到最后1个差值序列 rn(t)不可再被分解为止。此时，rn(t)代表原始数据序列的均值或趋势。差值数据序列可表示为：

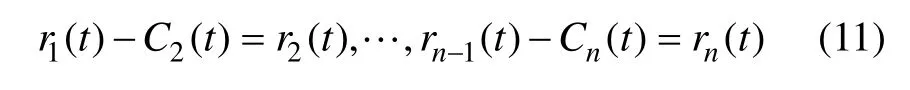
原始的数据序列可由这些IMF分量以及1个均值或趋势表示如下：

为判断所处理信号不再含有IMF分量，并确保每一个IMF具有幅度和频率调制的物理意义， IMF分量的结束循环条件是：

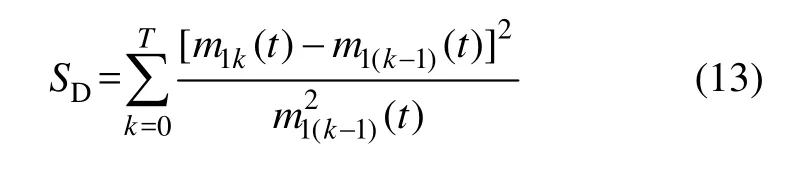
式中：m1k(t)是 IMF 分量提取模块中本次循环过程中求得的平均包络；m1(k−1)(t)是上次循环过程中求得的平均包络；0，…，T是平均包络线所包含的时刻。理想的SD应该在0.2～0.3之间。

因为含噪声柴油机油耗量测量信号数据序列足够长，所以，可根据极值点的情况不断抛弃IMF两端边界失真数据来得到合理的处理结果。每一个IMF分量是代表一组特征尺度的数据序列，“筛”过程实际上是将原始数据序列分解为各种不同特征波形的叠加。需要说明的是：每一个IMF分量既可以是线性的也可以是非线性的。每一个IMF表征了柴油机油耗量测量信号在某一特征尺度上的模态。但是，实际情况表明，柴油机油耗量测量信号和噪声在IMF成分是混叠的，直接利用尺度滤波方法将不能除去噪声。这时，可采用式(14)所示的小波变换中的软硬阈值折中法对每一个IMF成分作阈值处理：

其中：0≤a≤1；Wi为经过阈值处理后的IMF系数；λ为软门限幅函数的阈值，为噪声的方差；N为带噪柴油机油耗量测量信号的长度；a为阈值估计调整因子。

对于一个包含有2个及其以上IMF成分的柴油机油耗量测量信号，其低通尺度滤波结果可表示为：

式中：j=k+1，k+2，…，n，表示带噪柴油机油耗量测量信号被分解为n−k个低频IMF分量。高通尺度滤波结果为：

式中：j=1，2，…，b，表示抽取信号的前b个高频IMF。带通尺度滤波结果为：

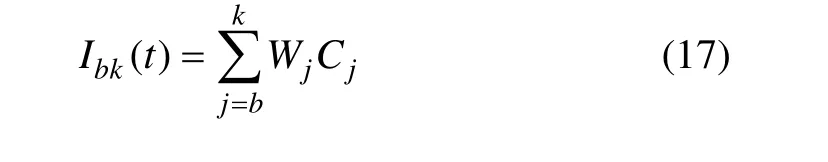
式中：j=b+1，b+2，…，k，表示抽取性能参数信号的中间k−b个中间频率IMF分量。

通过低通尺度滤波方式，可确保柴油机油耗量测量信号的低频成分能被有效地提取出来。通过高通尺度滤波方式，可确保柴油机油耗量测量信号的高频成分能被有效地提取出来。通过带通尺度滤波方式，可确保柴油机油耗量测量信号的中间频率成分能被有效地提取出来。基于小波 EMD的柴油机油耗量测量信号去噪处理过程如图1所示。其中：C1，C2，…，Cn为n阶IMF分量；W1，W2，…，Wn为限幅阈值处理后的分量；K1，K2，…，Km为尺度滤波后剩余的IMF分量。其去噪处理算法由以下步骤组成。

步骤 1：对含噪声柴油机油耗量测量信号进行N=2j+1等分，j为EMD的最大尺度。

步骤 2：对每区内含噪声柴油机油耗量测量信号进行 EMD分解，得到含噪声柴油机油耗量测量信号的各阶IMF分量。

步骤 3：根据含噪柴油机油耗量测量信号的间歇，统计估算得到噪声方差σ。

步骤 4：估计阈值，对各阶 IMF分量进行门限处理。

步骤 5：根据柴油机油耗量测量信号的频谱特征和统计噪声参数，确定尺度滤波方案并进行尺度滤波。

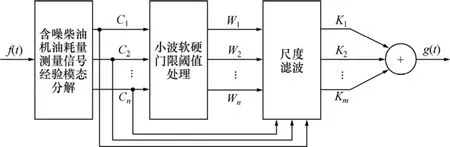
图1 去噪处理过程框图Fig.1 Frame map of denoising disposal process

步骤6：进行信号重构。

步骤 7：继续下一区含噪声柴油机油耗量测量信号处理，重复步骤2～6。

2.2 柴油机油耗量测量信号EMD处理实例

2.2.1 油耗量测量硬件

(1) 计量元件。柴油油耗量测量信号采集如图2所示。椭圆齿轮油耗传感器每转脉冲数为 4，齿轮精度为5，仪表系数K为1.553 脉冲/m3，其他基本参数如表1所示。

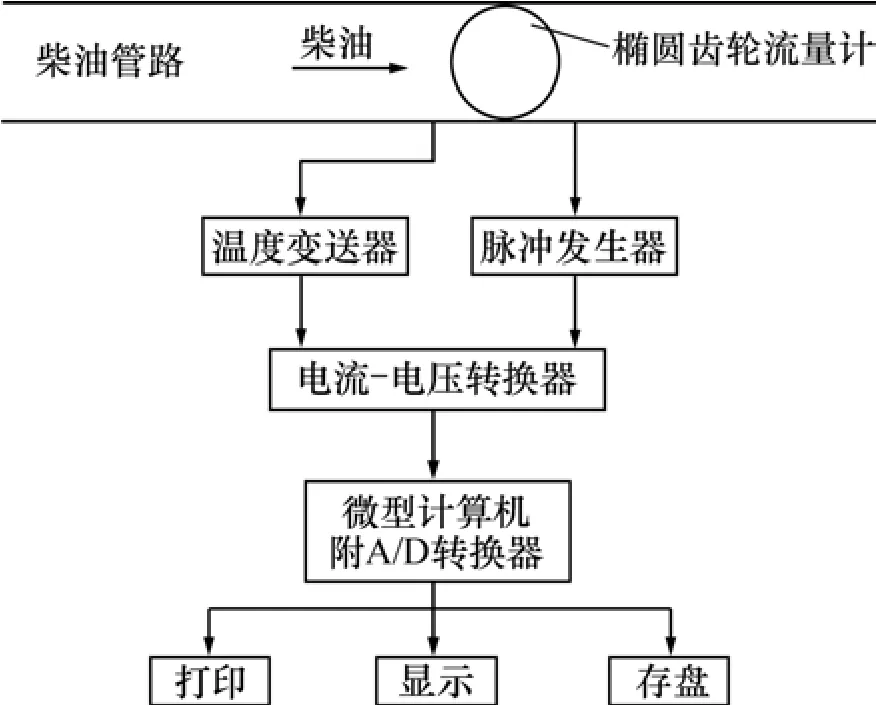
图2 柴油油耗量测量示意图Fig.2 Sketch map of measurement signals of fuel consumption

表1 椭圆齿轮油耗传感器参数Table 1 Parameter of fuel consumption transducer with oval-shaped gear

(2) 微型计算机。微型计算机采用 DELL DIMENSION 4500型，外部设备包括键盘、打印机、显示器和磁盘驱动器。

(3) 外围设备。配套的12位A/D转换器插件板，可将其直接插入主机的标准插座。

(4) 自动化仪表。

1) YKE 202型脉冲发生器；

2) 量程为0～200 ℃的DDZ−Ⅱ型温度变送器转换温度信号，其输出标准电流为4～20 mA DC，经电流—电压转换器转换为1～5 V。

2.2.2 油耗量测量软件

柴油油耗量测量软件采用 VISUAL BASIC语言编写而成，包括以下几部分：

(1) 数据采集和处理系统。根据指令要求，微型计算机接口单元通过其数据接口，将自动化仪表检测到的各种物理量(椭圆齿轮转速和柴油温度)通过传感器转变为电信号，再经过电流—电压转换器作进一步的处理，然后，送给A/D转换器进行A/D转换，最终得到与被测物理量相对应的数字量，从而完成对以上2种不同类型数据的采集。

(2) 体积流量计量系统。测得椭圆齿轮的转速后，利用式(4)可计算出柴油油耗的体积流量Qv。

(3) 柴油机油耗测质量流量测量。利用式(5)对体积流量Qv进行补偿，得到柴油机油耗的质量流量Qm。

2.2.3 油耗量测量数据采集

将此柴油机油耗测量装置安装于待测量的柴油管道中。由于柴油机油路上温度波动较小，黏度变化不大，E2可视为定值。因此，本柴油机油耗测量系统只需在线采集柴油工作温度t2与椭圆齿轮脉冲频率F便可实现柴油流量的在线计量以及流量的实时显示和打印等，使用十分方便。

柴油机油耗测量装置以0.15 s的间隔对上述物理量进行采集和计算，从而得到柴油机油耗量的瞬时值和累积值，得到1 550个如图3所示的含噪声的柴油机油耗量测量信号数据，通过 EMD处理得到如图4所示的IMF1～IMF4分量。分量IMF1～IMF4代表从低阶 IMF分量(即高频段成分占主要部分) 向高阶 IMF分量(即低频段成分占主要部分)的自适应变化，逐次把含噪柴油机油耗量测量信号的频率分量从高到低分解出来。由于 EMD分解方法本身的特点，其基底函数是自适应的，因此，不会像传统的信号分析方法那样受到先验基底函数的影响，所得到的 IMF1～ IMF4分量是信号直接和真实的反映。

测试结果表明：柴油机气缸压力在进气、供油以及燃烧等过程中的较大随机波动性是引起柴油机油耗量测量信号无规则波动的主要原因，而其噪声信号一般为低频信号，故先将含噪声柴油机油耗量测量信号进行EMD分解，再去掉IMF3和IMF4相关成分所对应的干扰因素，对IMF1和IMF2信号进行重构，得到真实柴油机油耗量测量信号图如图5所示。

图3 含噪声柴油机油耗量测量信号Fig.3 Measurement signals of fuel consumption from diesel engine

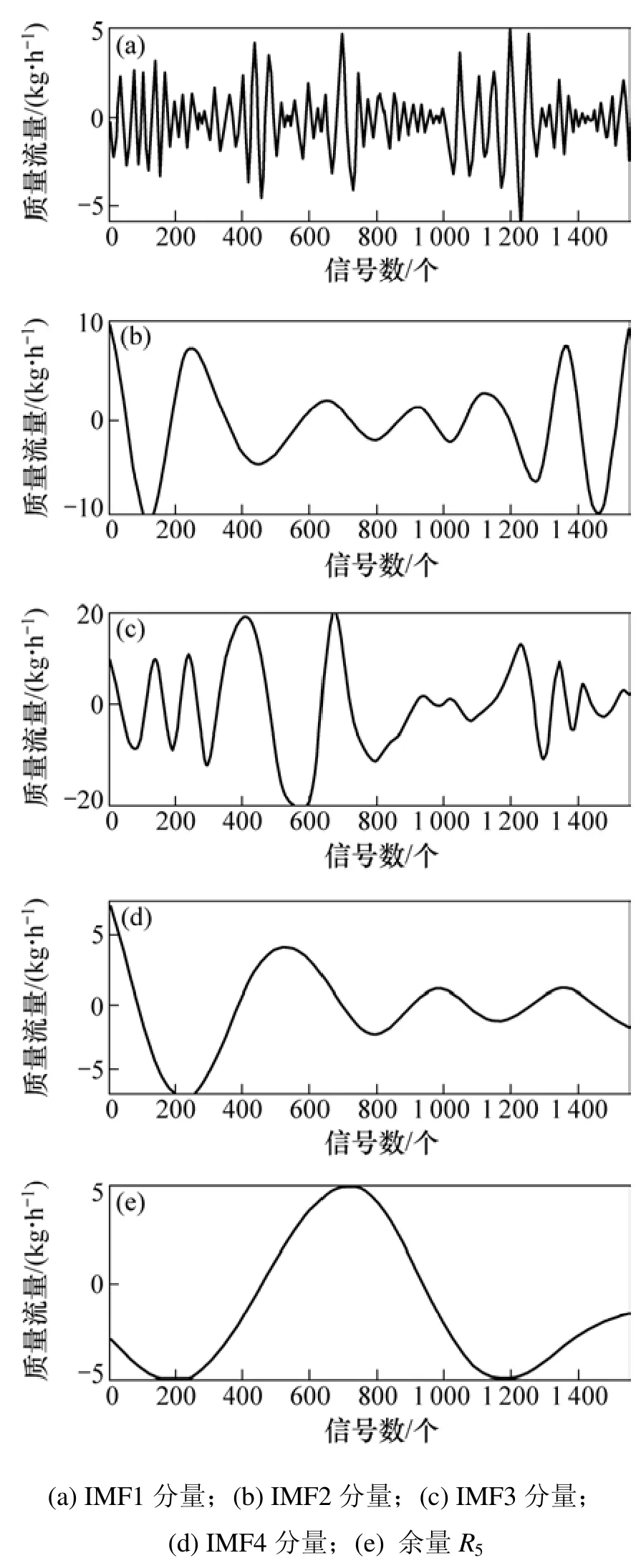
图4 柴油机油耗量测量信号IMF分量Fig.4 IMF components of measurement signals of fuel consumption from diesel engine

图5 柴油机油耗量测量信号IMF分量重构Fig.5 IMF components reconstruction of measurement signals of diesel engine fuel consumption

3 基于小波EMD去噪处理的柴油机油耗量测量对比实验

495柴油机使用0号轻柴油，同时在油路上安装科里奥利质量流量计，用节流阀控制流量进行对比验证实验。以不同体积流量 QV下科里奥利质量流量计测得的柴油质量流量为基准，经小波 EMD去噪处理的柴油机油耗测量相对误差的趋势和文献[4]的柴油机油耗测量相对误差如图6所示。

图6 油耗量测量模型相对误差Fig.6 Relative error from fuel consumption measurement

由图6可看见：体积流量QV在20～70 L/h 之间。文献[4]中的体积流量相对误差在0.85%左右，本文方法的相对误差在0.72%左右且体积流量小于20 L/h。这 2种方法所测试的柴油机椭圆齿轮油耗量测量相对误差均急剧变大，这可能是由于小流量时的泄漏量所占比例较大所致。由此可知：经小波EMD去噪处理的柴油机油耗测量精度很高，完全可以实现柴油机油耗在线测量。

4 结论

(1) 提出了基于小波 EMD的柴油机油耗量信号去噪处理算法，柴油机油耗量测量信号进行 EMD分解后，经阈值处理和尺度滤波，再将剩余IMF分量进行重构，可得到真实反映柴油机油耗量测量信号变化趋势的信号。

(2) 基于小波 EMD去噪处理的柴油机油耗量测量对比实验结果，本文的体积流量相对误差在 0.72%左右，表明小波 EMD算法去噪处理的柴油机油耗测量精度较高，可实现柴油机油耗在线测量。

[1]徐晓明, 郑永光. 失重法智能化瞬态油耗测量仪的研究[J].内燃机工程, 1999, 20(2): 81−83.XU Xiao-ming, ZHENG Yong-guang. A research of an intelligent transient-fuel-consumption meter based on the weightlessness method[J]. Chinese Internal Combustion Engine Engineering, 1999, 20(2): 81−83.

[2]张增建, 傅茂林. 发动机瞬态油耗测量系统研制[J]. 天津大学学报, 2001, 34(4): 550−553.ZHANG Zeng-jian, FU Mao-lin. Development of instantaneous fuel consumption measuring system for the engine[J]. Journal of Tianjin University, 2001, 34(4): 550−553.

[3]方茂东, 郑贺悦. 基于碳平衡法的汽车油耗测量方法[J]. 汽车工程, 2003, 25(3): 294−297.FANG Mao-dong, ZHENG He-yue. Fuel consumption measurement for motor vehicle based on carbon balance method[J]. Automotive Engineering, 2003, 25(3): 294−297.

[4]袁文华, 鄂加强, 龚金科, 等. 柴油机油耗量椭圆齿轮智能测量模型[J]. 农业机械学报, 2006, 37(7): 39−41.YUAN Wen-hua, E Jia-qiang, GONG Jin-ke, et al. An intelligent fuel consumption measurement model using oval-shaped gear for diesel engine and its application[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(7): 39−41.

[5]Alsdorf. Noise reduction in seismic data using Fourier correlation coefficient filtering[J]. Geophysics, 1997, 62(5):1617−1627.

[6]吴先良, 焦丹, 王良之, 等. 从目标瞬态响应中提取极点的样条拟合及有理逼近方法[J]. 中国科学技术大学学报, 1996,26(4): 528−533.WU Xian-liang, JIAO Dan, Wang Liang-zhi, et al. A method for singularity extraction from targets transient response with spline functions and rational approximation[J]. Journal of China University of Science and Technology, 1996, 26(4): 528−533.

[7]焦丹, 徐善驾, 吴先良, 等. 采用频域紧支集正交小波基消除瞬态散射回波中的高斯白噪声干扰[J]. 电子学报, 1999, 27(6):120−122.JIAO Dan, XU shan-jia, WU Xiang-liang, et al. Recovery of signal from transient scattered response contaminated by gaussian white noise based on orthogonal bases of compactly supported wavelets in frequency domain[J]. Acta Electronica Sinica, 1999, 27(6): 120−122.

[8]Mendes O, Domingues M O, Aracy Mendes da Costa, et al.Wavelet analysis applied to magnetograms: Singularity detections related to geomagnetic storms[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2005, 67(17/18):1827−1836.

[9]鄂加强, 王春华, 龚金科, 等. 铜火法冶炼热动力学系统实测数据EMD处理[J]. 中国有色金属学报, 2008, 18(5): 946−951.E Jia-qiang, WANG Chun-hua, GONG Jin-ke, et al. Process on measurement data from copper pyrometallurgical heat dynamical system by using of EMD method[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(5): 946−951.

[10]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,1998, 454: 903−995.

[11]LOH Chin-hsiung, WU Tsu-chin, Huang N E. Application of the empirical mode decomposition-Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses[J]. Bulletin of the Seismological Society of America,2001(91): 1339−1357.

[12]Echeverria J C. Application of empirical mode decomposition to heart rate variability analysis[J]. Medical and Biological Engineering and Computing, 2001, 39(4): 471−479.