灾难救援应急物资配送问题的研究现状及发展方向

陈 刚，彭永涛

(西南交通大学 交通运输与物流学院，四川 成都 610031)

近年来各种灾难频发，无论是 2004年的印度洋海啸、2008年的汶川地震，还是 2010年的海地地震及 2011年的日本地震海啸都造成了大量的人员伤亡和财产损失。据统计，全球每年发生的灾难达 500次以上，75 000 人因此而死亡，2亿人受灾[1]。灾难的发生导致大量应急物资需求，而快速准确地将应急物资运送到受灾点是灾难救援的关键，因而应急物资的分配和应急车辆路径的选择成为灾难救援研究的2个核心问题。有关文献从不同角度或分类对应急物流进行了综述[1-2]。从问题类型及解决方法的角度，结合灾难救援应急物资配送问题分类综述，探讨相关问题研究具有重要的现实意义。

1 应急物资分配问题

1.1 基于数学组合方法

基于数学组合方法的应急物资分配问题实际上是出救点选择问题，问题的基本数学描述如下[3]：A1，A2，…，An为 n个应急物资出救点，A 为受灾点，x 为应急物资需求量，Ai的物资可用量为 xi(xi>0)≥x(i=1，2，…，n)，从Ai到 A 需要的时间为ti(ti>0)，设t1≤t2≤…≤tn，要求给出一方案(确定参与应急的出救点及各自提供的应急资源数量)，在满足约束条件下使应急开始时间最早。

国内最早开始研究应急物资分配问题的是刘春林等[4-6]，考虑在应急物资连续供应条件下，分别以应急开始时间最早、出救点数目最少、使应急开始时间不迟于限制期 t 的可能度最大的方案等为优化目标，并通过组合优化、模糊规划、两阶段规划等方法求解模型。这些研究仅限于单受灾点、单物资种类，适合电力供应系统、供暖供气系统及消防救援系统等连续性应急系统，但不适合大规模突发事件的救援活动。此后，国内学者对这个问题进行了深入研究，增加了总费用最小[7]、损失最小或满意度最大[8]等目标，应急物资种类由1种扩展到多种[9]，受灾点也由1个扩展到多个[10]，出救点选择问题研究进展情况如表1所示。

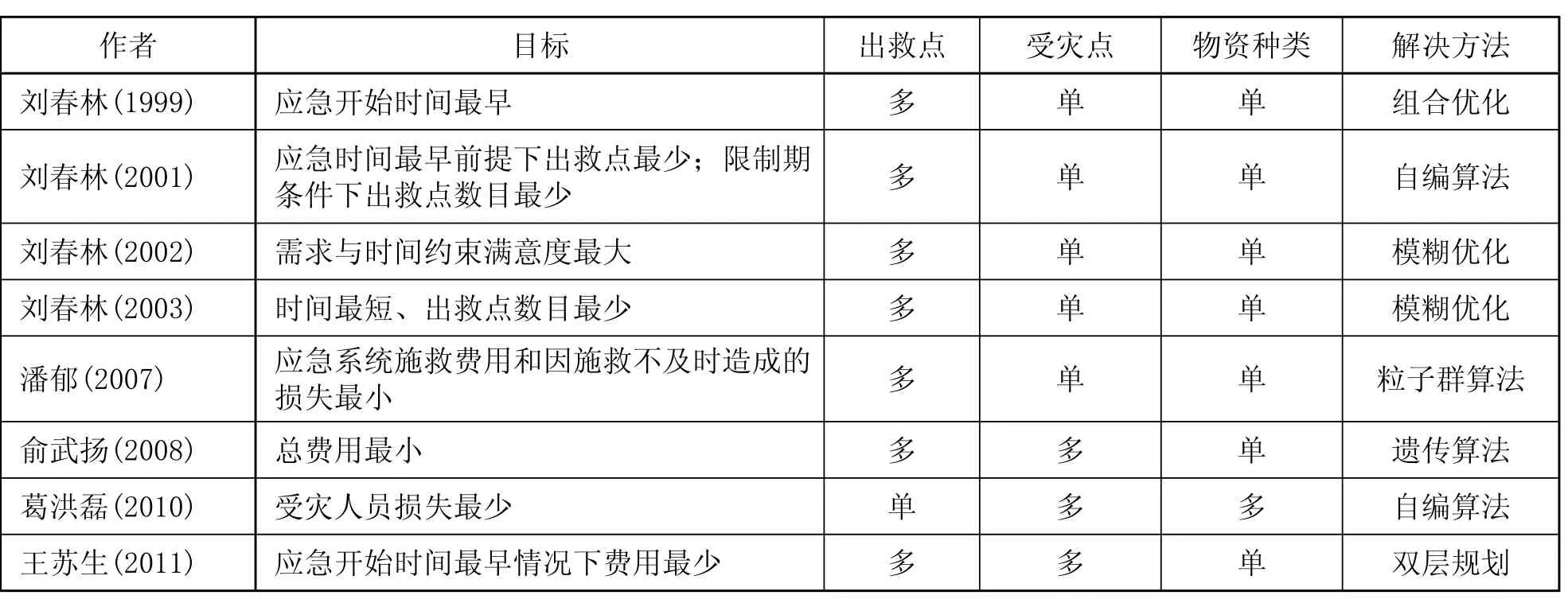
表1 出救点选择问题研究进展情况

1.2 基于模糊聚类方法

Sheu和Chen[11]针对大规模灾难应急物资分配问题，提出了一个3阶段优化算法，第1阶段基于应急物资需求及优先权对灾区进行模糊聚类，第2阶段根据聚类结果进行物资分配，第3阶段根据物资分配结果规划车辆路径。在此基础上，Sheu[12]考虑了时变需求预测和动态供给情形，以台湾地震为研究背景，提出一个由应急物资商、应急物资配送中心及受灾地构成的3层应急物流概念框架，并为关键救援时期响应应急救援需求的应急物流共同配送提出了一个混合模糊聚类优化方法。在其最新研究成果中，Sheu[13]提出一个不完整信息条件下大规模自然灾害动态应急物资需求管理模型，该模型包含基于数据融合的需求预测、模糊聚类受灾区域、对受灾区域分组的优先权进行排序3个步骤。

1.3 基于网络流理论

Haghani和Oh[14]基于时空网络的概念，把灾难救援问题处理为大规模、多商品、多运输方式带时间窗的网络流问题，提出了2种启发式算法，一种算法利用问题的内在网络结构和约束条件将模型分解为子问题求解，另一种算法是利用交互式修复和运行方式，即在每次迭代逐步固定整数变量，直到所有整数变量都为定值。Tzeng等[15]考虑到公平性，提出了一个多目标规划方法，3个目标分别为总成本最小、总运行时间最短及物资需求满足率最大，前2个目标追求的是效益，第3个目标考虑的是公平，保证应急物资配送到所有的需求点。Yi和 Kumar[16]提出用蚁群优化算法解决应急救援活动中的物流问题，把原来的应急物流问题分解为构建车辆路径和多种类物资调度2个阶段，第1阶段在蚁群算法信息素轨迹的引导下建立随机车辆路径，第2阶段建立了基于求解程序 (Solver) 的网络流来解决不同车辆流和物资之间的分配问题。Yan和 Shih[17]认为应急物资配送及中断道路抢修之间是有关联的，为应急物资配送及中断道路抢修构建了时空网络，并以总时间最短为目标建立了一个多目标、多商品的混合整数网络流模型。

1.4 基于其他理论和方法

大规模突发事件往往会中断路网，正常的车辆配送无法进行，Barbarosoglu等[18]为灾难救援运作中直升机任务计划建立了一个双层数学规划模型，上层为战术层，决策直升机队的组合、飞行员的分配及直升机的任务；下层为操作层，决策直升机的路径、装卸配送计划及燃料补充计划。Chang 等[19]基于情景规划方法将洪水应急物流问题描述为2个随机规划模型，借助地理信息系统提出模型的解决方法，为政府部门洪水灾害应急物流提供决策工具。杨继君等[20]设计了应急资源调度的多模式分层网络，提出了基于合作博弈的应急资源调度模型与求解算法，将应急资源的合理调度问题转化为对合作博弈调度模型的核心求解问题。

2 应急车辆路径问题

车辆路径问题 (VRP) 一直是网络优化问题中最基本的问题之一，国内外关于车辆路径问题的研究已经很多。目前大部分 VRP 问题的研究都是在商业背景下，主要以成本最小为目标，应急背景下的 VRP 问题研究不多，主要以应急时间最短或灾区损失最小为目标。Lin 和 Batta[21]结合软时间窗、多周期及分批配送的车辆路径问题，为灾难救援运作关键物品配送问题提出了一个多目标整数规划模型。陈森等[22]利用物资要素和时延要素之间的转换，同时考虑抢修路段和车辆配送，建立了路网结构、车辆路径联合优化模型，提出基于遗传算法和动态规划的求解算法。田军等[23]借助模糊数学中的三角模糊数描述应急物资需求量，利用联系速度时间依赖函数模拟真实的动态路网交通状况，建立应急物资配送动态调度多目标数学模型。徐志宇等[24]建立了分批配送车辆路径模型 (SDVRP)，实现为满足需求最小化、总配送时间最短化、各受灾点失衡度最低化3大目标，但只是通过简单的加权平均将多目标转化成单目标，同时模型也只考虑了单出救点和单物资品种。应急车辆路径问题目前研究的目标约束及算法如表2所示，在这些模型中受灾点的物资需求量都是已知的。

应急车辆路径问题拓展标准如表3所示。从目标函数来看，单目标研究较多，多目标研究较少；从供应特征来看，目前的研究大多数是单出救点，但多出救点、多品种、多周期是未来研究的发展趋势；从需求特征来看，目前的研究大多是需求量确定的情况，也有少部分学者开始考虑模糊或时变需求，并在建模的时候考虑时间窗；从车辆特征来看，应急救援一般都考虑车辆数有限、车容量不同的情况；从运输方式来看，目前还都是以单一的运输方式为主；从解决方法来看，由于都是 NP-hard问题，没有人用精确算法，大部分学者考虑用启发式算法解决问题，仿真研究也相对较少。

3 研究方向

尽管应急物资配送问题的研究已经有了一定的成果，但与大规模突发事件应急救援的实践需要还有一定的差距，未来应急物资配送问题的研究可以主要集中在以下方面。

（1）考虑应急物资需求不确定的情况。目前大多数文献都是考虑需求已知的情况，但灾难发生后，灾区一般都比较混乱，统计工作难以开展，必须通过其他手段来明确各个受灾点的物资需求量。

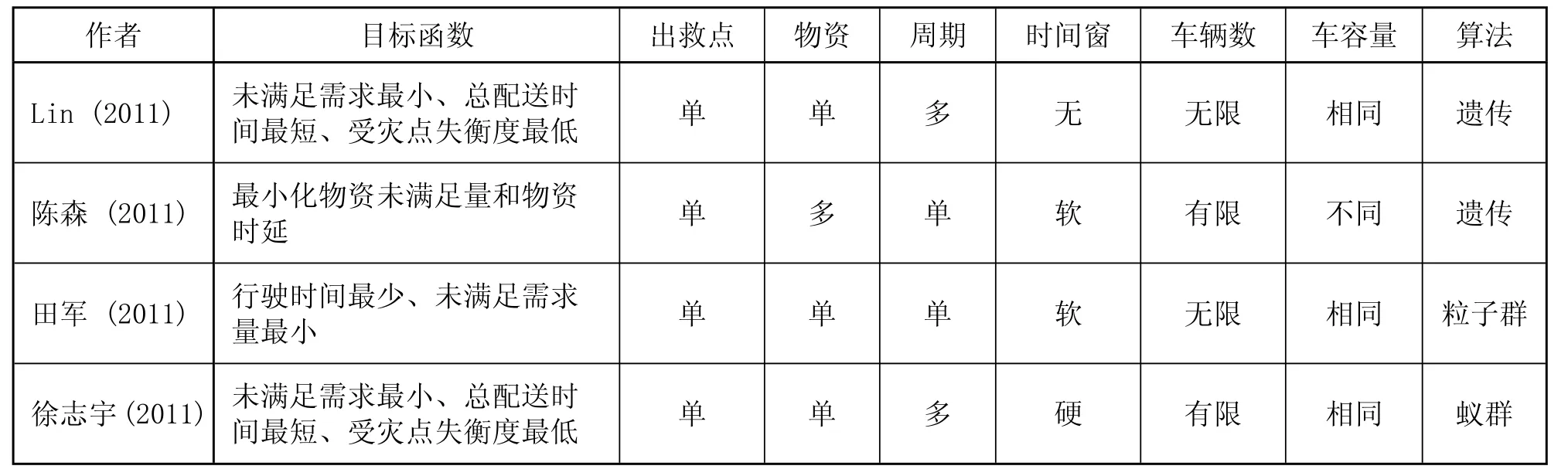
表2 应急车辆路径问题目前研究的目标约束及算法

（2）建立更符合实际灾难救援的应急物资配送模型。目前所查阅到的国内外文献都只考虑了应急救援的某个阶段，未能全面描述应急物资从储备库到配送中心再到受灾点的配送场景，不能完全用来指导应急救援实践。

表3 应急车辆路径问题拓展标准

（3）探索更快速更有效的算法。目前求解应急物流优化模型的算法主要有遗传算法、蚁群算法、粒子群算法等，在解决多目标模型时遗传算法具有较好的适应性，而蚁群算法和粒子群算法在解决单纯的路径问题时优势明显，因此可以进一步研究这几种算法的融合，提出更加快速高效的启发式算法。

（4）结合其他理论研究应急物资分配问题。应急物资分配方案的多利益/多目标冲突决策，与博弈论的最大化个人支出收益思想接近，控制论中的鲁棒规划作为不确定信息处理方法，可以很好地解决应急物资配送问题中的信息不确定性对于决策的影响，这些理论为应急物资配送研究提供了新思路。

[1]Caunhye A M，Nie X，Pokharel S. Optimization Models in Emergency Logistics A Literature Review[J]. Socio-Economic Planning Sciences，2012，46(1)：4-13.

[2]Altay N，Green W G. OR/MS Research in Disaster Operations Management[J]. European Journal of Operational Research，2006(175)：475-493.

[3]刘春林，盛昭瀚，何建敏. 基于连续消耗应急系统的多出救点选择问题[J]. 管理工程学报，1999， 13(3)：13-16.

[4]刘春林，何建敏，施建军. 一类应急物资调度的优化模型研究[J]. 中国管理科学，2001，9(3)：29-36.

[5]刘春林，施建军，李春雨. 模糊应急系统组合优化方案选择问题的研究[J]. 管理工程学报，2002， 16(2)：25-28.

[6]刘春林，沈厚才. 一类离散应急供应系统的两目标优化模型[J]. 中国管理科学，2003，11(4)，27-31.

[7]俞武扬. 大规模应急物资中转运输问题研究[J]. 计算机工程与应用，2011，47(17)：1-3，30.

[8]潘 郁，余 佳，达庆利. 基于粒子群算法的连续性消耗应急资源调度[J]. 系统工程学报，2007，22(5)：556-560.

[9]葛洪磊，刘 南，张国川，等. 基于受灾人员损失的多受灾点、多商品应急物资分配模型[J]. 系统管理学报，2010，19(5)：541-545.

[10]王苏生，王 岩，孙 健，等. 连续性条件下的多受灾点应急资源配置算法[J]. 系统管理学报，2011， 20(2)：143-150.

[11]Jiuh-Biing Sheu Y C. A Novel Model for Quick Response to Disaster Relief Distribution[J].Proceedings of the Eastern Asia Society for Transportation Studies，2005(5)：2454-2462.

[12]Sheu J. An Emergency Logistics Distribution Approach for Quick Response to Urgent Relief Demand in Disasters[J].Transportation Research Part E，2007(43)：687-709.

[13]Sheu J. Dynamic Relief-demand Management for Emergency Logistics Operations under Large-scale Disasters[J].Transportation Research Part E，2010(46)：1-17.

[14]Haghani A，Oh S. Formulation and Solution of a Multicommodity Multi-modal Network Flow Model for Disaster Relief Operations[J]. Transportation Research Part A，1996，30(3)：231-250.

[15]Tzeng G，Cheng H，Huang T D. Multi-objective Optimal Planning for Designing Relief Dilivery Systems[J].Transportation Research Part E，2007(43)：673-686.

[16]Yi W，Kumar A. Ant Colony Optimization for Disaster Relief Operations[J]. Transportation Research Part E，2007(43)：660-672.

[17]Yan S，Shih Y. Optimal Scheduling of Emergency Roadway Repair and Subsequent Relief Distribution[J]. Computer&Operations Research，2009(36)：2049-2065.

[18]Barbarosoglu G，Ozdamar L，Cevik A. An Interactive Approach for Hierarchical Analysis of Helicopter Logistics in Disaster Relief[J]. European Journal of Operational Research，2002(140)：118-133.

[19]Chang M，Tseng Y，Chen J. A Scenario Planning Approach for the Flood Emergency Logistics Preparation Problem under Uncertainty[J]. Transportation Research Part E，2007(43)：737-754.

[20]杨继君，吴启迪，程 艳，等. 面向非常规突发事件的应急资源合作博弈调度[J]. 系统工程，2008， 26(9)：21-25.

[21]Lin Y，Batta R. A Logistics Model for Emergency Supply of Critical Items in the Aftermath of a Disaster[J]. Socio-Economic Planning Sciences，2011，45(4)：132-145.

[22]陈 森，姜 江，陈英武，等. 未定路网结构情况下应急物资车辆配送问题模型与应用[J]. 系统工程理论与实践，2011，31(5)：907-913.

[23]田 军，马文正，汪应洛，等. 应急物资配送动态调度的粒子群算法[J]. 系统工程理论与实践，2011，31(5)：898-906.

[24]徐志宇，彭嘉臻，许维胜. 应急物流的分批配送规划及蚁群优化求解[J]. 计算机工程与应用，2011，47(24)：1-3.