仿射变换对二维蕨类形状控制的研究

包 晔

(浙江水利水电专科学校，浙江 杭州 310018)

0 引言

传统几何学研究对象主要是规则几何体的形状，而新兴的分形几何学研究对象是非规则的几何形体，即分数维物体或图形.事实上，自然界中许多景物，包括树、花、草等植物以及地形、山脉、云彩等都是分数维的，所以研究植物、地形等的计算机图形显示方法具有重要的现实意义.目前国内外对此都已有研究［1－2］.

但是，在经典的二维蕨类植物模拟方面对形状控制方法目前还缺乏研究，本文将重点对二维蕨类植物生成的形状及弯曲方向控制方法进行研究，其主要思想是通过对仿射变换矩阵系数进行调节分析.

1 基本概念

1.1 仿射变换

仿射变换是计算机图形学中几何变换的重要研究内容，也是函数迭代系统(IFS)中经常用到的重要概念.仿射变换包括对图形做绕原点的旋转、放缩、平移以及更一般的变换等.

定义1 二维欧氏空间中的仿射变换为ω:R2→ R2，X= ［x，y］T是此二维空间中的一点，则定义其仿射变换映射像为 X'= ［x'，y］T，即:

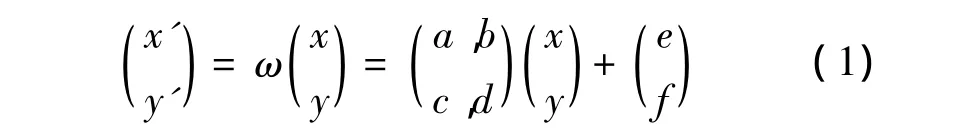
其中:参数 a，b，c，d，e，f均为实系数，它们完全确定一个仿射变换.可以将其分解为平移、旋转和放缩等，用下式表示:

其中，e和f—x和y方向上的平移分量;

θ和φ—分别是绕x、y轴的转角;

r和q分别是x和y方向上的放缩比例因子.

1.2 随机迭代算法

设{X;ω1，ω2，ω3，…，ωN}是一个(双曲)IFS，其中每一个ωi具有一个概率pi＞0，且p1+p2+…+pN=1.选取任一点X0∈X为初始点，然后递归地随机选取下述集合中的一个点作为xn，n=1，2，…，于是有:xn∈ {ω1(xn－1)，ω2(xn－1)，ω3(xn－1)，…，ωN(xn－1)}.

最终得到序列{xn}⊂X，收敛于IFS的吸引子.

2 形状控制方法

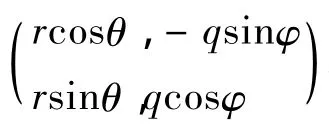
若取仿射变换序列中各仿射变换的系数及该仿射变换被选取的概率见表1.

表1 仿射变换系统选取概率表

其中，迭代次数itn为50000次，仿射变换的个数为 4 个，sx，sy为 x，y 方向的比例系数，r=a，q=b，θ =c，φ =d，e，f即为仿射变换矩阵的相应的值，p为各仿射变换被选取的几率.sx=30，sy=30，count=15.运行后得图1.

若仿射变换的旋转变量c，d相应的值都取反，即见表2.

表2 仿射变换旋转变量选取概率表

则运行后可得图2.可见，蕨类植物的生成方向可由旋转变量θ，φ来控制.

图1 表1仿射变换效果图 图2 旋转后效果图图

可以对a，b，c，d这四个系数逐一分析研究，即保持其他的三个量不变，而让其中的一个系数变化.因为第二个仿射变换出现的几率大，所以在对各仿射变换系数的分析中，只对第二个仿射变换的数据进行变化.

2.1 对系数r进行分析

将数据 a 分别取为:0.851 －0.08，0.851 －0.06，0.851 － 0.04，0.851 － 0.02，0.851，0.851+0.02，0.851+0.04，可得图3.

由图3可知:

x轴上的比例放缩量r

(1)决定蕨类植物叶片绕x轴的旋转(或伸展)幅度，也决定叶片的弯曲程度.

(2)决定各子叶片的间隙的大小.

(3)决定各子叶片的大小.

图3 系数r对蕨类形状控制效果图

2.2 对系数q进行分析，保持其他量不变

将 b 分别取为:0.851 － 0.04，0.851 － 0.02，0.851，0.851+0.02，0.851+0.04，可得图 4.

图4 系数q对蕨类形状控制效果图

由图4可知:

(1)y轴上的比例放缩量q决定蕨类植物叶片在x轴、y轴方向(即屏幕的上下、左右)的伸展幅度，也即决定叶片在x轴、y轴上的放缩.

(2)当q太小时，蕨类植物的叶片会出现脱节现象.

(3)y轴上的比例放缩量q在一定程度上决定叶片的弯曲程度.

2.3 对系数θ进行分析，保持其他量不变

将 c分别取为:0.0 －0.08，0.0 －0.04，0.0，0.0+0.04，0.0+0.08;可得图 5.

由图可知:

(1)θ决定蕨类植物叶片随着从叶根部到叶尖，叶片绕叶茎的扭转程度.即越到叶尖，叶片绕叶茎扭转得越厉害.

(2)θ决定蕨类植物叶片随着从叶根部到叶尖，叶片往哪里偏，即决定茎左右叶子向叶茎的靠拢程度.

(3)θ决定蕨类植物叶片的弯曲程度.

(4)θ决定蕨类植物叶片左右子叶片的尖细(或宽窄)程度.

图5 系数θ对蕨类形状控制效果图

2.4 对系数φ进行分析，保持其他量不变

将 d 分别取为:0.0 －0.02，0.0，0.0+0.02，0.0+0.04，0.0+0.06，0.0+0.08;可得图6.

由图可知:

(1)φ决定蕨类植物的叶片茎的生成方向，即蕨类植物叶片的方向.

(2)φ决定蕨类植物的叶茎与生长在其上的叶片的茎的角度的大小.

(3)φ决定蕨类植物的叶片的弯曲程度.

图6 系数φ对蕨类形状控制效果图

3 结语

本文给出了通过调节仿射变换系数来控制二维蕨类植物生成的形状和弯曲方向的方法，能较好地控制蕨类植物叶片的生成形状.但目前的方法还不能做到精确控制，即不能够控制叶片生成的精确角度和叶片的精确大小，这个问题还有待于进一步研究.

［1］金以文.分形几何原理及其应用［M］.杭州:浙江大学出版社，1998.

［2］倪明田，吴良之.计算机图形学［M］.北京:北京大学出版社，1999.

［3］向世明.OpenGL编程与实例［M］.北京:北京电子工业出版社，1999.

［4］林 勇，宋 征.VisualC++6.0应用指南［M］.北京:人民邮电出版社，1999.