列车自动运行系统的性能指标权重分配方案研究

张 冲 刘晓磊

张 冲:郑州市轨道交通有限公司 助理工程师 450000 郑州

刘晓磊:株洲南车时代电气股份有限公司 助理工程师 412000 湖南株洲

在城市轨道交通自动控制系统中，列车运行控制系统包括列车自动监控子系统ATS(Automatic Train Supervision)、列车自动防护子系统 ATP(Automatic Train Protection)和列车自动运行子系统ATO(Automatic Train Operation)。其中ATO系统在实现高效、安全的自动运行时，要考虑准时性、停车精度、舒适性和节能性这四大性能指标。而无论采用何种控制算法，都不可避免地要表征各性能指标的重要程度，以分配权重系数。

根据各指标特性，合理分配权重是关系到综合评判结果是否科学合理的重要因素之一，直接影响到决策的结果。权重分配的方法很多，大体可以分为主观分配法和客观分配法。由于主、客观分配法均存在一定的局限性，为此，结合它们各自优势，选取层次分析法和马氏距离相结合的层次马氏距离法，以及模糊聚类法和粗糙集法相结合的模糊粗糙集法，使权重分配更为客观准确，以达到更好的ATO控车效果。通过比较两者的分配效果，寻求更适合ATO四大性能指标的权重分配方法。

1 ATO性能指标分析

分析ATO控车过程，将列车运行过程分为牵引、惰行和制动3个阶段，如图1所示。ATO性能指标分析如下。

图1 列车运行阶段划分示意图

1．准时性。列车运行过程中，用列车已运行时间tAC和还需运行预测时间tF与计划运行总时间tT的差，来表征列车准时性△t，即

列车到站后，将列车实际运行总时间tA与计划运行总时间之差，作为本站列车的准时性误差。

参照地铁ATO系统供应商对准时性的要求，设定△t≤2% ×tT，符合准时性运行标准。

2．停车精确性指标。根据相关标准规定，设定停车精度为△s≤0.25 m。列车运行过程中，停车精确性用列车当前运行位移sAc与ATO运行模式曲线的同时刻位移sP之差来表征。

列车到站后，将列车实际停车位置sA与目标停车点sT之差为停车精确性误差。

3．舒适性指标。通过加速度和加速度变化率来衡量，根据列车牵引计算规程，大部分(90%～95%)乘客能容许的加速度变化率限度为乘坐时0.69 m/s3;站立时0.48 m/s3。本文设定列车运行最大加速度变化率为0.48 m/s3。

列车运行过程中，用换挡时的加速度变化率来表征列车舒适性指标。

式中RC为列车当前挡位对应的加速度，RP为列车前一挡位对应的加速度，T为时间周期。

4．节能性指标。根据列车性能可知，列车实际功率是恒定的，故挡位越大，节能性越好。

由于在制动阶段的运行时间是相对恒定的，准时性指标在牵引和惰行阶段需要特别考虑。在牵引和惰行阶段，停车精度指标表现得更多是对运行模式曲线的跟随;在制动阶段，则必须保证列车精确停车;而舒适性和节能性指标是贯穿整个运行过程。通过在启动阶段的最快加速和制动策略，以及尽量延长惰行区段来表征准时性;在运行中，列车换挡应尽量平稳和减少挡位变化来保证舒适性。

2 层次马氏距离法

层次分析法AHP(Analytic Hierarchy Process)强调主观性，是一种基于专家评价为主的研究方法，有利于体现专家经验。并且根据多个专家经验所得的权重，利用马氏距离进行分析，可使各性能指标的权重分配更为合理。

2.1 建立层次分析模型

如图2所示，定义控制列车自动运行为目标层，准时性、停车精确性、节能性、舒适性4个性能指标为准则层，各牵引、制动为方案层。

图2 性能指标层次结构模型

2.2 构造成对比较阵

根据牵引、惰行和制动各阶段中4个性能指标对目标影响的不同，征求4个专家对应于3个阶段分别构造成对比较阵。

2.3 计算权向量并做一致性检验

针对不同专家给出的不同阶段成对比较阵，首先计算出相应的标准化特征向量和最大特征值，再计算衡量一个成对比较阵A(n＞1阶方阵)不一致程度的指标CI:

对于固定的n，随机构造成对比较阵A，其中子样是从1，2，…，9，1/2，1/3，…，1/9中随机抽取的。这样的A是不一致的，取充分大的子样得到A最大特征值的平均值。从有关资料查出检验成对比较阵A一致性的标准RI，如表1所示，它只与矩阵阶数n有关。其中成对比较阵A的阶数 n=4，则 RI=0.90。

表1 平均随机一致性指标RI

根据各专家打分计算得到在不同阶段均有CR＜0.1，故判定成对比较阵均具有满意的一致性。

针对不同专家，在不同阶段的成对比较阵A的随机一致性比率CR:

表2 列车自动驾驶4个专家各阶段各性能指标权重分配

对于各阶段，根据4个专家经验计算得到的4种性能指标权重如表2所示。

在表2各性能指标权重的基础上，再根据马氏距离法计算，使列车具有最佳运行效果的性能指标权重分配方案。

1．根据层次分析法得到由4个专家经验的各权重值组成权重矩阵，包括牵引阶段权重矩阵WM惰性阶段权重矩阵WC和制动阶段权重矩阵WB。

2．分阶段计算各专家给出的各性能指标权重的均值，即牵引阶段均值UM，惰性阶段均值UC和制动阶段均值UC。继而分别计算其协方差矩阵SM、SC、SB，其中，再求出相应的逆矩阵

3．计算马氏距离。分不同的运行阶段，分别对不同专家给出的权重值，用公式(8)计算得到马氏距离Dij。

其中ui、uj分别为第i个和第j个专家给出的各性能指标权重的均值。

4．剔除其中距离最大者，剔除专家人数的20%～30%。本文剔除专家3的经验，再将剩下的3组专家权重重新排序，并进行优化处理得到各指标权重，最后得到风险各层次指标的权重。

各阶段各性能指标权重值如表3所示。

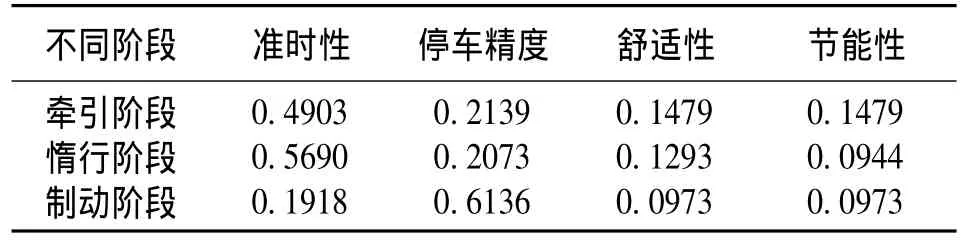
表3 各阶段各性能指标权重值

3 模糊粗糙集法

根据专家经验得到的权重分配，具有一定的主观性，有时不能反映客观实际，对不同的线路条件和不同车况的适应性较差。因此提出基于模糊集与粗糙集的客观分配权重方法。

在列车运行过程中，根据当前列车速度位移与ATO运行模式曲线的误差，也就是实际运行情况与理想运行情况的偏差，利用模糊粗糙集法来确定四大性能指标的权重值，可以实时调整列车的运行策略，完成自动运行功能。

具体而言，在列车运行过程中，一旦实际运行速度位移与ATO运行模式曲线存在较大偏差，需要ATO自动调整时，根据对四大性能指标的分析，预测计算不同挡位下各性能指标的值，并以此为基础使用模糊粗糙集法确定权重值。

1．设定对象集为X={挡位1(x1)，挡位2(x2)，挡位3(x3)，挡位4(x4)}，条件属性值为(准时性xi1，停车精确性xi2，舒适性xi3，节能性xi4)，得到原始数据矩阵A。再按模糊聚类分析的一般步骤进行分类。

2．由“F－统计量”方法确定最佳置信水平阈值λ，找出最佳分类Y={Y1，Y2，…，Yj}，将该分类当作某种决策属性的等价集合。

3．删除条件属性xij(j=1，2，3，4)后得到原始数据矩阵，确定最佳置信水平，找出删除条件属性xij后的最佳分类，得到依次删除xij的分类集 M={M1，M2，…，Mm}。

4．利用粗糙集相关原理，求解每个性能指标的重要程度。利用公式(10)计算2个属性集xi与D之间的依赖程度。

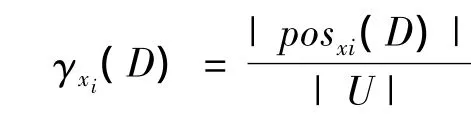
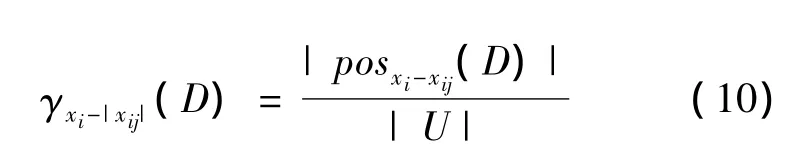
其中posxi(D)=xi_D，|U|表示整个集合对象的个数，D为决策属性即各性能指标。

再根据粗糙集相关理论，求解条件属性xij的重要程度 SGF(xij，xi，D)。

5．根据每个条件属性的重要程度，用归一化处理方法，利用公式(12)分配权重。

在VC++环境下用C语言实现上述方法，最后实时确定各性能指标在不同运行状态和运行环境下的权重值，并运用在ATO运行策略的确定上。

4 仿真实现与结果比较

在Microsoft Visio Studio 6.0环境下进行仿真试验，列车自动运行系统ATO采用模糊预测控制算法，控制列车自动运行，综合考虑四大性能指标，根据其在列车不同运行阶段对ATO控车的不同影响，分别采用层次马氏距离法和模糊粗糙集法进行各性能指标的权重分配。不同方法的权重分配下ATO自动运行曲线如图3，图4所示。根据运行结果分析，2种方法均取得了不错的控制效果。

试验测试线路长1870 m，计划运行时间为165 s。层次马氏距离法分配权重后控制列车运行，其停车精度为0.11 m，运行时分误差为2.8 s。模糊粗糙集法分配权重后控制列车运行，其停车精度为－0.04 m，运行时分误差为－1.3 s，均满足相关规定(停车精确性指列车实际停车位置距离停车点±0.25 m之内，准时性指列车实际运行时间与计划运行时间的误差不超过2%)。相比较而言，模糊粗糙集法比层次马氏距离法得到的权重分配方法对ATO控车具有更好的控制效果。

5 结论

在分析了列车自动运行过程中不同的阶段准时性、停车精确性、节能性和舒适性等性能指标对列车运行的影响之后，学习性能指标权重分配方法。依据4个专家对3个运行阶段的四大性能指标重要程度离线打分，确定采用主客观方法相结合的层次马氏距离法，并依据列车实时运行过程中在不同档位下的四大性能指标值采用客观的模糊粗糙集法，来确定最终较客观的性能指标权重分配方案，促使ATO自动控车过程中控制策略的确定，最终取得了较好的控车效果。

性能指标权重在确定ATO控车策略过程中非常重要。本文虽采用了离线主客观结合和在线客观2种方法来对ATO控车过程中四大性能指标进行权重分析，但由于测试环境的局限性，不能应用到更多的线路和车型上，这也是有待进一步研究的方向，以探索更好的权重分配方法，使ATO更准确、高效、安全的自动控车。

［1］唐涛，黄良骥．列车自动驾驶系统控制算法综述［J］．铁道学报，2003，25(2):98－102.

［2］朱茵，孟志勇，阚叔愚．用层次分析法计算权重［J］．北京交通大学学报，1999，23(5):119－122.

［3］孙中央．列车牵引计算规程实用教程［M］．北京:中国铁道出版社，1999.

［4］王莲芬，许树柏．层次分析法引论［M］．北京:中国人民大学出版社，1990:8－18.

［5］黄定轩．基于客观信息熵的多因素权重分配法［J］．系统工程理论方法应用，2002，12(4):321－324