京沪线万吨列车主辅机最佳时间差仿真研究

麻冰玲

（沈阳铁路机械学校，辽宁沈阳110036）

随着京沪客运专线的建立，客货运输分线，提升京沪线货运能力已成为一个亟待解决的问题。使用大功率机车牵引万吨单编列车可以提高运能，但京沪线现有站台长度不能满足长大列车的停车要求。而大量的车站改造不仅投资巨大，而且耗时较长。而组合列车不仅可以解决停车问题，还可以提高运能，因此长大组合列车是提高京沪线运能的可行方式。长大多列车连挂运输使得列车的纵向冲动增加，因此多机车如何联合操纵、如何降低列车纵向冲动成为京沪线重载运输急需解决的问题。

大秦线重载运输已经开行2万t列车，已经完成多次2万t列车牵引试验和仿真研究［1-5］，但是大秦线使用牵引功率为9 600kW的HXD1和HXD2机车牵引，平均每台机车牵引质量达到10 000t。而在京沪线，因为现有站台条件限制，不具备开行单机牵引10 000t列车的条件。因此需要根据现有机车车辆配置采用两台机车牵引的编组方式，此外，京沪线使用车辆与大秦线也完全不同，大秦线使用特殊设计的C80车辆，由于车辆制动率与普通车辆不同，因此，大秦线的列车冲动特点和京沪线开行的10 000t组合列车有所不同，为了分析京沪线10 000t组合列车的纵向冲动情况，特选定大量使用的SS4型电力机车，普通线路上大量使用的C70车辆作为列车基本组成单元。

国外对重载列车仿真研究也比较活跃，意大利开展了短列车纵向动力学试验和仿真研究［6］，加拿大开展了数值仿真研究，给出了简单模型的计算结果［7］，伊朗通过模型研究制动传播对列车纵向冲动的影响［8］。

1 列车纵向冲动分析方法

列车纵向动力学分析时，将列车模型划为由一系列车辆组成，每个车辆模型划为一个集中质量，仅考虑每个质量块的纵向自由度，各质量块间由弹簧阻尼器连接。其中任意一个车辆受力如图1所示。

图1 单个车辆受力图

其中xi，vi，wi为i辆车瞬时位置、速度、重力。mi¨xi，FGi，FLi，FAi，FBi，Fci，Fwi分别为第i辆车瞬时惯性力、车钩力、牵引力或电制动力、运行阻力、制动力、曲线阻力、坡道阻力。

对每一节车辆，可以列出运动方程如下：

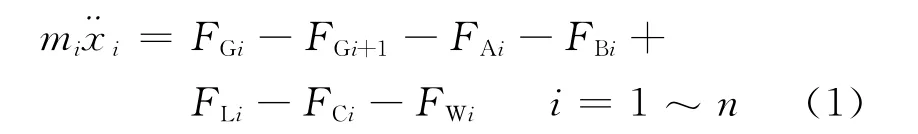
对于首、尾车辆：

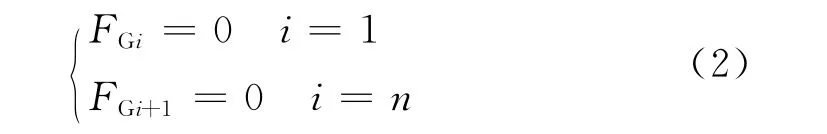
n为列车中机车车辆数总和。

车钩力FGi由每时刻计算出的两车相对速度和相对位移根据缓冲器特性计算；牵引力或电制动力FLi根据瞬时速度和选用机车的牵引力或电制动力特性曲线计算，牵引力取正值，电制动力取负值。没有牵引力和电制动力机车车辆FLi=0，运行阻力FAi根据车辆种类和载重状态根据牵规中［9］公式计算，空气制动力FBi由与纵向动力学同步计算的空气制动仿真系统计算出瞬时制动缸压力，再由每车制动倍率、制动缸直径等参数求出闸瓦压力，根据闸瓦压力求出摩擦系数，最终计算出瞬时空气制动力。曲线阻力根据牵规中［9］公式计算。坡道阻力等效于坡道千分数。根据上述方法计算出每一步列车加速度、速度、位移等物理参数，不断循环计算，直到指定的计算时间结束。

2 各种制动条件下车钩力

上述介绍的有大连交通大学开发的列车空气制动与纵向动力学联合仿真系统研究了10 000t列车双机编组组合列车，机车选用韶山4型（SS4）电力机车，C70型通用敞车为计算单元车辆。列车编组为1节机车+51节车辆+1节机车+52节车辆。重点研究常用制动、紧急制动、制动后缓解时车钩力分布情况。

2.1 常用制动车钩力分布特点（同步）

列车运行中，常用制动是使用最多的工况，所以有必要研究一下列车制动时的车钩力分布特点。计算了3种速度（50，70，90km／h），4种减压量（50，70，100，140kPa）常用制动工况下的车钩力分布特点。

图2是列车初速度为70km／h，减压量为70kPa制动过程中每车辆最大车钩力沿车长的分布曲线。图中横轴代表列车长度，纵轴为车钩力。正值表示拉钩力，负值表示压钩力。从图中可以看出，拉钩力曲线整体波动较小，基本都处于75～150kN范围内，最大值156.9kN出现在靠近列车中部的第42号车钩。压钩力基本呈鱼腹状分布，压钩力基本处于150～250kN范围内，第48号车钩出现了最大值255.2kN。

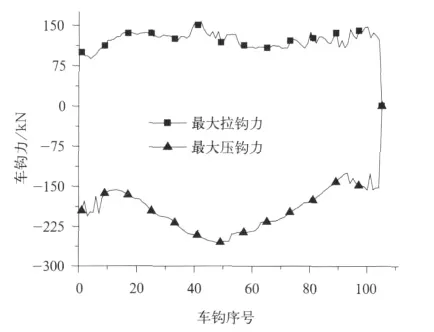
图2 速度为70km／h，减压量为70kPa时最大车钩力值沿车长方向分布曲线

图3绘制了制动初速度为90km／h时最大车钩力随制动减压量的变化曲线。图中所取的点是每种减压量时列车中最大压钩力和最大拉钩力。由图3看出随着列车减压量的增加，最大拉钩力和最大压钩力都呈现逐渐增大的趋势，以紧急制动时的车钩力为最大车钩力。紧急制动时最大拉钩力值为580kN，而最大压钩力值在640kN，压钩力略大于拉钩力。表1和表2分别列出了列车速度为90km／h时最大拉钩力和最大压钩力的数值及其变化情况。从这两个表可以看出，减压量相同时最大压钩力值大于最大拉钩力值。

图3 列车速度为90km／h时，最大车钩力随减压量的变化曲线

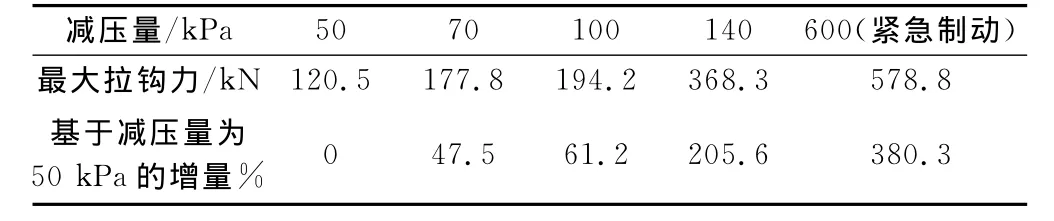
表1 90km／h时最大拉钩力随减压量的变化情况

2.2 常用制动后缓解车钩力分布特点（同步）

列车制动后缓解会产生很大的拉钩力，容易造成车钩断裂，因此研究制动后缓解车钩力就显得尤为重要。在列车初速度为50km／h减压140kPa制动后，当速度降为20km／h时，机车大闸由制动位转为缓解位，每个车辆车钩力沿列车长分布如图4所示。

由图4和图2的比较可见，缓解时拉钩力明显比制动时有所增加，这是因为具有很大惯性的列车前部制动力突然消除，而后部车辆仍有较大制动力。该拉伸力由前向后传播，逐渐增加，当传播到一定位置时，由于能量消耗，车钩力在某车辆处达到最大，图4的最大拉钩力值为747.6kN，发生在第61车位。

计算也发现最大压钩力值出现在制动的初始阶段，即制动过程影响着最大压钩力的产生。而缓解条件对列车的最大拉钩力影响很大。

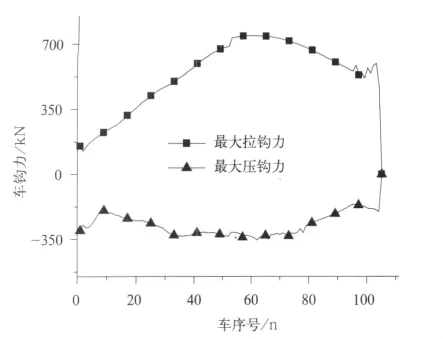
图4 速度50km／h，减压量140kPa，降速20km／h缓解时最大车钩力曲线

2.3 常用制动车钩力分布特点（不同步）

大秦线同步制动装置运用情况表明，即使是同步制动，主从机车也不可能真正的同步，因此有必要研究主从机车非同步动作对车钩力影响。

为研究主从机车不同步对车钩力的影响，分别仿真计算了初速度为50，70，90km／h，在各种不同减压量条件下，从控机车滞后于主控机车（简称“延迟”）和从控机车提前于主控机车（简称“提前”）的车钩力分布。图5绘出了列车速度为70km／h，减压量为70kPa时最大车钩力随主从控机车不同步时间的变化曲线。图中纵轴表示最大车钩力，横轴表示从控机车相对于主控机车的不同步动作情况，单位为s，负值表示从控机车提前，正值表示从控机车滞后，0点表示两机车同步动作。由图5可以看出从控机车滞后于主控机车动作时最大拉钩力和最大压钩力都明显增加，车钩力随着从控机车滞后时间的增加而增大。当从控机车提前于主控机车动作时，随着提前时间的增大最大压钩力逐渐趋近于一个恒定值，而最大拉钩力呈现了不断增大的趋势。综合分析拉钩力和压钩力，可以看出当从控机车提前时间为4s时车钩力具有最小值。为了了解主从机车不同步对制动距离的影响，绘制了相应工况下的列车制动距离曲线，如图6所示。可以看出，两机车同步动作时列车有最短的制动距离，但从控机车提前时间为4s，制动距离仅仅增加了不到30m，相对变化量仅为2.3%。由此得出结论，常用制动时，从控机车制动时间提前4s时，列车有最佳的纵向动力学性能。

2.4 常用制动后缓解车钩力分布特点（不同步）

主从机车不同步对列车缓解时车钩力也会有一定影响，图7绘出了列车初速度为90km／h，减压量为140 kPa，当列车速度降低为60km／h时缓解，最大车钩力随主从机车不同步时间的变化曲线。由图可知，从控机车延迟缓解时，最大拉钩力和最大压钩力随着延迟时间的增加都呈现了不断增大的态势。而对于从控机车提前动作于主控机车的情况，随着提前时间的增大最大拉钩力不断减小，最大压钩力减小后再增大，在4s时压钩力达到最小，因此从压钩力和拉钩力综合考虑，从控机车提前于主控机车4s为最优方案。

图5 速度为70km／h减压70kPa时主从机车非同步时间对最大车钩影响曲线

图6 速度70km／h，减压量70kPa主从机车不同步时间对制动距离影响

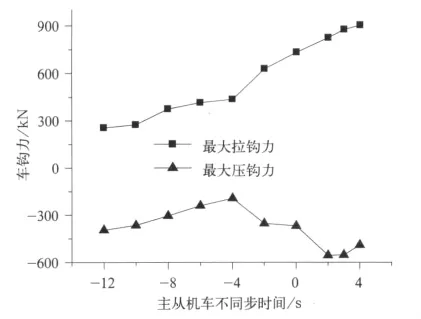
图7 速度60km／h缓解时最大车钩力随主从机车不同步时间的变化曲线

通过对其他工况的计算分析发现对于不同速度、不同减压量，“延迟”会大大增加列车的车钩力。而“提前”能够在一定程度上减小了车钩力，但是不同情况下，最优提前时间有所不同。

2.5 紧急制动时车钩力分布特点（不同步）

因为紧急制动具有较大的车钩力，并且对制动距离要求较高，因此分析紧急制动工况很有必要。

图8绘出了列车速度为90km／h，紧急制动时最大车钩力值随主从机车不同步时间的变化曲线。观察车钩力曲线容易看到，当从控机车滞后于主控机车动作时，最大车钩力（拉钩力和压钩力）明显地增加，而且随着延迟时间的增大车钩力值也越大。而时间“提前”使得车钩力有所减小，综合考虑拉钩力和压钩力，选择提前为1s时为最佳的列车操纵方案。

列车获得最佳纵向动力学性能是本研究所寻求的目标，但不能以牺牲制动效果为代价，图9显示了列车初速度为90km／h时，紧急制动时列车制动距离随主从控机车不同步时间的变化曲线。可以看出，当两机车同步动作时列车有最小的制动距离，虽然“提前”和“延迟”都使得列车的制动距离增大，但相对增加量都很小。提前1s时，相对于两机车同步动作的情况，列车的制动距离仅仅增加了不到1%。所以紧急制动的列车在制动效果基本不变的情况下，从控机车相对于前部机车提前1s动作列车有最优的纵向动力学性能。

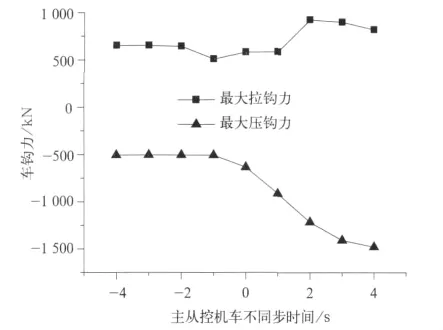
图8 速度90km／h紧急制动时最大车钩力随主从控机车不同步时间的变化曲线

图9 速度90km／h紧急制动时制动距离随主从机车不同步时间的变化曲线

3 结论

运用空气制动系统和纵向动力学系统联合仿真系统，计算分析了各种不同工况下制动以及制动后缓解、紧急制动情况下两机车同步动作时列车最大车钩力分布特点，以及相应工况下从控机车相对于主控机车动作时间提前或者延迟时最大车钩力分布特点。得出如下结论：

（1）列车常用制动时最大压钩力沿车长呈现鱼腹形状变化，最大压钩力值出现在中部位置；最大拉钩力曲线呈现了小量的波动，并无特别的规律。相同制动初速度情况下，随着制动减压量的增加，最大车钩力（包括拉钩力和压钩力）也不断增大。与常用制动相比，紧急制动时列车车钩力值最大。

（2）与列车常用制动相比，制动缓解时最大压钩力几乎保持了不变，而最大拉钩力却显著增加。制动过程主要影响着列车最大压钩力的产生，而缓解过程对列车的最大拉钩力影响很大。

（3）常用制动情况下，从控机车相对于主控机车制动延迟时列车的车钩力增大，且延迟时间越长车钩力越大。从控机车相对于主控机车制动提前使得列车最大车钩力减小，提前时间为4s时列车有最佳的纵向动力学性能，且列车的制动效果基本保持不变。

（4）制动缓解时，从控机车相对于主控机车动作延迟使得列车车钩力值增大，且延迟时间越长车钩力值越大。从控机车相对于主控机车提前动作可使得列车有更优的纵向动力学性能，最佳提前时间在4s左右。

（5）紧急制动时，在基本不影响列车制动效果的情况下，从控机车相对于主控机车提前1s动作，列车将获得最佳的纵向动力学性能。

（6）所有工况下，中部、头部两辆机车同步动作时列车有最小的制动距离，但从控机车相对于主控机车动作时间提前或延迟使得制动距离的增加量很小（最大增加量在5%以内）。

［1］耿志修.大秦线开行2万t重载组合列车系统集成与创新［J］.中国工程科学，2008，10（3）：31-43.

［2］高春明，冀 彬，张 波，等.大秦线重载组合列车的Locotrol技术应用研究［J］.电力机车与城轨车辆，2006，29（6）：5-7.

［3］常崇义，王成国，马大炜，等.两万吨组合列车纵向力计算研究［J］.铁道学报，2006，28（2）：89-94.

［4］魏 伟，赵连刚.两万吨列车纵向动力学性能预测.大连交通大学学报，2009，30（2）：39-43.

［5］赵连刚.基于制动系统仿真的两万吨列车纵向动力学分析［D］.大连交通大学，2008.

［6］P.Belforte，F.Cheli，G.DianaandS.Melzi，Numerical and experimental approach for the evaluation of severe longitudinal dynamics of heavy freight trains［J］，Vehicle Sys-tem Dynamics，2008，46，Supplement：937-955.

［7］M.Ansari，E.Esmailzadeh，D.Younesian，Longitudinal dynamics of freight trains［J］，International Journal of Heavy Vehicle Systems，2009.16，（1／2）：102-131.

［8］A Nasr and SMohammadi，The effects of train brake delay time on in-train forces［J］，Proc.IMechE.Part F：J.Rail and Rapid Transit，2010，224（6）：523-534.

［9］中华人民共和国铁道部.TB／T1407-1998列车牵引计算规程［S］.北京：中国标准出版社，1998.4-6.