一种提高N线模型探头标定精度的解算方法

朱立人 李文骏 丁 辉 王广志

(清华大学医学院生物医学工程系，北京 100084)

引言

超声成像技术由于其本身的诸多优点，被广泛应用在临床诊断和介入手术引导等医学领域。尤其是与X线透视成像、计算机断层成像(CT)、磁共振成像(MRI)等其他医学成像手段相比，超声影像因为没有电离辐射、在成像时间方面没有限制，并能为医生提供病人实时的影像信息，因此在引导介入手术中起到了十分重要的作用［1－2］。

在超声引导介入治疗和手术中，超声探头的空间位置需要通过三维空间定位系统进行跟踪，并且与同时被跟踪的手术器械等统一到同一个坐标系中，以便将器械姿态和位置准确地显示在超声图像上，呈现给医生。利用三维定位系统跟踪超声探头的技术，同样被应用于徒手(free-hand)三维超声图像的获取［3］。为了能够跟踪超声探头，以及探头上延伸出的成像平面，首先必须确定从位置跟踪传感器坐标系到超声成像平面坐标系之间的变换关系。测量和解算这个变换的过程就是超声探头标定，这个过程中基本的坐标系变换关系如图1所示。

目前，人们已经提出若干种模型和方法来实现超声探头与定位系统传感器的标定［4］，其中最为广泛应用的方法之一是 N线模型方法［5－6］。这种模型在水箱中设置许多由尼龙线组成的N形目标。当超声平面切过这些N形目标时，每个N形靶线在图像上产生3个亮斑。手动识别和拾取三个亮斑的坐标后，通过左右2个亮斑到中间亮斑的距离之比，并结合模型的设计约束，可以重建出N形目标与成像平面交点在设计坐标系中的3D坐标值。通过同一个目标在超声图像坐标系和位置传感器坐标系中的测量，即可解算出标定变换关系。传统的解算方法包括解析的［7－10］和迭代的［11］最小二乘算法。

图1 超声探头标定的物理模型Fig.1 physical model of ultrasound probe calibration

然而，由于超声探头的声场随着深度增加而扩散，超声成像面并非理想的几何平面。有一定厚度的成像面与线形目标相交，反射目标在理想成像平面上的投影并不是一个点，从而形成线状甚至弧形的亮斑，如图2所示。这样的光斑在手工或者自动拾取标志点坐标时存在很大的误差和不确定性，引起N形目标三维坐标重建计算中的误差增大，导致这个过程中原本存在的共面性丢失，进而引起最小二乘准则下的解算精度下降。

针对传统基于N线模型超声探头标定算法中重建获得目标点三维坐标共面性丢失的问题，本研究设计了一种解算方法，在不改变目前标定流程的基础上，通过拟合平面的方式重塑共面性，提高探头标定的精度。

图2 N线模型的超声图像Fig.2 typical ultrasound image of N-phantom

1 标定原理

1.1 N线模型标志点重建

用于超声探头标定的N线模型通常由多层尼龙线安装在水槽中组成，每一层的尼龙线穿成若干如大写英文字母N形状的靶线，如图3所示。图中将模型正面板部分打开后，显示了2层N形靶线，其中作为目标的斜线用虚线表示。每一个N形靶线中的斜线(图中虚线所示)与超声成像平面相交的交点成为求解配准变换关系的标志点，交点在二维超声图像上的位置容易通过手动拾取的方式获得。通过靶线设计形状的约束，则可以重建出这些交点在三维模型中的位置。

图3 N线模型设计Fig.3 diagram of N-phantom design

对于模型中的任意一个N形靶线，图4示意了它与有一定厚度的超声成像平面相交的情况。在理想的情况下，超声成像面为空间中的几何平面，并与靶线相交于E、F、G等3点。在超声图像中，可以直接拾取N形靶线中的目标点E、F、G。同时，通过图像中线段EF与FG长度的比值以及AC、AB的设计尺寸，由ΔBEF和ΔCGF的相似关系，即可计算出F点在BC约束线段上的位置，进而得到F点在模型坐标系下xm和ym轴的坐标值;根据该N形靶线所在的层数，知道它的深度坐标zm。计算N形靶线中的目标点F在模型坐标系下三维位置的过程，将其称为目标点的“重建”。重建后，将会得到一系列目标点对。在理想情况下，这些点将在三维坐标系中构成一个平面。

图4 N形靶线目标点重建原理Fig.4 target point reconstruction in N shaped fiducials

然而，在实际情况下，超声平面与靶线相交，形成3个在横向(xi轴方向)上有一定长度的扩散亮斑，无法很准确地选取交点。这不但降低在超声图像中拾取注册用标志点的准确性，而且由于F点在模型坐标系中的重建过程对EF和FG长度的比值敏感，还会导致重建得到的F点在模型坐标系下坐标不精确，丢失目标点集在三维模型坐标系中的共面性。

1.2 数据采集与预处理

在标定过程中，用于采集标定数据的实验系统一般涉及到图5所示的坐标系和空间变换关系，其中待标定的变换是 Ts←i。为了计算这个变换，需要获得图像坐标系和传感器坐标系下的一组对应点的坐标数据。为此，首先要计算从模型坐标系xmym－zm到固定在定位系统上的“世界坐标系”xwyw－zw的变换关系 Tw←m。通过可被空间定位系统跟踪的探针，点选出模型外壁和上缘的定位小孔，并将小孔在世界坐标系中的位置和在模型坐标系中的位置配准，就可以计算出这个变换关系Tw←m。

接着，用超声探头获得模型一个切面的图像。得到图像后，首先是对任意一个N形靶线拾取其在图像上的点，如图4所示的 E、F、G等 3点。一方面，将其中目标点F的坐标扩展为三维，得到超声图像上的配准点集;另一方面，通过前述方法，重建这些由标志点F对应的模型坐标系三维坐标。通过上一步计算得到的变换关系，以及定位系统获得的从世界坐标系到传感器坐标系的变换，可以将重建得到的点变换到传感器坐标系下，即

通过上述过程完成数据采集和预处理的坐标变换之后，就可以解算超声探头与定位系统传感器之间的标定变换。

2 解算方法

2.1 解算方法概述

至此，可获得所有N形目标中靶线与成像平面交点的传感器坐标系的坐标和超声图像坐标系的坐标，两组坐标之间的基本变换关系为

式中，R为旋转矩阵，t为平移向量。

这就将标定问题抽象为一个已知配对关系的基于标志点的刚性配准问题，而传统的标定解算方法是使用最小二乘配准准则进行解算。在这种理论上发展出了许多配准算法，都可以应用于标定问题的求解，如应用较广的解析求解方法［9］。最小二乘算法依赖于高斯随机噪声假设，而前述重建过程失去共面性的问题属于系统误差，各点之间的误差存在相关性。因此，最小二乘算法获得的结果虽然最优化了参与计算的注册点误差(fiducial registration error，FRE)，却可能有较大的目标注册误差(target registration error，TRE)。

针对传统解算方法的这个问题，笔者提出如下改进方法:首先通过拟合重建这些目标点的共面性，然后在平面内应用最小二乘配准方法获得标定结果。

2.2 重建平面

为了重建传感器坐标系下配准点的共面约束，首先使用这些点拟合一个平面。三维空间中的平面可表示为

式中，平面的法向量为 n= ［a，b，c］T，于是空间中任一点 x= ［x，y，z］T到该平面的距离为

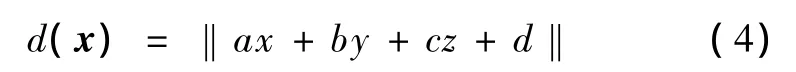
期望所有传感器坐标系下的观测点到该平面的距离之和最短，即求解约束优化问题，有

由于该问题是一个带二次约束的非线性规划问题，优化方法使用逐步二次规划法(sequential quadratic programming，SQP)，而初值可以用观测点集中的任意3个点估计。

在获得拟合的平面之后，将传感器坐标系下的原始观测点(即通过重建得到的标志点三维坐标{})投影到拟合平面上，作为新的注册点集。投影点的计算方法为

2.3 共面约束下的配准

步骤1:去中心。求解所有N组点对在两个坐标系下的质心，并将两组点平移到质心重合。

步骤2:求解两个平面之间的旋转。变换前后的两个平面法向量容易求出，分别记为nw、nm，所求转轴即为两个法向量的叉积。而转动的角度满足cosφ =nw·nm，sinφ = ‖nw× nm‖。记这一步旋转对应的旋转矩阵为Ra。

步骤3:求解平面内的旋转。定义

转角满足如下关系

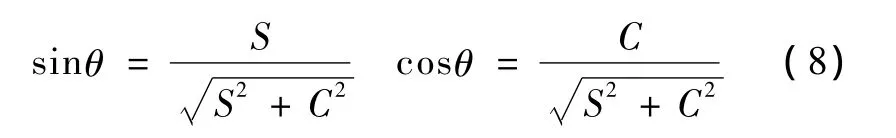
这个变换的转轴为nm，这一步得到的旋转矩阵记为 Rb。

步骤4:得到结果。最优旋转矩阵Ropt和最优平移分量topt分别为

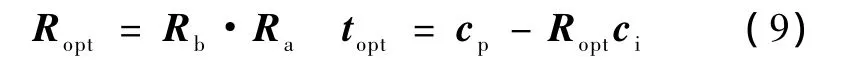
通过上述步骤，求出旋转矩阵和平移向量一同构成的标定变换，其齐次变换矩阵为

3 精度验证实验与结果

3.1 实验方法

为了验证新的解算方法的精度，使用自行设计的N线模型进行了实际标定实验验证。该模型使用有机玻璃制造，长宽高尺寸为28 cm ×11 cm ×24 cm;模型外壁和上缘分布了多个位置精确的小孔，作为该模型自身空间位置的定位孔。模型内部分布了7层深度为4～16 cm的靶线，由尼龙线穿成，每层有4个N字母形状的目标，共28个。

在本研究中，采集系统包括:超声成像设备(DC-6，迈瑞医疗)配临床常用的3.5 MHz腹部探头、交流脉冲电磁三维定位系统(Aurora，Northern Digital Inc)、PC工作站(xw8400，HP)。超声影像以模拟信号方式输出，在PC端由视频采集卡对超声影像进行数字化;通过 RS-232串口，将同步测量的探头空间定位系统数据发送到PC端。标定在室温下进行，标定时向模型中注入去除气泡的纯净水。由于标定的结果需要应用于人体组织的成像和测量，而声速在人体组织和纯水中并不相同，因此在图像采集过程中，可使用超声设备自带的液性声速补偿功能，以减少扫描线方向距离测量误差。

在实验中，对于同一个待求解的超声影像与定位传感器之间的变换关系，在模型上取7个不同位置，采集得到7幅可用于标定的图像。在实验中，选取的超声成像深度为17.5 cm。由于成像位置不同，在7幅超声图像上可识别并用于标定的N形靶线数目略有不同，分别为 13、11、10、9、14、5、6，共 68个标志点。

3.2 精度验证结果

对解算方法精度的验证分为两个方面:共面性和配准准确度。前者是为了论证在解算过程中重建共面性的必要性，后者是为了验证所提出方法在实际标定中的精度。

在共面性验证中，将从超声图像中重建得到模型坐标系点集，分别用前述的拟合方法估计一个虚拟的成像平面，并计算每幅图像中的各个标志点与虚拟成像平面之间的距离。得到结果如表1所示。可以看到，部分图像上(1、2、4号)的共面性偏离最远处可以超过1 cm。因此，若不进行共面性约束面直接利用传统最小二乘解算方法来计算标定矩阵，显然会导致较大误差。

为了验证配准准确度，将共面性验证中得到的每幅图像上距离虚拟成像平面最近的点保留作为目标点，分别用传统解算方法和所提出的方法对标定变换进行解算，计算并比较两个标定变换下目标点的配准误差(TRE)。TRE可定义为

验证结果如表2所示，表明新的解算方法的TRE均比传统解算方法的TRE要小。传统方法的TRE均值为5.88 mm，而所提出方法的TRE均值为4.11 mm。如果将误差明显较大的2号标定图像排除(可能存在明显的标志点选取异常)，两者的精度均值分别变为1.50和1.19 mm，依然有较为显著的精度提高。

表1 标志点三维坐标到拟合平面的距离统计Tab.1 The statistical result of the distance from 3D fiducial markers to the fitted plane

表2 目标注册误差(TRE)比较Tab.2 Comparison of target registration error(TRE)

3.3 共面性与波束

由于重建后标志点的共面性与波束随成像深度的变化有关，因此研究共面性指标在不同深度上的变化，有验证本研究假设的意义。

将实验数据中标志点到其对应的拟合平面的距离按其在平面两侧给定符号，构成有向距离。接着，将标志点按照其所在的成像深度(超声图像上y方向的坐标值)排序。由于标志点集中在深度0～160 mm的深度区间内，因此按照0～30、30～60、60～90、90～120、120以上共5个区间，统计有向距离的标准差。落在各个区间内的标志点数目分别为5、8、16、18、20，这能够较可靠地统计各个深度的标志点重建之后的散布情况。标志点有向距离随深度变化的散点情况和标准差统计情况如图6所示。

4 讨论

将本研究得到的标定准确度与Pagoulatos等的结果［5］进行比较，在本研究的实验系统上，传统方法的标定误差5.88 mm比报道的3.14 mm的误差要大一些。由于两者的标定方法和验证方法在理论上基本一致，这可能是由于所使用的定位系统、成像设备性能上的差异而造成的。使用笔者提出的新解算方法后，标定误差降低到4.11 mm。在设备性能落后的情况下，达到与其相近的准确度。罗杨宇等未报道其使用的超声设备和定位系统的具体型号，但所得到的标定误差4.80 mm与本方法得到的标定误差接近［6］。

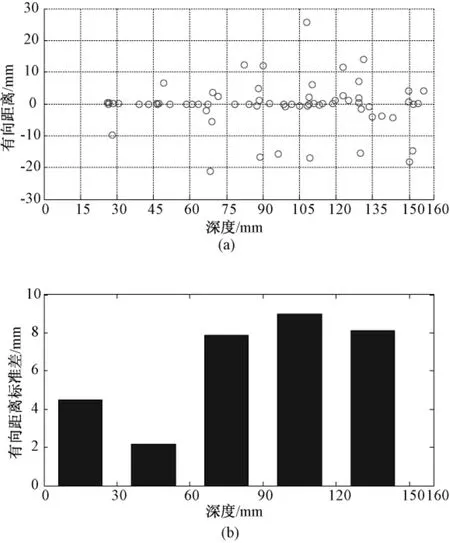
图6 共面性指标随成像深度的变化。(a)标志点有向距离分布;(b)不同深度有向距离标准差Fig.6 Variance of indicator of planarity as depth changes.(a)distribution of signed distance of fiducials;(b)Standard deviation of signed distance

将表2中的标定误差与表1中的共面性指标相对照。对于共面性较差的图像，新的解算方法在配准误差上的改进更为明显。比如，对于偏移虚拟成像平面超过1 cm的3组数据(图像编号为1、2、4)，本方法相对于传统解算方法的改进达到10%。这说明，在能观察到较为明显的共面性丢失时，新的方法确实能够起到较好的提高标定精度的作用;而当共面性丢失不明显时，新的解算方法能稳定地得到与原方法可比的标定结果。

N线模型标定过程中，标志点共面性的丢失，本质上是由于超声波束在传播过程中形状逐渐发散而引起的。关于波束宽度问题，Prager等在1998年就有提出［3］，在医学超声成像的专著［12］中也进行了定性描述。Chen等定量测量了超声探头用于成像的波束宽度随着成像深度的变化，使用了频率较高的探头(13～16 MHz)，波束在较浅的焦点处变窄，然后逐渐变宽［13］。图6显示了在本研究实验中得到的N线模型标志点在拟合平面两侧的分布情况，而有向距离的标准差表征了点在平面两侧的散布。可以看到，共面性在30～60 mm之间是最好的，过深或过浅时都有所下降，在超过120 mm之后又稍有提高。这个结果与在超声设备上设置了的5和15 cm两个电子聚焦焦点有关，同时也与文献［13］中得到的波束先聚合再扩散的实测趋势吻合，证明了共面性丢失与波束宽度和形状变化有关。

5 结论

对于超声引导介入手术等应用，利用三维空间定位系统跟踪超声成像平面位置与姿态是重要的环节，标定超声探头与定位系统传感器之间的变换关系则是实现跟踪的基础。针对目前广泛使用的N线模型方法，在讨论传统解算方法中重建的三维坐标失去共面性的问题及其对精度影响的基础上，本研究提出一种通过重塑共面性、提高解算精度的方法。实际标定实验验证了所讨论的共面性失去问题，与传统解算方法相比，新的解算方法在标定精度上可以得到提高。

［1］Xu S，Krucker J，Turkbey B，et al.Real-time MRI-TRUS fusion for guidance of targeted prostate biopsies［J］.Computer Aided Surgery，2008，13(5):255－264.

［2］Solberg O，Lango T，Tangen G，et al.Navigated ultrasound in laparoscopic surgery［J］.Minimally Invasive Therapy＆ Aided Technologies，2009，18(1):36 －53.

［3］Prager R，Rohling R，Gee A，et al.Rapid calibration for 3-D freehand ultrasound systems［J］.Ultrasound in Medicine ＆Biology，1998，24(6):855－869.

［4］Mercier L，Lango T，Lindseth F，et al.A review of calibration techniques for freehand 3-D ultrasound systems［J］.Ultrasound in Medicine＆ Biology，2005，31(2):143－165.

［5］Pagoulatos N，Haynor D，Kim Y.A fast calibration method for 3-D tracking of ultrasound images using a spatial localizer［J］.Ultrasound in Medicine＆ Biology，2001，27(9):1219－1229.

［6］罗杨宇，徐静，鲁通，等.基于磁定位器的手动三维超声图像标定［J］.中国生物医学工程学报，2008，27(2):250－254.

［7］Schonemann PH.A generalized solution ofthe orthogonal procrustes problem［J］.Psychometrika，1966，31(1):1 －10.

［8］Horn BKP.Closed-form solution of absolute orientation using unit quaternion［J］.J Opt Soc Am A，1987，4(4):629－642.

［9］Horn BKP，Hilden HM，Negahdaripour S.Closed-form solution of absolute orientation using orthonormal matrices［J］.J Opt Soc Am A，1988，5(7):1127－1135.

［10］Arun KS，Huang TS，Blostein SD.Least-square fitting of two 3-D point sets［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，1987，PAMI-9(5):698 －700.

［11］More J.The Levenberg-Marquardt algorithm:implementation and theory［C］ //Watson G，eds.Numerical Analysis.Berlin:Springer，1978:105 － 116.

［12］高上凯.医学成像系统［M］.(第2版).北京:清华大学出版社，2010:115－119.

［13］Chen TK，Thurston AD，Moghari MH，et al. A real-timeultrasound calibration system with automatic accuracy control and incorporation of ultrasound section thickness［C］ //Miga MI Cleary KR eds. Proc. of SPIE.Bellingham:SPIE，2008:69182A－1－69182A－11