基于二维和三维分形分析技术的直肠癌患处局部血流空间异质性测量流程的结果再现性评估
Bal Sanghera, PhD Debasish Banerjee, FRCR Aftab Khan, MRCS Ian Simcock, MSc
J. James Stirling, MSc1a Rob Glynne-Jones, MD, FRCR1b Vicky Goh, MD, FRCR1a,2
分形现象可被描述为一种“自相似”结构,即整体结构的每一部分在更小的尺度下都与原始结构相似。自相似结构以非整数维度的形式存在,并难以用欧几里得几何学形容。
分形分析提供了一种评估肿瘤血管空间结构的方法[1-5]。不同的分形参数,诸如分形维数(目标对象填充空间的方式),分形丰度(填充空间的程度)和缺项性(目标对象内部结构的异质性程度)等,可以从不同角度展示肿瘤血管网的空间形态,进而展示了血管网分布的的空间异质性。当与动态对比增强技术联用时,分形分析技术将可以为肿瘤血管分布标准量度(如传输常数和局部血流量[1-5])提供补充,特别是在评估治疗效果等血管网可能发生异质性变化的情况下[6-7]。截止本文撰写时,动态对比增强技术已应用于二维分形分析过程。最近,三维动态对比增强数据的获取使三维分形分析成为可能。通过对整个肿瘤的轮廓进行分析,三维分形分析或能够更加综合地评估肿瘤的分形属性。结果再现性(或者多次检验结果的一致性)是临床应用一个很重要的参数,分形分析技术可以在一定程度上改进这项参数。本研究的目的是,通过盒子计数方法描绘直肠癌患部血流状况(数据由容积螺旋CT灌注成像测量所得)的二维和三维分形属性,并确定结果的再现性。
1 材料与方法
1.1 患者
本研究获得制度审查委员会批准和患者的知情同意。本研究中,所涉及的患者均为刚刚被诊断出直肠癌的成年患者。根据灌注CT的筛选标准排除肾脏有损伤(血清肌酸酐水平>120 μmol/L或肾小球滤过率<50 mL/min)的、之前有碘化造影剂过敏反应的、无法执行静脉穿刺置管术的和在成像结果中无法鉴定肿瘤的患者。在2009年5月到2010年9月间,有10位患者(平均年龄72.3岁;年龄范围52.1~79.7岁),包括8位男性(平均年龄68.8岁;范围52.1~79.7岁)和2位女性(平均年龄75.7岁;范围73.0~78.4岁),在没有接受介入治疗的情况下,于24 h内接受了2次容积螺旋CT灌注成像研究以确定治疗前的基线信号再现性(重复检验结果的一致性)。此外,研究人员还通过标准的磁共振(MR)成像流程检验肿瘤的分期与尺寸。此次研究所招募的患者均通过了灌注CT的准入筛查。
1.2 容积螺旋灌注CT成像
研究人员用四维适配螺旋模式对所有患者进行了容积螺旋灌注CT成像(Somatom Definition; 西门子医疗,福希海姆,德国)检查,该四维适配螺旋模式能够获取头-尾向和尾-头向的图像。患者检查结果包括一幅“解剖结构图”,一帧定位已知肿瘤的小剂量非增强螺旋CT成像(80 kV;70 mAs[有效]; 旋转时间0.5 s;检测器数目:24;截面厚度1.2 mm;倾斜度1.2;层面准直5 mm;扫描视场300~450 mm;扫描像素尺寸512 mm),以及一幅容积螺旋动态对比增强CT成像。在进行对比增强成像过程之前,研究人员以6 mL/s的速度向病人体内先后静脉注射50 mL碘化造影剂(碘佛醇,每毫升含350 mg碘)和50 mL生理盐水。
从开始注射对比材料到开始容积螺旋动态对比增强CT成像过程,中间有10 s的延迟时间。容积灌注螺旋CT成像采用的是四维适配螺旋模式,并在最初的30 s将扫描周期设为1.5 s,在之后螺旋成像的20 s,将扫描周期修订为3.0 s并调整以下参数:100 kV;110 mAs;z轴覆盖范围11.4 cm;扫描视场300~450 mm;扫描像素尺寸512 mm;容积CT放射剂量,116.04 mGy。研究人员将图像重建至3 mm截面厚度,比原始图像增加了2 mm。
1.3 图像分析
1.3.1 CT成像分析
CT图像的处理是由一位放射科医师(V.G.,具有10年以上灌注CT分析经验)完成的。处理图像时,该医师将CT数据载入到一台标准图像处理工作站(MMWP;西门子医疗)使用基于反卷积算法的容积灌注CT处理技术(VPCT, Version 1.0;西门子医疗)对图像进行处理。最初的后置处理包括运动校正,设置使用四维噪音过滤器,数据处理的临界值(-50~200 HU)选择,以及通过在股动脉或外部髂骨动脉中设置圆型感兴趣区域来绘制动脉信号随时间的衰减曲线。研究人员导出局部血流量参数图(单位为mL/min/100 mL,每个像素代表1个参数值),包含整个肿瘤在轴向、冠状和矢状平面(图1)中的数据,以备分形分析所用。

图1 同一等级的T3N1型直肠肿瘤在(a)轴向,(b)冠状,(c)矢状平面上的典型局部血流量示意图
1.3.2 分形分析
为了将肿瘤区域与周围组织相区分,2位放射科医师(D.B.和V.G., 均有10年以上放射科工作经验)用专业软件(ImageJ;国立卫生研究院,贝塞斯达,马里兰州)对整个肿瘤的参数灌注图做了进一步的处理。信号强度阈值被设定为35~100 mL/min/100 mL,以获取肿瘤区域的图像(参照先前的研究[5])(图2)。获取肿瘤区域图像后,课题组的研究人员使用自己编写的分形分析软件对上述图像进行二维和三维的计盒法分形分析,该分析过程主要涉及以下分形参数:(a)分形维数,代表一个物体填充空间的方式;(b)分形丰度,代表已占空间的体积;(c)缺顶性,反映物体结构的不均匀程度[8-9]。研究人员使用二维平方和三维立方计盒法,从所有可能作为盒子起始点的空间节点出发,以下列公式计算出分形维数和分形丰度:NL=KL-D,其中L为盒子尺寸,NL为为覆盖目标区域而需要的尺寸为L的盒子的数目,D为分形维数。通过在指数坐标系中绘制NL对L的关系图,可由直线部分的斜率得出分形维数,还能由曲线的直线部分的y轴截距中求得分形丰度(logK)。该分析过程使用已知分形维数的简单结构和复合结构(如多次迭代的二维和三维Sierpinski分形结构)。

图2 (a)灌注CT成像和 (b)直肠肿瘤从周围组织分割衍生的合成影像
研究人员使用二维和改进的三维滑块法[9]计算缺项值,该法由下列公式定义:
□=(∑s2s2Q(s,r))/[∑sQ(s,r)]2
其中□代表缺顶,r代表盒子的尺寸,s代表被某一特定尺寸盒子所占据的位点数量,Q为概率分布(该指数为某一特定体积r的盒子所占据的空间位点数量除以体积为r的所有盒子的总数)。在指数坐标系中将缺项系数与计数盒子的体积的相关关系作图,可以获得缺项性的详细信息。
为确定二维、三维分形分析和缺顶分析的结果再现性,本研究在24 h内请上述两位放射科医师用同样方法重复了整个过程,所处理的数据为在24 h内通过同样的成像和运行参数所获取的容积灌注CT成像结果。
1.4 统计学分析
研究人员求出了分形维数和分形丰度的平均值±标准差,通过配对t试验对二维和三维的分形参数进行比较,统计显著性在5%。
研究人员用Bland-Altman统计[10]对分析结果再现性进行评估,并计算了结果的平均差和结果95%一致的数据分布范围(平均差-2,标准差和平均差+2,标准差之间的范围)。患者之间的差异系数的计算方法如下所示:首先计算出数据数值间的部分差异,并算出标准差相对于平均值的百分比例。然后,研究人员使用均方根法对同一患者两组数据间的差异系数进行评估:(SD/M)2(其中SD为标准差,M为平均值),并求出不同患者的该项数值的平均值和平方根对于平均值的百分比例。方差组分分析通过混合效应模型方法实现,在该分析中,研究人员对每位病人设定一个特定的编号ID,并用混合效应模型计算的结局和斜率(测量时间)来衡量随机效果(测量数据=截距|ID+斜率•时间|ID)。两位观测者之间的数据一致性评估是通过使用Bland-Altman统计方法计算二者的平均差和95%一致性范围来实现的。上述统计学分析步骤均用软件(Stata,9.0版;Stata, College Station,德克萨斯州)完成。
2 结果
肿瘤的特征与分期的数据见表1。平均肿瘤尺寸(5.03±1.04)cm (标准差)。灌注生成的血流量图谱展示了二维和三维图像的分形属性。在第一次和第二次扫描中,在对数坐标系中,分形维数估值NL与虚拟盒子尺寸L的散点线性回归r2值均为0.99或者更高。来自两位放射科医师的其中一位的数据显示,三维分析的分形维数和分形丰度高于二维分析的相应数据(分形维数[P<0.0001]的平均值2.488比1.648),这和预期的情况相符。上述结果中很重要的一点是,在对于两轮成像的三维和二维结果进行分形维数 (图3)和分形丰度(图4)进行比对后,研究人员发现两轮成像结果的分析结果之间存在良好的一致性(表2)。二维分析的差异系数高于三维分析,但也保持在7.35%以下。缺项性方面,第一、第二次成像结果的二维和三维缺顶值-虚拟盒子尺寸关系图也直观地表现出不同数据系列缺项属性的相似性(图5)。方差分量分析结果显示,患者之间的差异程度高于三维和二维分形分析变量之间的差异程度(表3)。

图3 (a)散点图和(b)对读数1重复研究的二维和三维分形分析的分形维数的Bland-Altman平面图

表1 肿瘤特征与分期数据

表2 第一和第二次研究中读数1二维、三维分析下分形维数和丰度的再现性
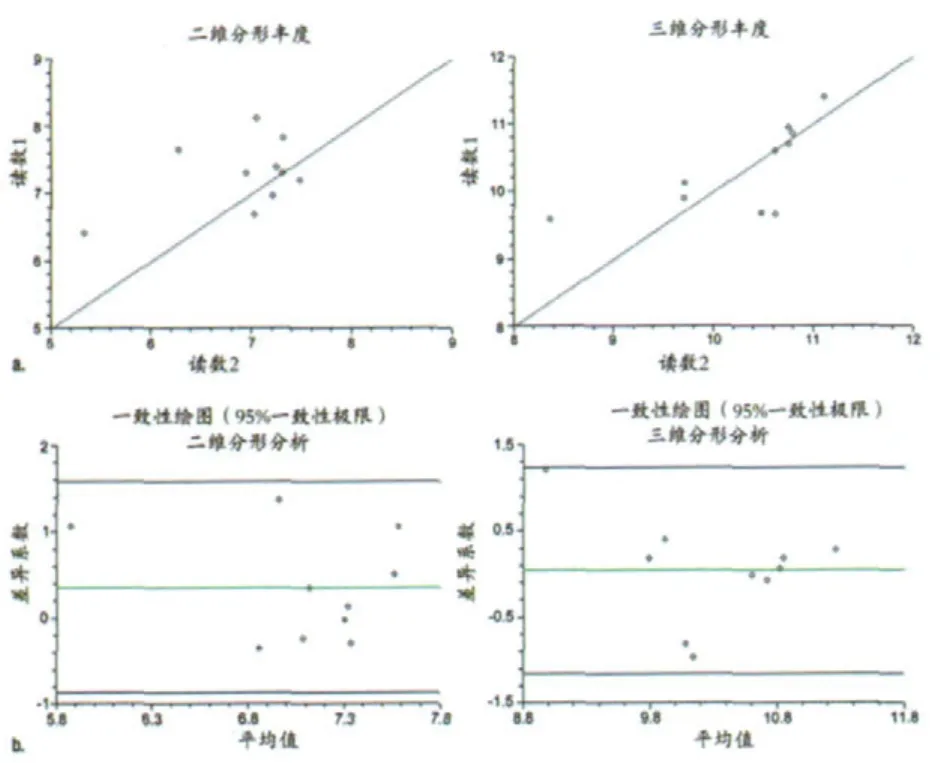
图4 (a)散点图和(b)对读数1重复研究的二维和三维分形分析的分形维数的Bland-Altman平面图
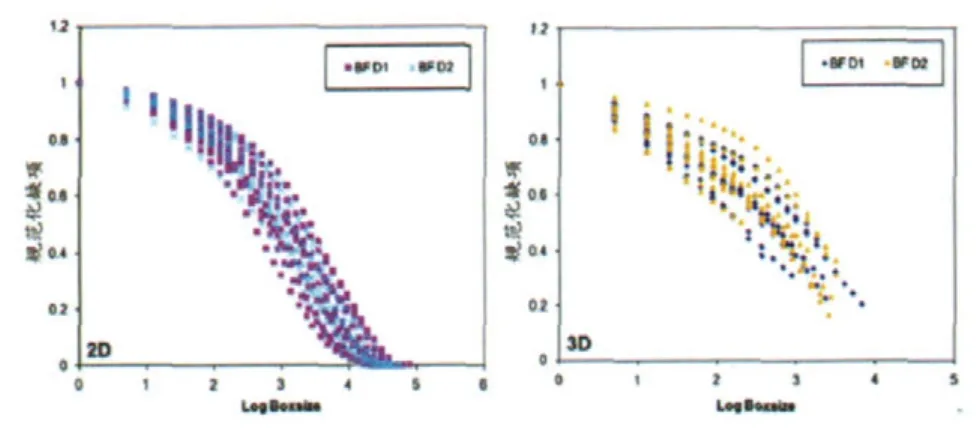
图5 读数1的 (a)二维和(b)三维分形分析的规范化缺项平面图。BFD1=第一次研究中的血流量,BFD2=第二次研究中的血流量。

表3 第一次研究中读数1、2二维和三维分析分形维数和丰度的通用一致性
来自两位放射科医师的第一轮成像数据分析结果也表现出了良好的一致性,其中Bland-Altman图表明,二维和三维分析的分形维数的平均差分别为0.030(95%一致性极限: -0.143,0.204)和0.014(95%一致性极限: -0.018,0.0472),二维和三维分析的分形丰度分别为-0.073(95%一致性极限: -0.823,0.676)和-0.044(95%一致性极限 :-0.139,0.052)。
3 讨论
空间异质性是具有生物学意义的肿瘤表现出的一项重要属性。在肿瘤中通常难以维持正常的血管分支系统[11],而是在有的区域血管分支密度增加,而有的区域减少。新生血管同样会具有不同的外膜细胞覆盖程度,从而在功能成熟度[12]表现出差异,这导致不同区域间的灌注差异。灌注不足区域会显示出更高的缺氧程度,其空间分布也会随时间推进呈现出功能和结构上的变化[13]。目前的定量动态对比增强成像分析方法还不能清晰地描绘血管分布的空间异质性程度。
组织学研究显示,分形分析能够更好地描绘血管系统分布的随机性,这是微血管密度测量[14]等常规方法所不能做到的,而且分形分析作为成像后处理方法还有提高现有成像技术所得结果[1,15-18]的潜力。动态对比增强磁共振成像研究已经运用不同的分形方法[1-4]评估肿瘤的分形属性,用以评价神经胶质瘤的分级[2]以及肝转移瘤[1]和软组织恶性肿瘤对苯丙氨酸氮芥和肿瘤坏死因子的α[3]的治疗反应。与动态对比增强CT相似,二维分形分析的结果证实,直肠肿瘤部位的分形属性(维数和丰度)与正常的直肠之间存在显著差异[5]。然而二维分形分析亦有其局限性:二维图像由于分形尺度不能无限的变化,因而无法完美展示目标的分形属性。通常情况下,对于肿瘤的二维分形分析通常涉及一个或几个连续的轴向切面图像,从而难以完全覆盖整个肿瘤区域的三维信息。基于上述原因,临床上需要针对肿瘤的三维分形分析技术。本文的结果证实,和先前估计的情况相符,二维和三维分形技术在分形维数、分形丰度以及缺项性上均有区别,而且三维分形分析结果中的各项数据均更关键。
本研究实施的两轮CT扫描所获得的数据的二维和三维分形分析结果均体现出良好的组间一致性,二维分形分析结果的变异系数更高。本研究中,我们推测该现象与分割肿瘤图像的操作有关。在三维分析中,通过处理一系列连续轴向图像,研究人员可以更轻松地辨别肿瘤边缘并将肿瘤区域从相邻的非肿瘤组织中区分出来,这比二维分形分析中处理单一横断面图像更容易。
分形分析是一项很有前途的图形处理工具,但是还有许多问题需要考虑。市面上已经存在许多分形软件技术可以使用[19]。通常情况下,这些软件均是研究人员自行开发的科研用工具软件,采用三维网格空间计盒法进行分形分析操作。分形维数参数的分析结果会受到计盒法起始点位置的影响,而将所有可能的计盒起始点纳入到计算过程中可以减小这种影响。本文中,分形分析结果的线性回归适应值(r2)高于0.99,这也证实了肿瘤血管结构在二维和三维空间中的分形行为。参与此次研究的患者很少,为获得再现性数据而进行的重复研究的电离辐射(有效剂量可达40 mSv)造成的伦理挑战依然存在。
在本研究中,研究人员仅使用了分形分析,因为本研究的目的是用分形分析法测试容积灌注螺旋CT成像获取的直肠恶性肿瘤局部血流的二维和三维分形属性,并确定结果再现性。如何将分形分析的结果与其他异质性分析手段相比较,如柱状图分析和纹理分析,是将来可能的研究方向。
总之,灌注CT得出的直肠肿瘤血流分布呈现了二维和三维的分形属性。使用计盒法和缺项性评估的分形分析技术在本研究中体现出了良好的组间一致性。二维分形分析的变异系数高于三维分析,因为其覆盖的肿瘤体积较小,这说明三维分形分析是一种更为可靠的测量方法。做为一种空间异质性的评测方法,二维和三维分形和缺项分析在CT定量检测直肠肿瘤方面具有较高的研究和开发价值。
知识补充:
(1)灌注CT导出的直肠癌局部血流量证明了二维(2D)和三维(3D)分形分析的分形属性。
(2)平均的二维分形维数和分形丰度分别为:1号放射科医师,1.648±0.09(标准偏差)和7.278±0.51;2号放射科医师,1.617±0.08和7.351±0.47;平均的三维分形维数和分形丰度分别为:1号放射科医师,2.488±0.09和10.338±0.64;2号放射科医师,2.473±0.09和10.382 ±0.63。
(3)二维和三维分形分析具有良好的组间重复性;1号放射科医师的二维和三维分形分析的分维数的平均差异分别为-0.024 (95%一致性极限:-0.212,0.372)和-0.024(95%一致性极限:-0.307,0.355),2号放射科医师的二维和三维分形分析的分形丰度的平均差异分别为-0.355 (95%一致性极限:-0.869,1.579)和-0.043 (95%一致性极限:-1.154,1.239)。
对于临床的意义:
分形分析可以重复应用于局部血流量的空间异质性的测量,以提供血流异质性的临床数据。
[1]O’Connor JP,Rose CJ,Jackson A,et al.DCE-MRI biomarkers of tumour heterogeneity predict CRC liver metastasis shrinkage following bevacizumab and FOLFOX-6[J].Br J Cancer,2011,105(1):139-145.
[2]Alic L,van Vliet M,van Dijke CF,et al.Heterogeneity in DCEMRI parametric maps:a biomarker for treatment response?[J].Phys Med Biol,2011,56(6):1601-1616.
[3]Rose CJ,Mills SJ,O’Connor JP,et al.Quantifying spatial heterogeneity in dynamic contrast-enhanced MRI parameter maps[J].Magn Reson Med,2009,62(2):488-499.
[4]Craciunescu OI,Das SK,Clegg ST.Dynamic contrastenhanced MRI and fractal characteristics of percolation clusters in two-dimensional tumor blood perfusion[J].J Biomech Eng,1999,121(5):480-486.
[5]Goh V,Sanghera B,Wellsted DM,et al.Assessment of the spatial pattern of colorectal tumour perfusion estimated at perfusion CT using two-dimensional fractal analysis[J].Eur Radiol,2009,19(6):1358-1365.
[6]Lind JS,Meijerink MR,Dingemans AM,et al.Dynamic contrastenhanced CT in patients treated with sorafenib and erlotinib for non-small cell lung cancer: a new method of monitoring treatment?[J].Eur Radiol,2010,20(12):2890-2898.
[7]Fournier LS,Oudard S,Thiam R,et al.Metastaticrenal carcinoma:evaluation of antiangiogenic therapy with dynamic contrastenhanced CT[J].Radiology,2010,256(2):511-518.
[8]Smith TG Jr,Lange GD,Marks WB.Fractal methods and results in cellular morphology:dimensions, lacunarity and multifractals[J].J Neurosci Methods,1996,69(2):123-136.
[9]Plotnick RE,Gardner RH,Hargrove WW,et al.Lacunarity analysis: a general technique for the analysis of spatial patterns[J].Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics,1996,53(5):5461-5468.
[10]Bland JM,Altman DG.Statistical methods for assessing agreement between two methods of clinical measurement[J].Lancet,1986,1(8476):307-310.
[11]Kiessling F,Boese J,Corvinus C,et al.Perfusion CT in patients with advanced bronchial carcinomas:a novel chance for characterization and treatment monitoring?[J].Eur Radiol,2004,14(7):1226-1233.
[12]Eberhard A,Kahlert S,Goede V,et al.Heterogeneity of angiogenesis and blood vessel maturation in human tumors:implications for antiangiogenic tumor therapies[J].Cancer Res,2000,60(5):1388-1393.
[13]Vaupel P,Mayer A.Hypoxia in cancer:significance and impact on clinical outcome[J].Cancer Metastasis Rev,2007,26(2):225-239.
[14]Gazit Y,Baish JW,Safabakhsh N,et al.Fractal characteristics of tumor vascular architecture during tumor growth and regression[J].Microcirculation,1997,4(4):395-402.
[15]Veenland JF,Grashius JL,van der Meer F,et al.Estimation of fractal dimension in radiographs[J].Med Phys,1996,23(4):585-594.
[16]Kido S,Kuriyama K,Higashiyama M,et al.Fractal analysis of internal and peripheral textures of small peripheral bronchogenic carcinomas in thinsection computed tomography: comparison of bronchioloalveolar cell carcinomas with nonbronchioloalveolar cell carcinomas[J].J Comput Assist Tomogr,2003,27(1):56-61.
[17]Kido S,Kuriyama K,Higashiyama M,et al.Fractal analysis of small peripheral pulmonary nodules in thin-section CT:evaluation of the lung-nodule interfaces[J].J Comput Assist Tomogr,2002,26(4):573-578.
[18]Dougherty G,Henebry GM.Lacunarity analysis of spatial pattern in CT images of vertebral trabecular bone for assessing osteoporosis[J].Med Eng Phys,2002,24(2):129-138.
[19]Lopes R,Betrouni N.Fractal and multifractal analysis:a review[J].Med Image Anal,2009,13(4):634-649.

