基于演化图的导航星座星间路由算法
王彦 刘波 虞万荣 赵宝康
(国防科学技术大学计算机学院,长沙410073)
1 引言
近年来,全球卫星导航系统在国民经济和国防军事等领域的应用日益广泛和深入,推动着其技术的不断进步和功能的持续完善。美国的GPS率先实现了星间链路,并且计划在GPS III中装配指向性天线,并引入路由转发机制,以提升星间链路数据通信性能[1]。总结国外卫星导航系统的发展经验,在星座内建立星间链路,并利用星间链路进行星间测距和数据通信,以实现星座的自主运行是一种发展趋势[2]。本文针对导航星座星间数据通信的需求,对导航星座星间路由相关问题展开研究。
针对基于星间链路的卫星星座系统星间路由问题,国内外众多学者已进行了大量的研究工作,但大多数工作都是针对用于承载地面用户数据流量的卫星通信系统的星间路由问题,鲜有学者针对导航星座进行星间路由研究。文献[3]提出了一种基于地面站集中式的导航星座星间路由算法,其假设条件是:星座系统的星间链路资源丰富,一颗卫星可在同一时刻与其他多颗卫星建立星间链路,确保星座网络拓扑在任意时刻处于全连通状态。但在星间链路资源受限的情况下,一颗导航卫星无法同时建立并维持多条星间链路,将持续进行星间链路切换并导致星座网络拓扑处于非连通状态,上述方法将难以有效地解决星间路由问题。
为降低导航星座星间数据通信对地面站的依赖,星上在线计算的路由算法是未来发展的必然趋势。本文针对装配指向性天线、具有确定性链路调度的卫星导航星座系统,充分分析了由卫星在轨飞行及星间链路调度切换所导致的星座动态变化的网络拓扑结构,引入演化图模型[4],对星座动态变化的网络拓扑结构进行建模,提出一种星间最早到达路径的路由算法,再给定导航星座构型及星间链路调度方案,对算法进行模拟验证。
2 导航星座动态网络拓扑结构的演化图建模
2.1 场景描述
图1给出了6个连续时间间隔的导航星座网络拓扑结构快照,每个时间间隔长度固定为Δt。为简化描述,图1中只给出了导航星座中的一部分导航卫星及这些导航卫星之间建有的星间链路。如图1所示,将导航卫星分别记为A、B、C、D、E、F和G;以A与C之间的星间链路为例,将导航卫星间的星间链路记为ISL(A,C)。在每个时间间隔内,导航星座中的每颗卫星或选择与另一颗特定的卫星建立一条全双工的星间链路,或处于空闲状态;但不能同时与多颗卫星建立星间链路,故在每个时间间隔内导航星座网络拓扑都处于非连通状态[5]。由于导航星座具有确定性的星间链路调度,星座中的每颗导航星都可获得当前时间间隔内和后续一定时间间隔内整个导航星座网络拓扑信息。
观察图1,在从0~6Δt的每个时间间隔内,导航星座的网络拓扑结构都是固定不变的,但都处于非连通状态;且在任意一个时间间隔内,A与G之间都未建立星间链路。由于在同一时刻,每颗卫星至多只能建立一条星间链路,故不可能在导航星座网络拓扑结构不发生变化的一个时间间隔内找到一条从A至G的路径。然而,可通过导航星座网络拓扑结构随着每个时间间隔的变化,在时域空间中找到从A至G的路径。例如,在0~Δt内,从A出发到达C,在2Δt~3Δt内,再从C出发就可到达G。
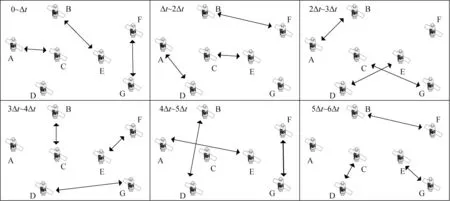
图1 不同时间间隔内导航星座网络拓扑结构快照Fig.1 Snapshots taken at different time intervals of the network topology of navigation constellation
2.2 导航星座动态网络拓扑结构的演化图模型
给定图G=(V,E),及图G的有序静态子图SG=G1,G2,…,GL使得可定义EG= (G,SG)为演化图[6]。令EEG=∪Ei,定义M为演化图EG中边的数目,M=|EEG|,令VEG=∪Vi,定义N为演化图EG中节点的数目,N=|VEG|。对应至导航星座,Gi是对导航星座处在第i个时间间隔时的网络拓扑结构的描述,M为星座在一段时间内所建立的星间链路的条数,N为星座在一段时间内处于运行状态的导航卫星的颗数。图2给出了图1所对应的从0~6Δt,共6个时间间隔内的导航星座的动态网络拓扑的演化图模型。图2中星间链路上标记的数字表示卫星间建立该星间链路时所处的时间间隔。
给定演化图EG中的节点v∈VEG及边e∈VEG。定义节点v的动态度为在演化图EG其他节点中与节点v间存在边调度的节点的个数,记为δv;定义边e的动态度为演化图EG对该边的调度次数,记为δe;定义演化图EG的最大节点动态度δV=max{δv,v∈VEG},最大边动态度δE=max{δe,e∈EEG}。如图2有,δA=4,表示A在0~6Δt内分别与其他4颗导航卫星建立了星间链路;δISL(B,F)=2, 表示B与F之间在0~6Δt内建立了两次星间链路;δV=6,即表示在0~6Δt内,E分别与其他6颗导航卫星建立了星间链路;δE=δISL(B,F)=δISL(F,G)=2,即表示在0~6Δt内,B与F之间及F与G之间分别建立了两次星间链路。
给定演化图EG,可定义如下函数:
1)函数ζ(e,r)→tld,有e∈EEG,r∈N+及tld∈T,给出在演化图EG中第r次调度e时所处时间间隔内,e的传播时延tld。如图2,在第2个时间间隔,B与F间第1次建立星间链路,假定此时B与F之间的星间距离为27 900km,则B与F间的星间链路时延为93ms,故有ζ[ISL(B,F),1]=93ms;在第6个时间间隔,B与F间第2次建立星间链路,假定此时B与F之间的星间距离为28 500km,则B与F间的星间链路时延为95ms,故有ζ[ISL(B,F),2]=95ms。在本文讨论中,假设在同一个时间间隔内,星间链路时延保持不变。
2)函数S(e,r)→ [tsi,tei],有e∈EEG,r∈N+及tsi,tei∈T,且tsi<tei, 给出在演化图EG中第r次调度e的时间间隔[tsi,tei],其中tsi是时间间隔的起始时刻,而tei是时间间隔的终止时刻。如图2,在第3个时间间隔,A与B间第1次建立星间链路,故有S[ISL(A,B),1]=[2Δt,3Δt]。
3)函数f(e,t)→[tet,tld],有e∈EEG及t,tet,tld∈T, 给出在演化图EG中t时刻后e可进行传输的最早时刻tet,及此时e的传播时延tld。若在t时刻后,演化图EG中不存在对e的调度,则有tet=tld=∞。如图2,在时刻2.5Δt后,C与G在第3个时间间隔[2Δt,3Δt]内建立了星间链路,则在时刻2.5Δt,C可向G进行数据传输,假定此时C与G间的星间距离为27 000km,则C与G间的星间链路时延为90ms,故有f[ISL(C,G),2.5Δt]=(2.5Δt,90ms); 而在时刻3Δt后,C与G之间没有星间链路的建立,故有f[ISL(C,G),3Δt]=(∞,∞)。
给定图G中的路径R=e1,e2,…,ek,有e∈EEG,及Rσ=σ1,σ2,…,σk,有σi∈T,σi表示ei的起始传输时刻。定义J=(R,Rσ)为演化图EG中的一条路径 (当且仅当Rσ与R、ζ、S保持一致)。Rσ与R、ζ、S保持一致是指,对于任意的ei、σi,存在ri∈N+,且1≤ri≤δE(ei),使得σi∈S(ei,ri)并且σi+ζ(ei,ri)∈S(ei,ri)。 给定演化图EG中的任意两个节点u和v,时刻t,起始时刻为t的从u到v的路径可表示为J(u→v,t)。
给定演化图EG中的路径J= (R,Rσ),R=e1,e2,…,ek,Rσ=σ1,σ2,…,σk,有如下定义:
1)路径J的跳数为h(J),则有h(J)=|R|=k,即构成路径的边的数目。
2)路径J的起始时刻为s(J),即路径源节点发起路径请求的时刻。
3)路径J的到达时刻为a(J),则有a(J)=σk+tld[f(ek,σk)],即路径所调度的最后一条边ek的起始传输时刻与此时边ek的传播时延之和。
4)路径J的时间开销为c(J),则有c(J)=a(J)-s(J),即路径到达时刻与路径起始时刻之差。
给定演化图EG中的任意两个节点s和v,时刻t。起始时刻为t的从s到v的最早到达路径定义为JE(s→v,t)∈ {J(s→v,t)|min[c(J)]}; 记JE(s→v,t)的到达节点v的时刻为a[(s,v),t],则有a[(s,v),t]=c[JE(s→v,t)]+t。若在路径JE(s→v,t)上,节点u是节点v的直接前驱节点, 则有a[(s,v),t]=tet{f[(u,v),a[(s,u),t]]}+tld{f[(u,v),a[(s,u),t]]}。
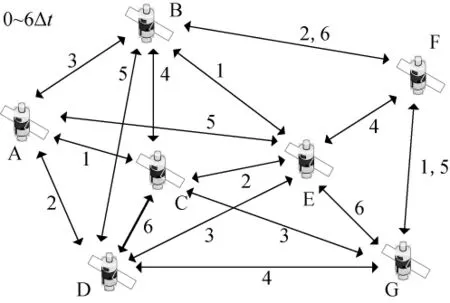
图2 动态网络拓扑的演化图模型Fig.2 Evolving graph model ofdynamic network topology
2.3 数据结构表示
描述导航星座动态网络拓扑结构的演化图模型的数据结构如图3所示。由于本文考虑的导航星座内建立的星间链路较少,因此采用邻接链表表示导航星座动态网络拓扑结构的演化图模型可以取得较优的存储开销,该邻接链表的存储开销为O(MδE+NδV)[4]。
演化图的邻接链表表示法就是对演化图中的每个节点,用一个单向链表列出从该节点发出的所有边,链表中每个单元对应于一条边,为记录每条边的相关信息,链表中的每个单元除列下一条边的另一个端点外,还需包含相应的数据域以储存这条边的相关信息。例如,图3中卫星节点u在一段时间内与δu颗卫星节点建立了星间链路,卫星节点u所对应的邻接链表的长度即为δu;卫星节点u与相邻卫星节点v1建立了δISL(u,v1)次星间链路,S[ISL(u,v1),1]和ζ[ISL(u,v1),1]记录了卫星节点u与相邻卫星节点v1第一次建立的星间链路的相关信息,其中S[ISL(u,v1),1]为星间链路的调度时间间隔,ζ[ISL(u,v1),1]为星间链路的链路时延。注意,图3中相邻卫星节点的概念是指两颗卫星之间有建立星间链路,而不是指一颗卫星与另一颗卫星在轨道物理位置上的相邻。

图3 演化图模型的数据结构Fig.3 Data structure for evolving graph
3 基于演化图模型的星间路径计算
由于导航星座在轨运动具有周期性和可预测性,再结合星间链路调度的确定性,星座中的每颗导航星都可获得足够导航星座网络拓扑信息以在星上独立地进行在线路由计算。算法的基本思想在于:适应导航星座网络拓扑的急剧变化,并正确给出任意起始时刻的任意两颗卫星之间的最早到达路径。
3.1 最早到达路径算法
Dijkstra最短路径算法[6]中的最短路径能保持所谓的前向路径属性,即最短路径的任意前向路径都是最短路径。文献[7]证明了在演化图模型中有且仅有一条最早到达路径能保持前向路径属性。在演化图模型中计算路径起始时刻为t的单源节点s到所有节点最早到达路径算法的输入、输出及步骤具体如下:
变量:演化图EG,节点s∈VEG,时刻t∈T。
输出:数组tEAD[v]∈T,给出在时刻t后从节点s至每个节点v∈VEG的最早到达路径的到达时刻;数组father[v]∈VEG,给出每个节点v≠s∈VEG在最早到达路径上的直接前驱节点。
变量:最小优先队列Q,按键值tEAD排序;集合C,记录已完成最早达到路径计算的节点。
步骤1 初始化tEAD[s]=t,对所有v∉VEG,令tEAD[s]=∞;以s为首节点创建最小优先队列Q;初始化集合C为空。
步骤2 若Q为空,转至步骤5;否则,提取Q的首节点u出列。
步骤3 遍历节点u的邻接表,对每个不在C中的邻居节点v,令 (tet,tld)=f[(u,v),tEAD[u]]。 若tet+tld≥tEAD[v], 继续步骤3;否则,令tEAD[v]=tet+tld,father[v]=u, 查找节点v是否已插入至Q中。若在Q中,则节点v的键值已被更改,更新Q;否则,将节点v插入Q。继续步骤3。
步骤4 将节点u插入C,转至步骤2。
步骤5 算法结束,输出结果。
3.2 算法证明与复杂度分析
要证明对演化图EG运行最早到达路径算法可给出t时刻后从节点s到所有节点u∈VEG的最早到达路径,只需证明在算法终止时,对所有节点u∈VEG,有tEAD[u]=a((s,u),t)即可。由于算法运行过程中,演化图EG中的任意节点u只被插入C一次。上述证明可转化为,将节点u插入C后有tEAD[u]=a((s,u),t)。 算法初始时,有C={s},及tEAD[s]=t=a((s,s),t)。当算法运行至将某一节点v插入C的前一时刻,这时节点v被插入Q后已经从Q中出列,显然此时已有路径将节点s与节点v连接;假设路径J是当前从节点s到节点v的最早到达路径,则路径J可将C中的节点s连接至C外的节点v;若此时节点w是路径J上第一个不在C内的节点,并且在路径J上节点u是节点w的直接前驱,则节点u已经被插入至C中,执行步骤3后应有tEAD[u]=a((s,u),t);当节点u被插入C时,节点w已经被插入至Q中,并且节点w不可能是路径J上节点v的后继节点,此时算法已运行至将节点v插入C的前一时刻,故有v=w;根据最早到达路径 的 属 性, 有a[(s,v),t]=tet{f[(u,v),a[(s,u),t]]}+tld{f[(u,v),a[(s,u),t]]};算法下一步执行将节点v插入C的操作,执行后有tEAD[v]=a[(s,v),t]。 算法终止时,显然有C=VEG。
最早到达路径算法的运行时间主要取决于函数f(·)及最小优先队列Q的具体实现。根据图3给出的数据结构,采用二分搜索,可在O(lnδE)的时间内完成函数f(·)的计算。若采用二叉最小堆来实现最小优先队列,则Q的插入、查找、提取和更新操作都需要O(lnN)的时间[6]。在算法运行过程中,对每个插入C中的节点u,步骤3对节点u的不在C中每个邻居节点执行函数f(·)的计算及队列Q的相关操作,耗时为O(lnδE+lnN)。函数f(·)的计算及队列Q的相关操作最多执行M次,故算法总计运行时间为O[M(lnδE+lnN)]。
4 算法模拟与结果分析
4.1 相关模拟参数设置
导航星座选择Walker-δ24/3/2星座构型,轨道高度为21 000km,轨道倾角为55°,星座回归周期大约为15h,星座中所建立的星间链路的指向方位角限定在[-60°,60°]。
可将星座中的3个轨道面命名为轨道面1、2、3,用1L、2M、3N表示轨道面1、2、3中的第L、M、N颗卫星。星座中的每颗卫星可见的卫星有22颗,每个轨道面内相位差为180°的两颗卫星由于地球的阻挡而相互不可见。例如,卫星11和卫星15,由于在同一轨道面内,并且相位角相差180°,为两颗相互不可见的卫星。
由于受到星间链路指向方位角的限制,并不是所有可见卫星之间都可建立星间链路。在星间链路指向方位角限定在 [-60°,60°]内的条件下,星座中的每颗卫星可与14~16颗卫星建立星间链路。导航星座内建立星间链路采用矩阵变换规划方法[8],并选定时间间隔为3s。
4.2 路径的时间开销与跳数
在星座回归周期大约为15h的条件下,算法模拟从0h开始并每隔0.5h选择一个路径起始时刻,共选择30个路径起始时刻点,计算了星座内所有卫星间、同轨卫星间及异轨卫星间的最早到达路径。图4和图5分别给出了最早到达路径的时间开销与转发跳数的平均值。同轨卫星间最早到达路径的时间开销要小于异轨卫星间的;同时,同轨卫星间最早到达路径的转发跳数也要小于异轨卫星间的。所有卫星间最早到达路径的平均时间开销约为14s,平均转发跳数约为2.5。

图4 最早到达路径的时间开销Fig.4 Time cost of earliest journey

图5 最早到达路径的跳数Fig.5 Hops of earliest journey
4.3 路径随起始时刻的变化
为反应星间路径随路径起始时刻的变化情况,算法模拟给出了在不同路径起始时刻卫星11与卫星15之间的最早到达路径。分析表1可知,在0.0~21.0s间的8个不同路径起始时刻下,卫星11与卫星15之间的最早到达路径在第6.0s、9.0s、12.0s和18.0s发生了切换。

表1 最早到达时刻路径随起始时刻的变化Tab.1 Changing of the earliest journey along with the starting time
5 结束语
本文主要研究了导航星座星间路由的相关问题。在导航星座星间链路资源受限,不能确保星座网络拓扑处于全连通状态的条件下,传统的方法无法解决星座中任意两颗卫星间的路由问题。导航星座星间链路调度的确定性使得导航卫星可准确地预测后续一段时间内星座网络拓扑的动态变化情况;利用演化图对导航星座网络拓扑结构进行建模,基于演化图的路由算法有效地解决了星座网络拓扑非连通状态条件下星座中任意两颗卫星间的最早到达路由问题。
进一步工作可考虑结合导航卫星数据传输的流量模型,对星间链路建立方案和星间路由策略进行联合优化,以提高星间链路资源的利用率,满足导航卫星间各类型数据传输的需求。
[1]MAINE K P,ANDERSON P,BAYUK F.Communication architecture for GPS III[C].IEEE Aerospace Conference,Big Sky,MT,March 6-13,2004.
[2]陈贵忠,帅平,曲广吉.现代卫星导航系统技术特点与发展趋势分析 [J].中国科学·技术科学,2009,39(4):686-695.CHEN GUIZHONG,SHUAI PING,QU GUANGJI.Technical characteristics and development trend analysis of modern navigation satellite systems[J].Scientia Sinica,Technologica,2009,39(4):686-695.
[3]李振东,何善宝,刘崇华.一种适用于导航卫星星间链路的动态路由算法 [C].第2届中国卫星导航学术年会,上海,2011.LI ZHENDONG,HE SHANBAO,LIU CHONGHUA.An active routing algorithm for navigation satellite constellation inter-satellite links[C].The 2ndChina Satellite Navigation Conference,Shanghai,2011.
[4]FERREIRA A.Building a reference combinatorial model for MANETs [J].IEEE Network,2004,18(5):24-29.
[5]范丽,张育林.Walker星座星间链路构建准则及优化设计研究 [J].飞行力学,2007,25(2):93-96.FAN LI,ZHANG YULIN.Construction rules and design optimization of ISLs in Walker constellation[J].Flight Dynamics,2007,25(2):93-96.
[6]CORMEN T H,LEISERSON C E,RIVEST R L.Introduction to algorithms[M].2nd ed.Cambridge:The MIT Press,2004.
[7]BUIXUAN B,FERREIRA A,JARRY A.Evolving graph and least cost journeys in dynamic networks[C].Modeling and Optimization in Mobile,Ad Hoc and Wireless Networks,WiOpt′03,Sophia-Atipolis,2003.
[8]林金茂,杨俊,王跃科.基于矩阵变换的GNSS星间链路最优规划算法 [C].第2届中国卫星导航学术年会,上海,2011.LIN JINMAO,YANG JUN,WANG YUEKE.Optimizing algorithm for the scheduling of GNSS crosslink:a matrix transform approach [C].The 2ndChina Satellite Navigation Conference,Shanghai,2011.

