航天器规避动态障碍物的自适应人工势函数制导

高鹏 罗建军

（1西北工业大学航天学院，西安710072）（2航天飞行动力学技术重点实验室，西安710072）

1 引言

人工势函数 （Artificial Potential Function，APF）制导方法具有在复杂环境下形式简单、计算量小等优点，近年来在空间近距离接近和操作方面得到了广泛关注。文献［1］将APF方法应用到航天器自主避障的轨道设计中，将追踪航天器在障碍物约束条件下的运动转化为在势力场中的运动，并以逻辑判断的形式进行末制导。文献［2-3］研究了在国际空间站的交会对接和近距离作业中，采用势函数制导的安全自主近距离机动，对有静态路径约束的势函数制导算法进行了开发和评估。文献［4］针对非合作目标，研究了规避静态障碍物的势函数制导，并且在末制导阶段考虑安全走廊。文献［5］将人工势函数法与模糊控制方法结合起来，考虑规避动态障碍物，安全、快速地逼近目标。文献［6］提出一种自适应的人工势函数制导方法，针对静态障碍物，研究了航天器近距离操作中的轨道和姿态运动快速规划，比传统人工势函数制导方法更加节省燃料。上述研究大多针对静态障碍物，且引入的斥力函数会使总的势函数在收敛点处的值不为零，并且没有考虑速度变化对引力势函数的影响，影响了收敛精度和燃料消耗。

为此，本文首先针对传统人工势函数制导中引入斥力函数会使势函数在收敛点处的值不为零的情况，对斥力函数乘以修正项，使得在收敛点势函数为零。然后，在规避静态障碍物的基础上，研究了规避动态障碍物的势函数制导。最后，针对传统人工势函数没有考虑速度变化的不足，考虑速度与引力梯度场之间的关系，采用负反馈，使引力梯度场 “适应”速度变化，研究规避动态障碍物的自适应人工势函数 （AAPF）制导，并比较APF制导与AAPF制导的收敛精度和燃料消耗。本文研究的AAPF制导可用于航天器近距离安全接近的高精度、燃料较省的制导和控制任务中。

2 相对运动模型

若两航天器运行在近圆轨道上，相邻航天器在目标航天器轨道系中的相对运动可用C-W方程描述。定义目标航天器轨道坐标系为O-xyz：原点O在目标航天器质心，Ox轴由地心指向目标航天器，Oy轴在轨道平面内与Ox轴垂直并指向目标航天器前进方向，Oz轴按右手法则确定。在目标航天器轨道坐标系O-xyz中，将C-W方程写为状态空间方程形式：

当f＝0，给定初始条件r0，v0，rf，再给定转移时间T，对式（1）进行求解，可以得到

式中Φ11（T），Φ12（T），Φ21（T），Φ22（T）均为状态转移矩阵。

所需施加速度脉冲：

进而可以得出脉冲作用后的任意时刻t的速度的表达式：

式中 上标 “＋”号表示脉冲作用后的状态。

3 规避动态障碍物的自适应人工势函数制导

所谓 “障碍物”是指在航天器的飞行轨道上或追踪航天器接近目标航天器的规划路径上，阻碍航天器飞行或对其飞行安全造成威胁的空间物体，也可以是一些飞行路径约束。通常是在规划路径上飞行的航天器、空间碎片或假设的航路点约束、飞行路径和区域限制等。动态障碍物是指其相对于目标航天器的相对运动速度不为零。

3.1 人工势函数制导

规避动态障碍物的人工势函数制导方法的主要思想是：以追踪航天器安全有效地接近目标航天器为目标，首先定义一个合适的标量势函数，该势函数在期望的目标状态位置具有全局最小值，并且用具有较高势函数值的区域表示运动路径的限制条件或对障碍物的规避，其中高值势函数区域的梯度值直接反映了施加在被控对象上规避障碍物或禁飞区域的斥力大小；然后选择适当的控制律使势函数的导数为负定，这样便可以应用Lyapunov稳定性理论确保航天器的速度和位置均收敛于期望的目标状态点，且不违背路径限制条件，从而在追踪航天器接近目标航天器的过程中，实现对追踪航天器在整个状态空间中的运动趋势控制和对障碍物的规避［4］。

在存在障碍物情况下，势函数φ为引力势能函数φa与斥力势能函数φr之和，即有φ＝φa＋φr。通常选取φr为高斯函数形式，即

式中ψ和σ为斥力势的高和宽；ri表示第i个障碍物在目标航天器轨道系下的相对位置矢量；矩阵Ni是与障碍物形状有关的外形矩阵，当Ni＝I时，障碍物是以ri为中心的球形。考虑到采用式（3）作为φr会导致φ在r＝rf处的值不为零，即势能函数在期望的平衡点处的值不为零，导致平衡点偏离，精度降低。若选择Lyapunov函数为势函数，则不满足Lyapunov稳定性条件。为使势能在引入斥力势能之后，在收敛点处的值为零，可将障碍物斥力势的表达式修正为［4］

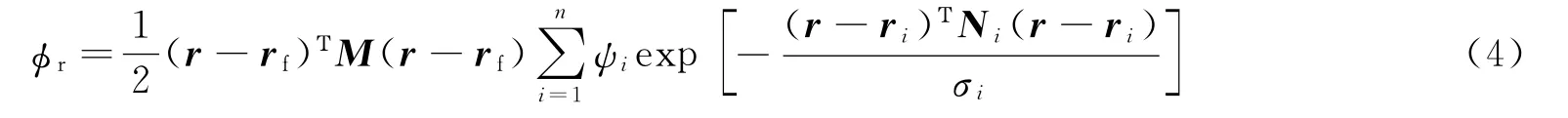
这样，修正后的势函数为

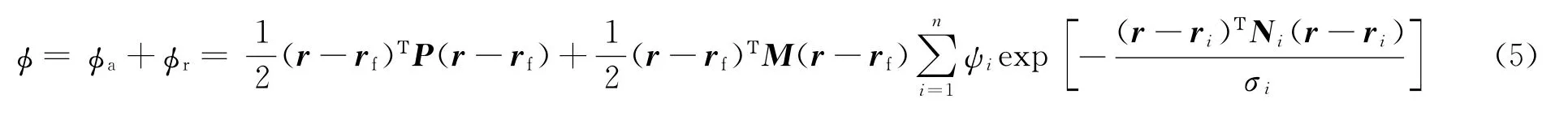
式中P为正定对称矩阵；M为正定对称矩阵。

为使追踪航天器一直沿着势能降低的方向运动，需要对航天器施加控制脉冲作用。施加控制作用的判断条件是：势能是否降低。如果势能降低，则沿着运动方向继续运动；如果势能增加或不变，则施加沿势能梯度方向相反的控制脉冲，使航天器沿着势能降低的方向运动。控制作用的数学表达式为［1］

式中u表示控制脉冲；k为大于零的常数；符号 “∇”表示梯度运算；上标 “-”表示速度脉冲作用前的状态。整个近距离操作过程中的总控制脉冲消耗为所有时刻所施加的控制脉冲的‖·‖1求和，即

对于动态障碍物，势函数在障碍物相对位置矢量下的梯度为

势函数对时间的导数为

3.2 自适应人工势函数制导及稳定性分析

对于航天器近距离空间操作任务，要求追踪航天器能够平稳接近目标航天器，需要均匀施加控制作用，而传统人工势函数没有考虑速度变化对控制作用的影响。这样，由于初始时刻相对速度与引力势能梯度相差较大，需施加很大的控制作用；末时刻相对速度与引力势能梯度相差较小，施加的控制作用很小。整个过程控制作用大小和时间不够合理，会导致末端收敛较慢，精度不高，甚至在收敛点附近震荡。针对上述不足，文献 ［6］考虑速度变化对控制作用的影响，研究了规避静态障碍物的自适应人工势函数制导。本文将该方法推广应用于规避动态障碍物的制导。

自适应人工势函数制导认为引力势能的权重为时变的，并使追踪航天器在施加控制作用之后的引力势能的梯度 “适应”速度的变化，从而实现航天器近距离接近的快速、较省燃料的自适应制导，其控制律为［6］

式中φ和可通过式（5）和式（9）得到；R为引力梯度系数三角分解后的上三角矩阵，其计算过程如下［6］。

为使追踪航天器在施加控制作用之后的引力势能的梯度 “适应”速度的变化，定义广义误差向量为施加速度脉冲后的速度与引力势能梯度之差，即e＝＋-（-∇rφa）。考虑到引力势能的权重为时变的，即P＝P（t），采用三角分解P（t）＝RΤ（t）R（t），有

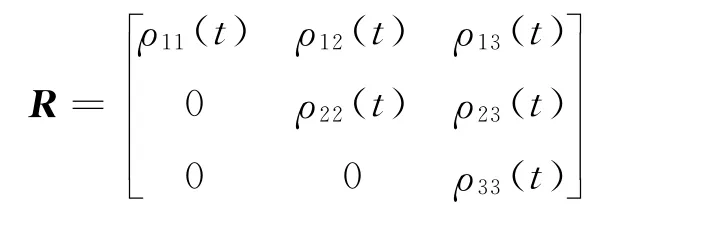
则引力势的导数变为

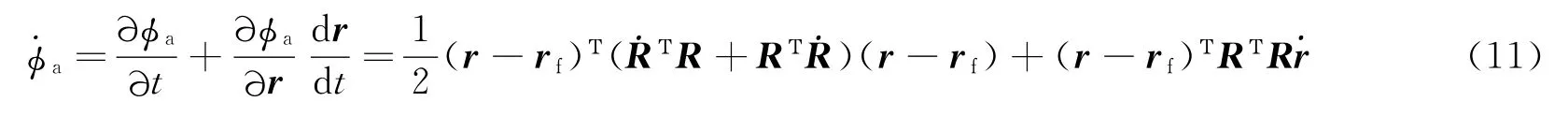
根据式（2）可计算出在任意位置r，t＝0时刻的速度为

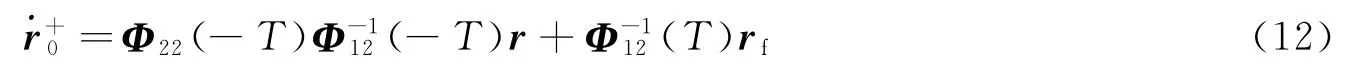
这样，广义误差为

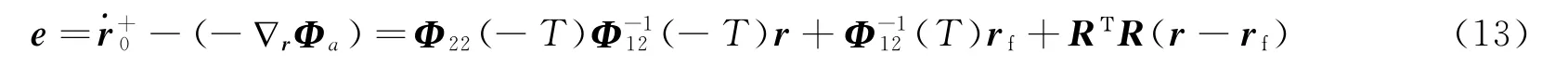
对式（13）求导可得

通过适当的变形，有

其中

为使e→0，设计负反馈，令＝-e，得到

为判断所采用的自适应人工势函数制导方法在收敛点处的稳定性，下面采用选取Lyapunov函数V＝φ，引力势能的时变权重P（t）＝RΤR，利用Lyapunov第二法对自适应人工势函数制导的稳定性进行分析。

1）对于任意的r≠0，都有V＞0，当r＝0时，V＝0；

2）当 ‖r‖ →＋∞时，V→＋∞；

3）当˙V＞0时，利用式（4）、式（10）和式（11），可得

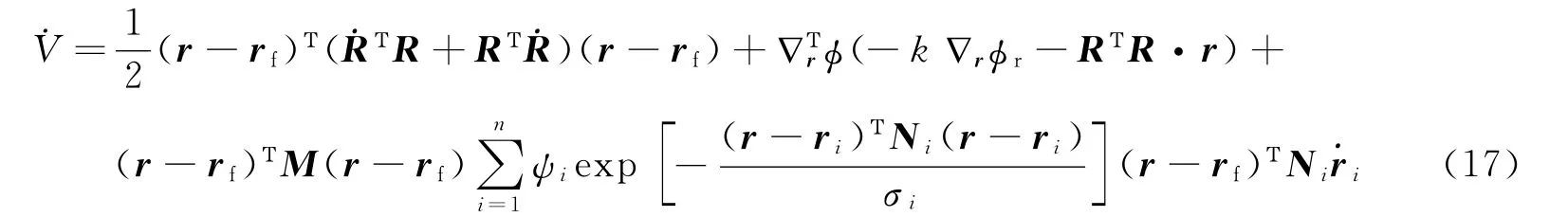
其中r及为有界向量，RΤR为系数矩阵，当转移时间给定，其他参数均为常值，那么必定存同理，对于第三项，必定存在一个δ2＞0，使得对于第二项·r，该项中只有第一、三项与k有关，其他两项均为有限值。故通过以上分析，可以得到则存在一个k＞0值，可以使得

4 仿真计算与结果分析

以与运行在轨道高度为700km圆轨道的目标航天器交会对接为例，对APF和AAPF规避障碍物的性能进行仿真。取初始相对位置r0＝［400 500 600］Tm，初始相对速度v0＝［000］Tm／s，末点相对位置rf＝［000］Tm，末点相对速度vf＝［000］Tm／s。

为验证AAPF制导是否具有规避动态障碍物的能力，任意选取一个动态障碍物，相关的参数及障碍物选取：变量障碍物初始位置障碍物的移动速度其他相关参数设置如下：

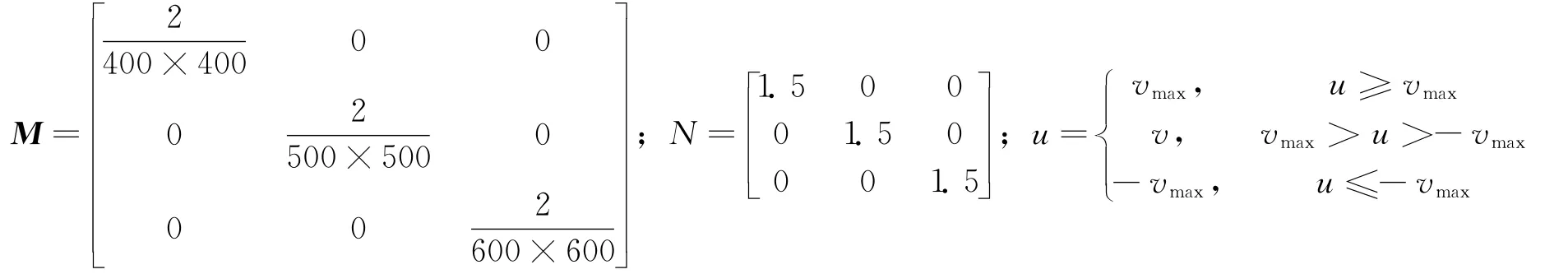
式中vmax＝1m／s；ψ＝1.5×105；σ＝900；k＝0.002；仿真步长1s；总仿真时间3 000s；采用四阶龙格库塔进行数值积分。追踪航天器的相对运动状态变量及控制作用随时间的变化曲线如图1和图2所示。

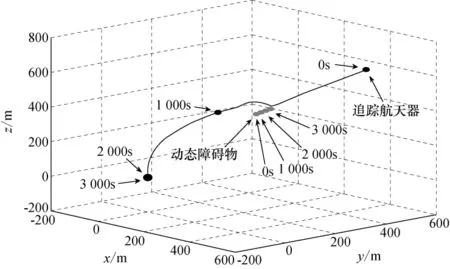
图1 追踪航天器和障碍物相对目标航天器的运动轨迹Fig.1 Relative moving trajectories of the chaser and obstacle with respect to the target

图2 追踪航天器相对位置、相对速度和施加的控制脉冲随时间的变化Fig.2 Relative position，relative velocity and the control histories of the chaser

由图1和图2可以看出：追踪航天器在AAPF制导律控制作用下，在1 000s之前，成功避开了障碍物，在2 000s之前相对位置、速度矢量均已收敛至0；在整个仿真中AAPF制导控制作用的大小和时间比较合理，这是由于在自适应控制律中考虑了 “适应”速度变化的结果。说明了AAPF制导律的正确性与有效性。

为比较APF和AAPF这两种制导律的效能，分别考虑无障碍物、静态障碍物、动态障碍物这3种情况，数值仿真结果如表1所示。另外，为验证对斥力势乘以修正项是否能够提高收敛精度，在相同的初始条件下，对未引入修正项的制导方式进行计算，计算结果如表2所示。

由表1中两种制导律的对比可以看出，在同样的初始条件下，在逼近精度方面，AAPF制导比APF制导至少高两个量级；在速度脉冲消耗方面，前者比后者大约节省30%。这表明，AAPF制导在考虑了速度变化影响后，比APF制导更加节省燃料和具有更高的精度。由表1和表2中相同制导方式的对比可以看出，对斥力势乘以修正项比未乘以修正项的收敛精度更高。

表1 不同制导方式的计算结果 （有修正项）Tab.1 Results of different guidance methods （with correction term）

表2 不同制导方式的计算结果 （无修正项）Tab.2 Results of different guidance methods （without correction term）

5 结束语

根据航天器近距离操作中，追踪航天器在向目标航天器逼近过程中规避动态障碍物的需求，本文在能够规避静态障碍物的传统人工势函数制导方法的基础上，研究了规避动态障碍物的人工势函数制导方法。考虑到在有障碍物情况下，引入斥力势会使总的势能函数在收敛点处的值不为0，使得收敛点偏离，影响收敛精度；在斥力势中加入修正项，使势能函数在收敛点处为零，从而提高收敛精度。在此基础上，研究了规避动态障碍物的自适应人工势函数制导。通过理论分析与仿真验证，得到的主要结论有：

1）通过引入修正项，使得势函数在收敛点处的值为零，能够提高追踪航天器逼近的收敛精度。

2）APF与AAPF两种制导律均能使追踪航天器成功避开动态障碍物，向目标点逼近；AAPF制导方法与APF相比，由于考虑了对速度变化的 “适应”，控制脉冲作用施加更加合理，减少了总速度脉冲消耗，且具有更高的精度。

［1］ISMAEL LOPEZ，COLIN R MCINNES.Autonomous rendezvous using artificial potential function guidance ［J］.Journal of Guidance Control and Dynamics，1995，18（2）：237-241.

［2］COLIN R MCINNES.Autonomous path planning for on-orbit servicing vehicles ［J］.Journal of the British in terplanetary Society，2000，53（1／2）：26-38.

［3］ENDER ST JOHN OLCAYTO，COLIN R MCINNES，FINN ANKERSEN.Safety-critical autonomous spacecraft proximity operations via potential function guidance［C］.45th AIAA Aerospace Sciences Meeting and Exhibit，Reno，Nevada，January 8-11，2007.

［4］张大伟，宋申民，裴润，等.非合作目标自主交会对接的椭圆蔓叶线势函数制导 ［J］.宇航学报，2010，10（31）：34-43.ZHANG DAWEI，SONG SHENMIN，PEI RUN，et al.Ellipse cissoid-based potential function guidance for autonomous rendezvous and docking with non-cooperative target［J］.Journal of Astronautics，2010，10（31）：34-43.

［5］ZHANG DAWEI，SONG SHENMIN，PEI RUN.Safe guidance for autonomous rendezvous and docking with a non-cooperative target［C］.AIAA Guidance，Navigation，and Control Conference，Toronto，Ontario，Canada，2010.

［6］JOSUE D MUNOZ，NORMAN G FITZCOY.Rapid path-planning options for autonomous proximity operations of spacecraft［C］.AIAA／AAS Astrodynamics Specialist Conference，August 2-5，2010.