数据网渗透攻击中的拓展的迷宫路径算法

赖 群

(广东电网公司云浮供电局，广东 云浮52730)

网络渗透攻击简称为渗透攻击(Network Penetration)，是攻击者常用的一种攻击手段，也是一种综合的高级攻击技术，指通过一步步渗透，进入某个大型网络主机服务器群组所在的整个网络系统，从而实施网络攻击的技术。由于渗透攻击具有极大的隐蔽性（其在遍历整个网络拓扑结构之前并不发生危害作用），但是一旦其掌握整个网络拓扑结构后，发动的网络攻击往往是致命性的，在该网络系统的任何主机都无法幸免[1]。渗透攻击目前常用的方法是基于攻击图的渗透测试模型攻击图方法 PTGM（Penetration Testing Graph Modal）。

渗透攻击图的自动生成方法有很多，参考文献[2]通过定义攻击模式和prolog规则来自动生成子攻击和攻击图；参考文献[3]建立了网络攻击过程中的贪心策略，并给出该策略的约束攻击图生成过程；而参考文献[4]则利用被测试目标网络脆弱点间的逻辑关系，结合原子攻击知识库，给出一种渗透攻击图自动生成方法。此外，基于生成的渗透攻击图，一些学者还研究了渗透攻击图的优化问题，如参考文献[5]将蚁群算法应用于攻击模型的安全分析中，获取最小关键攻击集的优化解；参考文献[6，7]通过将攻击图与通用安全脆弱点评估系统相结合，删除攻击图中的不可达路径，简化了攻击图。

传统的网络渗透攻击研究对异构网络环境下的攻击研究不足，同时研究重心过多地侧重于被动防护研究，而对主动防御研究不足，导致网络安全研究一直处于被动挨打、疲于应对的局面。通过在网络渗透攻击研究中引入拓展的迷宫路径算法，为异构网络环境下的网络安全研究提供了主动应对策略与方法。通过引入拓展的迷宫路径算法，对任意复杂网络中的关键路径、关键节点进行网络安全策略分析与防护，解决整个网络安全问题提供了切实可行的解决方案。

为了提高对网络渗透攻击的研究，以便对网络渗透攻击进行预防和处理，以计算机算法设计与分析中的迷宫路径算法为蓝本，通过对其进行扩展，尝试对网络拓扑结构进行遍历，在此基础上利用网络攻击方法，实现网络渗透攻击。

迷宫路径算法(Algorithm of Maze’s Path)是一种在已知迷宫存在一条从入口到出口的通路的前提下，寻找到该条迷宫具体路径的算法。迷宫路径算法对于未知图的遍历具有极大的优越性，它可以通过简单有效的算法，在较短时间内寻找到可行路径。该算法在具体实现时，用二维向量对迷宫进行表示。迷宫的入口处一般用向量（0，0）表示，迷宫的出口用二维向量（m，n）表示。 探索者从（0，0）出发，每次只能向前（有 4个可选方向，分别是：正北、正南、正东、正西）行进一步，前进完成后，探索者所在位置由行进前的(i，j)变更为行进后的(i，j+1)、(i，j-1)、(i+1，j)、(i-1，j)（上 述 4 个 位 置依 次对 应向 正北、向正南、向正东、向正西前进）。在行进前同时记录（将信息记录到历史行进记录中）行进前所在位置和行进的具体方向，当行动后的位置可达后，记录行动后的位置。依此顺序前进，当随机选取的行进方向无法抵达时，查找历史行进记录，回退到上一步所在的位置，并按照行进历史记录记载，去探索当前位置未探索的方向。按照这种思路，对整个位置迷宫进行遍历，直到找到出口位置。由于事先已经确定该迷宫存在至少一条明确的由入口到出口的通路，所以迷宫路径算法必然能够寻找到上述路径中的一条。

1 基于拓展迷宫路径算法的网络渗透实现

在进行网络渗透时，网络渗透的最初切入点就可以看做迷宫路径算法中的迷宫入口（Entrance），而迷宫出口（Exit）则是此次切入点所能直接到达的目的地址，此处所说的直接到达是指通过切入点路由表显示的目的地址。用符号A1表示初始切入点，从切入点A1的路由表中可以获取该主机所能达到的多个目标地址，假定分别为B1、B2、…、Bm。可以随机选取上述目标地址中的任意一个作为前进的方向（为了便于说明，在此选取B1作为前进目标），将前进信息和当前位置信息计入行动历史记录中，由此历史行动记录已经构成，记为H1。此时，H1=(A1，B1)。由于网络结构不同于标准迷宫，在任何一个节点，理论上均有多个可选方向（大于4个方向）作为下一步前进方向，因此需要构造一个行动方向可选记录集，记为 D1。此时，D1=(B2，B3，…，Bm)，在此未记录 B1是因为该节点已经被选择进行了渗透测试，所以不需要进行标记。当B1方向可达后，用网络侦听工具和网络攻击工具破解B1主机，以此获得该主机的最高权限。当上述目标均实现后，获取B1主机的路由信息表，假定路由信息表中显示的目标地址为 C1、C2、…、Cl。按照上述方法，随机选取上述目标地址中的任意一个作为前进的方向（为了便于说明，在此选取C1作为前进目标），将前进信息和当前位置信息计入行动历史记录中，此时历史行动记录 H1已经由 H1=(A1，B1)变更为 H1=(A1，B1，C1)。 与 此同时，行动方向可选记录集为(D1，D2)。

在此时，D2=(C2，C3， …，Cl)。 如果 C1点依然方向可达，且用网络侦听工具和网络攻击工具破解C1主机成功，以此获得该主机的最高权限后，依上述步骤继续进行渗透。如果在限定的时间内，C1无法完成上述操作，则利用类似迷宫路径算法的回退机制进行网络渗透回退，通过结合历史行动记录集H1和行动方向可选记录集(D1，D2)，确定回退后进行网络渗透的下一目标主机地址。由于网络中主机的安全性能、漏洞状态并不一致，且主机的口令、密钥强度存在明显的差别，所以只要同一网段中的一台主机存在安全隐患，均能完成对此网段上一级网络连接的渗透工作。利用此拓展的迷宫路径算法就完成了从初始切入点A1开始的最远目标地址渗透工作。由于整个网络拓扑结构不同于迷宫结构，网络中并不是任意两台主机之间都是彼此可达的。选择已经渗透成功的任意一台非A1主机作为初始切入点，重复利用上述网络渗透技术进行网络渗透，即可完成基于变更后的主机地址的网络渗透工作。利用这种拓展的迷宫路径算法，基本完成了整个网络拓扑的渗透遍历。

但是该算法存在一个明显的问题就是网络拓扑结构中的重复、无效信息过多，不利于后期进行网络攻击。以网络中任意一对网络主机为例，假定该成对网络主机分别为 A1、P1， 那么从 A1出发到达 P1的通路与从 P1出发到达A1的通路可能大相径庭。需要确定以哪一条通路作为行动路线。另外，在A1出发到达P1的通路或从P1出发到达A1的通路上，是否存在冗余路径也需要确定。只有将冗余路径删除并保留最短路径，在后期进行网络攻击时才能在最短时间内真正有效地达到所需的目的点。基于上述缺陷，利用图论中的相关理论与方法对拓展算法进行完善。通过这种方式将现实中的离散数据进行了数学意义上的整合处理。

2 基于图论算法的网络渗透完全图的生成

在图论理论中，有一个非常重要的思想就是极大连通子图的概念。用图论语言描述就是：设图G=(V，E)，其中变量V代表顶点集合，变量E代表边集合，变量G代表图。如果存在另外一个图 G1=(V1，E1)，其中变量 V1代表顶点集合，且 V1⊆V；变量 E1代表边集合，且 E1⊆E；变量G1代表图。若图G1中的任意两点之间是连通的，且图G1不存在回路，此时向图G1中添加任何一个顶点或边，图G1将出现回路或者变为非连通，那么图 G1就称为图G的极大连通子图。

按照上述理论，需要在此构造网络渗透图的极大连通子图，通过将若干个极大连通子图合并，来实现对网络渗透图的最小覆盖诉求。基于上述想法，首先对拓展算法进行改进。在每一步，完成对下一步主机的完全渗透工作后，记录从渗透成功节点到上一步节点的物理到达时间，以此时间作为该条通路的路径长度。假如当前地址是A1，而目标地址是B1，当成功获取B1的超级操作权限后，在B1主机上测试到达 A1主机的时长，以此作为通路A1B1的路径长度。用此方法，对成功获取权限后的主机进行路径长度测量，并将此信息记录在路径信息历史集合DI中。随着整个网络拓扑渗透的完成，得以获取所有可达路径的路径长度信息。利用获取的所有节点信息以及与之对应的节点间路径长度信息，重新构造一个图邻接矩阵，其具体表述如下：

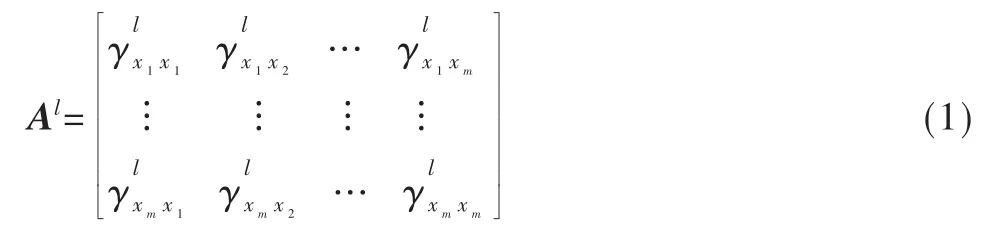
矩阵Al代表整个网络拓扑结构中的邻接矩阵，该矩阵中元素的排列顺序采用事先约定顺序（矩阵第一行从左至右依次代表节点x1，x2，…，xw；矩阵第一列从上至下依次代表节点，，…，）。 其中变量代表节点和x2直接可达的距离（此处所说的直接可达是指节点x2是节点x1直接子节点）。如果式(1)中的两节点之间直接不可达，则将其距离标记为∞。

式(1)对应的图为G=(V，E)。按照图论的算法，首先构造一个集合S={V0}，其中V0代表出发顶点。再构造一个集合T={除V0以外的顶点}。从式(1)中的矩阵中寻找与出发顶点V0最直接相邻的顶点，且其直接可达距离是直接相邻顶点中最小的，将此顶点标记为V1，并将其加入到集合S中。同时，修正式(1)中的距离值，如果加进 V1作为中间顶点，从 V0到其他顶点（不包括 V1）的距离小于现有距离，则修改式(1)中的距离值，否则不修改。重复上述步骤，直到集合S与集合T相等。

由此，对无效信息进行了过滤，找到了网络渗透的最短路径。

3 网络攻击分析研究与数据网络防护研究

上述内容对未知的网络拓扑进行了探索，明确了整个网络结构，并在此基础上完成了对网络拓扑的重点分析，找到了整个网络拓扑的最短路径，为下一步有针对性地进行防护网络攻击打下了坚实的基础。

针对上述分析中确定的整个网络拓扑结构中的最短路径，将最短路径中的每一个节点确定为关键节点。在具体的数据网络中，这些关键节点就是未来网络渗透和网络攻击的主要目标，对上述数据网络的关键节点主机，需要建立一台双备份服务器，该主机负责监控上述关键节点主机的动态信息。具体说来，就是在此服务器上，存储上述关键节点主机的IP地址及其对应的MAC地址，且形成一一对应的稳定关系。同时对整个网络中涉及上述关键节点主机的ARP请求进行实时监控，对于涉及关键节点主机发送的ARP请求，必须与服务器上的对应信息进行自动核对。一旦发现有与原地址不匹配的ARP请求发生，立即进行系统报警，同时定向跟踪此ARP请求发生的地址及时间。并将正确的ARP请求进行网络广播传送，以防止黑客行为的发生。所有关键节点主机要求变更地址的TCP/IP请求，必须提前通过手工报送的方式实现，不能采取自行更换主机网卡、主机IP地址的方式实现。同理，RARP请求的处理方式与上类似。

通过上述分析研究，对攻击网络进行数据分析，从任意出发点开始，设定下一步网络攻击的传播方向。设定的规则是根据当前节点与网络上任意可达节点之间的最短路径为其传播的具体路径。对网络中任意可达节点采取同样方法进行设定，并确定网络攻击的强度与时间，由此即可在制定的时间达到预期的网络攻击效果。

基于上述整体方法，任意网络拓扑结构下的网络渗透攻击均可确定。利用拓展的迷宫路径算法完成了对网络渗透的初步改善；在此基础上，利用图论相关理论与方法，最终完成了网络渗透攻击的全过程优化升级。通过确定的最短路径及关键节点，为数据网络中确立网络防御保护措施的实施范围、实施方式确定了明确的思路。

传统的网络渗透攻击研究在异构网络环境下的攻击研究不足，同时研究重心过多地侧重于被动防护研究，而对主动防御研究不足。从而导致网络安全研究一直处于被动挨打、疲于应对的局面。通过在网络渗透攻击研究中引入拓展的迷宫路径算法，为异构网络环境下的网络安全研究提供了主动应对策略与方法。本文通过引入拓展的迷宫路径算法，对任意复杂网络中的关键路径、关键节点进行网络安全策略分析、防护，从而为解决整个网络安全问题提供了切实可行的解决方案。

[1]HAMISI N Y，MVUNGI N H，MFINANGA D A，et al.Intrussion detection by penetration test in an organization network[J].Adaptive Science&Technology，2009：226-231.

[2]肖竟华，王熠.基于攻击模式的攻击图自动生成方法研究[J].计算机安全，2008(7)：23-25.

[3]宋舜宏，陆余良，夏阳，等.基于贪心策略的网络攻击图生成方法[J].计算机工程，2011，37(2)：126-128.

[4]崔颖，章丽娟，吴灏.基于攻击图的渗透测试方案自动生成方法[J].计算机应用，2010(8)：2146-2150.

[5]金晶，孙东来，陈秀真.基于攻击图及蚁群算法的安全评估[J].信息安全与通信保密，2009(4)：79-81.

[6]祝宁，陈性元，王前.基于效果的网络攻击分类方法[J].计算机应用，2006(S1)：162-164.

[7]叶云，徐锡山，贾焰，等.基于攻击图的网络安全概率计算方法[J].计算机学报，2010，33(10)：164-167.