视频显示器四基色有序平滑显示算法研究

吴伟琦

(1．广西工业职业技术学院建筑工程系, 中国 南宁 530001；2．桂林师范高等专科学校数学与计算机科学系,中国 桂林 541001；3．百色学院科研处，中国 百色 533000)

在计算机视频监示器和电视机视频显示中的色彩是通过红(R)、绿(G)、蓝(B)3种基色来具体体现的，每种基色各有0～255共256种色阶，3种基色的色阶的每种组合代表一种颜色，改变视频监视器中某个颜色寄存器的值,在监视器中即可产生出相应的可显示颜色.

随着视频显示技术的不断发展,视频显示器上所能显示的颜色也将会越来越多,基色的种数也将不局限于3种,各种基色的色阶的取值范围也将不局限在0～255之间.

文献[1]讨论了三基色的色彩的有序平滑显示算法,且只研究了每种基色取值范围都是0～255的情形，文献[2]讨论了三基色的基色色阶的取值范围不同时的有序平滑显示算法．本文利用图论的方法从理论上讨论基色种数为4种且每种基色的色阶取值范围不同的情形下的有序平滑显示算法.

1 基本概念

类似于文献[1]给出下列基本概念：

定义1称C(g1,g2,g3,g4)为色彩函数，其中g1,g2,g3,g4为色彩的4种基色的色阶,C(g1,g2,g3,g4)是由4种基色G1,G2,G3,G4的取值组合成的色彩值. 称C(g1,g2,g3,g4)组成的集合为色彩集,记作

C={C(g1,g2,g3,g4)|0≤gj≤rj,(gj,rj是正整数,j=1,2,3,4)}.

定义2对于色彩集C中的任意两个不同的元素Cx=Cx(g1x,g2x,g3x,g4x)和Cy=Cy(g1y,g2y,g3y,g4y),定义函数关系：Φ(Cx,Cy)=|g1x-g1y|+|g2x-g2y|+|g3x-g3y|+|g4x-g4y|,若Φ(Cx,Cy)=1,则称色彩值Cx和Cy是1-相邻的, 此时称Φ为色彩值1-相邻规则.

对于色彩集C,根据色彩值1-相邻规则,可以构造一个色彩值1-相邻点对集：

D(C)={(Cx,Cy)|Cx,Cy∈C,且Cx≠Cy,Φ(Cx,Cy)=1}.

定义3对于任意的Cx,Cy∈D(C),构造一条边连结Cx,Cy两点,记为e(Cx,Cy),称e(Cx,Cy)为色彩值1-相邻规则Φ下的色彩相邻边.

显然,所有色彩相邻边e(Cx,Cy)可构成一集合,记为E,即E={e(Cx,Cy)|Cx,Cy∈D(C)且Cx≠Cy}.

由以上三定义,可得到一种特殊的图的定义.

定义4由色彩集C,色彩相邻边集E以及色彩值1-相邻规则Φ构成的三元有序数组G=(C,E,Φ)称为基于G1,G2,G3,G4的四基色的色彩图,简称色彩图.

显然，以上定义的色彩图与图论中图的概念是完全一致的，相应的色彩显示问题就转换成了图论上著名的Hamilton圈存在性问题，也即在色彩图上是否存在Hamilton圈. 于是，对于以上定义的色彩图,若在其上存在Hamilton圈，则存在一个全部色彩的计算机平滑循环显示算法.

本文以G1,G2,G3,G4为坐标轴构造四维空间坐标系,设g1,g2,g3,g4的取值范围分别为: 0≤gj≤rj,(j=1,2,3,4),由此构造一个四维立方体,对该立方体施以长为1的划分,则可形成一个四维立体图G,由于色彩函数值C(g1,g2,g3,g4)与四基色G1,G2,G3,G4的取值是一一对应的,于是可将四维立方体上的点(g1,g2,g3,g4),(0≤gj≤rj,j=1,2,3,4),与色彩值C(g1,g2,g3,g4)相对应,显然,四维立方体图G与色彩图是同构的,从而讨论色彩图的Hamilton圈的存在性,只需讨论四维立方体图G的Hamilton圈的存在性.

2 主要结果及证明

引理1[3]一个简单无向图为偶图的充要条件是不含奇圈.

引理2[3]若G是Hamilton图,则对V(G)的每个非空真子集S,均有ω(G-S)≤|S|. 其中ω(G-S)是图(G-S)的连通分支数.

定理1设四维立方体图G=(C,E,Φ)中的顶点(g1,g2,g3,g4)各分量的取值范围为: (0≤gj≤rj,j=1,2,3,4),则G存在Hamilton圈的充要条件是r1,r2,r3,r4中至少有一个为奇数.

证必要性的证明，因为四维立方体图G=(C,E,Φ)的顶点数等于(r1+1)(r2+1) (r3+1)(r4+1). 如果所有rj(j=1,2,3,4)为偶数,则(r1+1)(r2+1) (r3+1)(r4+1) 为奇数.又由于四维立方体图G=(C,E,Φ)不存在奇圈,所以由引理3.1知它是偶图,设此偶图的二分类为{S1,S2},因|S1|+|S2|=(r1+1)(r2+1) (r3+1)(r4+1) 为奇数,于是不妨设|S1|>|S2|,由偶图的性质知G-S2=S1是G的独立集,所以ω(G-S2)=|S1|>|S2|,根据引理3.2,四维立方体图G=(C,E,Φ)不是Hamilton图.

充分性的证明,若ri(i=1,2,3,4)中至少有一个为奇数,不妨设r3是奇数,此时只需在四维立方体图G中找出一个Hamilton圈即可.现将G的顶点列成表1.

表1 四维立方体图G的顶点

续表

续表

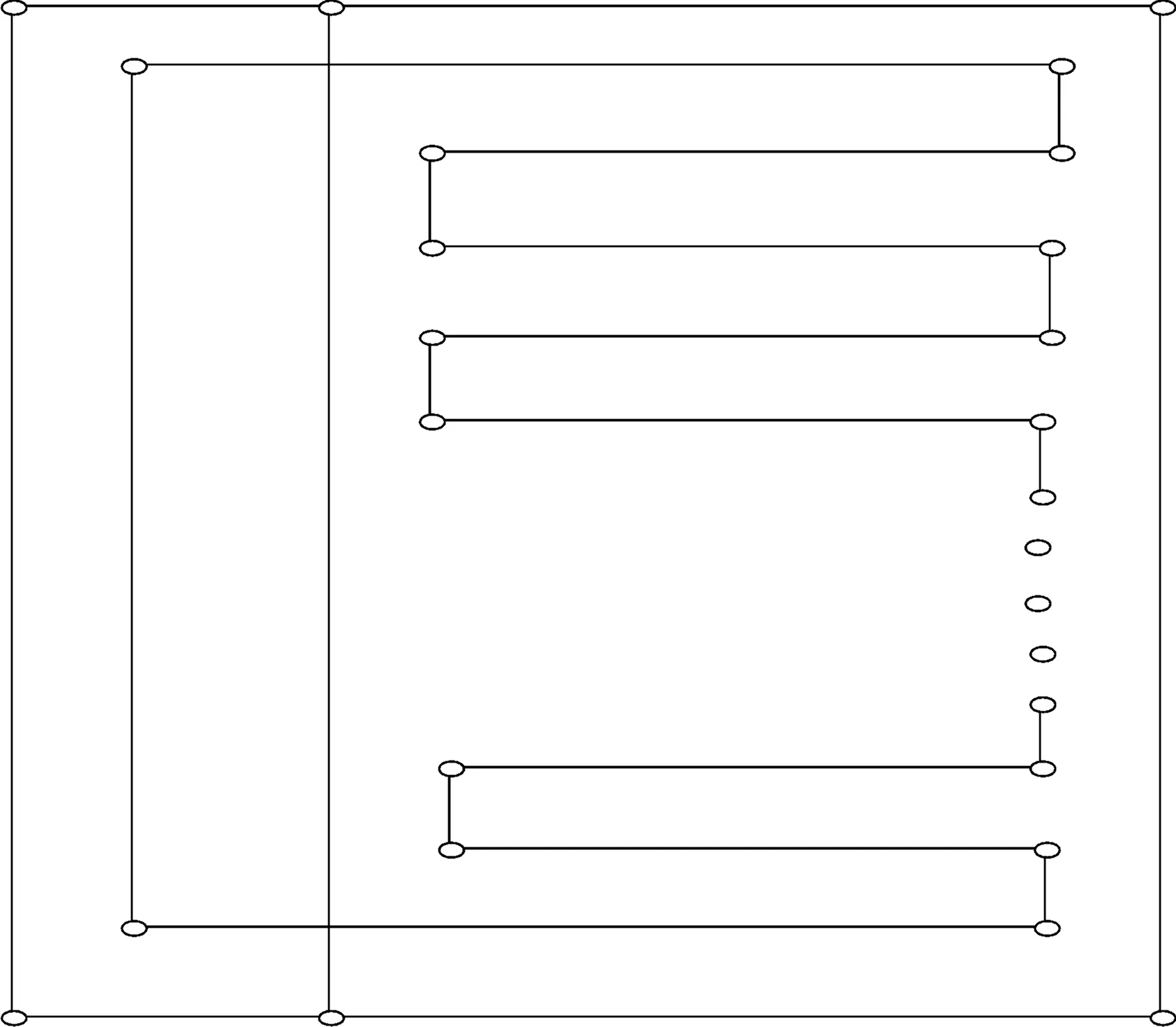
图1 G中的一个Hamilton圈示意图

显然,表中任意相邻的两个顶点在图G中也是相邻的.因为r3是奇数,所以表1排列的顶点共有偶数行,于是易找出四维立方体图G的Hamilton圈,例如,如图1所示的连接方式就构成四维立方体图G中的一个Hamilton圈.

推论1[1]三维“格子笼”图G=(V,E),其中

V={(r,g,b)|0≤r,g,b≤n且r,g,b和n是整数,n≥1}

E={((rx,gx,bx),(ry,gy,by))||rx-ry|+|gx-gy|+|bx-by|=1}

则图G存在Hamilton圈的充要条件是n为奇数.

推论2[2]设三维“格子笼”图G=(V,E)，其中

V={(r,g,b)|0≤r≤n1,0≤g≤n2,0≤b≤n3且r,g,b和ni是整数,ni>1(i=1,2,3)},

E={((rx,gx,bx),(ry,gy,by))||rx-ry|+|gx-gy|+|bx-by|=1}.

则图G存在Hamilton圈的充要条件是ni(i=1,2,3)中至少有一个为奇数.

3 结束语

显示技术从最初的单基色显示、双基色显示到现今普遍使用的三基色显示，且随着科学技术的发展而不断提高．目前对多基色显示技术也在广泛讨论和研究，像四基色，六基色的LED显示已开始应用了，本文讨论的四基色平滑显示算法为多基色技术提供了一个平滑显示的理论依据．

参考文献：

[1] 郭常忠, 王 敏. 一种基于RGB三基色的计算机色彩的有序显示算法[J]. 计算机研究与发展, 1997, 34(4): 312-315.

[2] 李 政, 王 敏.“格子笼”图的Hamilton圈问题[J]. 大学数学, 2007, 23(1): 147-150.

[3] BONDY J A, MURTY U S. Graph theory with applications[M]. London: Mac Millan Press, 1976.

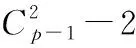
[5] 唐干武, 唐高华, 王 敏. Erdös-Sos猜想的一个结果[J]. 西南师范大学自然科学学报, 2009, 34(1): 24-27.

[6] WANG M, FANG X G. Parking a pair of graphs {(p,p-1),(p,p)} and slater’s problems[J]. J Chinese Syst Sci Math Sci, 1989, 9(2): 133-137.

[7] 唐干武，王 敏.包装(p,p-2)图和不含K3的(p,p+1)图[J]. 江西师范大学自然科学学报,2005, 29(3): 220-223.

[8] YIN J H, LI J S. The Erdös-Sòs conjecture for graphs whose complements contain noC4[J]. Acta Math Appl Sinica, 2004, 20(3): 397-400.

[9] WANG M, LI G J. On the a tree of orderpwith a (p,p+1)-graph[J]. J Syst Sci Comp, 2003, 16(1): 122-132.

[10] 方新贵, 王 敏. 包装{(p,p-1),(p,p)}图对和Slater问题[J]. 系统科学与数学, 1989, 9(2): 133-137.

[11] 唐干武, 王 敏. 一类图的哈密顿分类[J]. 纯粹数学与应用数学, 2009, 4(25): 711-715.

[12] 张智勇, 张远平. 一些具有非固定步循环图中生成树的个数[J]. 湖南师范大学自然科学学报, 2007, 30(3): 18-21.