手机振动影响及模式优化设计研究
叶南阳
(北京邮电大学信息与通信工程学院,中国 北京 100876)
目前手机的振动功能已经应用于人们的生活,然而人们对于手机的振动原理以及手机振动可能对手机及其使用者的影响了解得较少,过去的研究中,很少涉及手机振动模式及其影响.
通过对手机的振动模式进行深入的研究分析和有限元仿真,从理论上分析手机的不同模式对手机和环境产生的影响.并设计几种较为合理高效的手机振动模式,可以减少手机振动对手机和人体的影响[1],并降低了振动能耗.
1 振源振动原理分析

图1 偏心轮
首先建立手机振动模型,得出了手机振动振源参数对振动效果的影响.为了使结果具有普遍性,理论分析采用了圆形偏心轮的振动器件为研究对象.如图1所示.
根据转动惯量计算公式可知,该模型与在轴上偏心安装了高比重合金旋转振动的模型等效,因此具有普适性.当偏心轮开始转动时,偏心轮的质心作圆周运动,由动量定理,手机其他部分质心相反方向运动,其质心振动频率逐渐升高直至到达偏心轮振动频率后开始稳定振动.
振动稳定时,振动器件受重力和支持力的作用,二者的作用力大小相等,方向相反,可不考虑重力及支持力.此时振动相当于完全非弹性碰撞,由实验知,振源能量一部分转化为振动能量,另一部分转化为声波能量,极少部分能量转化为热能,在分析中忽略不计. 由能量守恒可得:
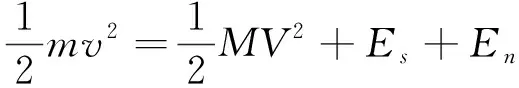
式中M表示手机除振源外部分质量;V表示除振源外部分振动速度;Es表示声波能量;En表示器件不规则振动的能量即手机的其他部分会发生微小形变时产生的能量.
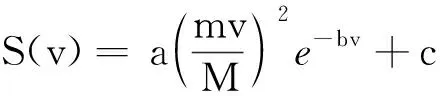
2 噪声波谱傅里叶分析
振动过程中,单次振动时间设为Δt,振动周期为T,对振动能量函数作Fourier变换. 如图2所示.
由计算可得噪声的频谱密度函数[2]为

由图2可知,噪声能量集中于低频段,在次声波段,能量有较大比例,危害人体健康[1],低频噪声与手机部件固有频率相近,产生共振,损坏部件.必须减少噪声能量,同时又减小噪声在次声段的比例.
3 振动能量分析及有限元仿真
下面用场的观点分析手机振动模型,得出手机的振动能量分布函数,并由方程建立能量有限元仿真模型并得出能量分布.
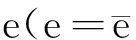
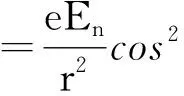
由第一类曲面积分可得通过曲面ax+by+cy=0的能量[4]为

(1)
在式(1)中取e=0.13,使用Femap软件并利用文献[5]中方法进行动态有限元仿真[6],可得振动时手机中的能量分布即载荷强度分布[7].如图3所示.将(1)式化简可得:一个振动周期内通过平面的能量为[8]
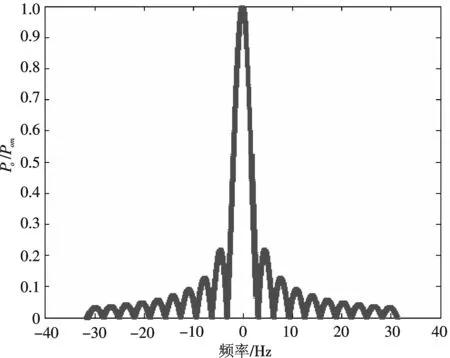
图2 噪声波谱图

水平方向振动 竖直方向振动图3 有限元仿真手机振动的能量分布
以参数表(见表1)中最低转动速率为例,由有限元仿真可得,在振动过程中,当转子向水平方向运动时,机体的最大形变量为4.01 μm,增加振动频率时,通过仿真,采用了改进的插值节点提高精度[9],并使用MATLAB对图像进行了降噪[10].可得随转子的振动频率逐渐远离手机振动固有频率,最大形变量减小,两振动去耦[11],次声波噪声的能量减小振动耗能却大幅增加,下面求最优解.
4 结论
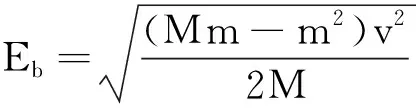
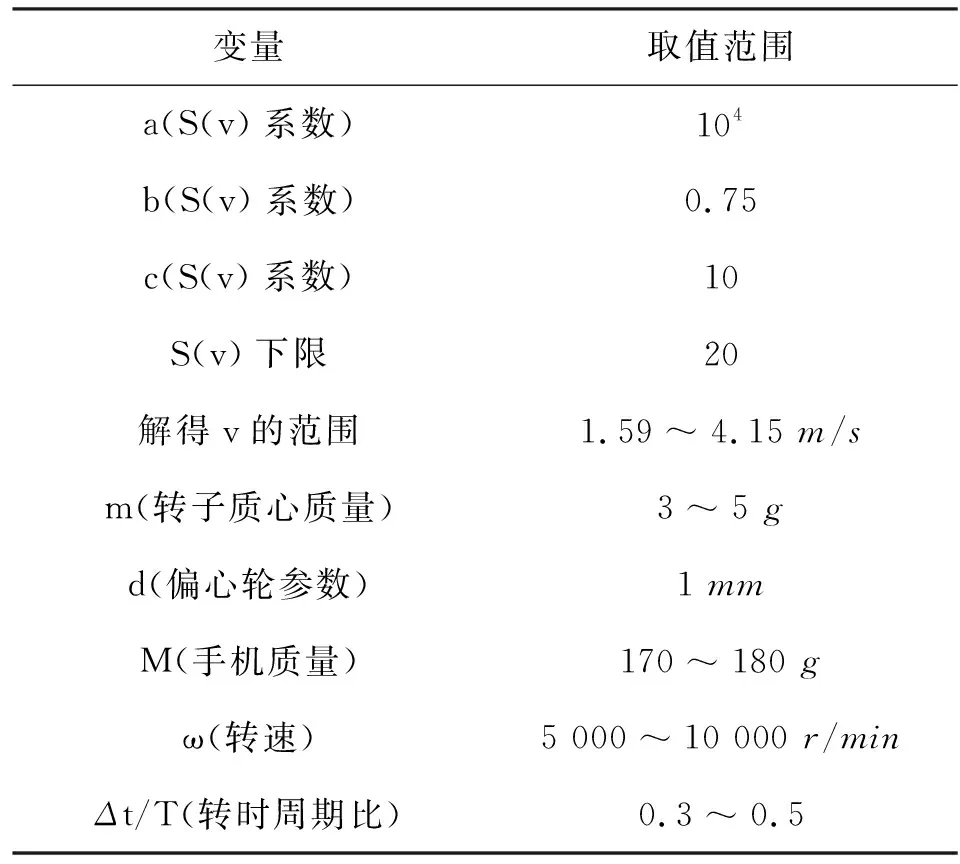
表1 模型参数表
求解方程为多变量非线性优化问题,取各个函数的权值相同组成适应性检验函数[12],用遗传算法MATLAB程序[13-14]对模型进行数值求解可得m=3.13 g,M=170.5 g,w=6 307 r/min,Δt/T=0.45.
5 结语
本文对手机的振动原理进行了深入研究,并优化求解了振动能耗问题和噪声问题,并通过建立手机振动模型的方法,得出了振动最佳模式.该模式能降低手机的振动能耗,减少对人体的危害.
参考文献:
[1] 赵选科,王莲芬,何俊发.次声波及次声武器[J].大学物理,2005,24(5):57-59.
[2] 王 凯,李 言,郑建明,等.用复函数快速傅里叶变换相位谱分析转子偏心运动成因[J].制造技术与机床,2004,10(2):58-60.
[3] 刘裕勤,管 立.关于振动势能的计算[J].工科物理,1999,9(2):39,28.
[4] 赵凯华,罗蔚茵.新概念物理教程——力学[M].北京:高等教育出版社,2005.
[5] 蔡忠云,唐文勇,张圣坤.能量有限元方法在复合材料层合梁耦合结构振动分析中的应用[J].振动与冲击,2010,29(10):26-27.
[6] 罗 旭.Femap & Nx Nastran基础及高级应用[M].北京:清华大学出版社,2009.
[7] 梁国平.有限元程序自动生成系统及有限元语言[J].力学进展,1990,20(2):200-201.
[8] 郭玉翠.数学物理方法[M].大连:大连理工大学出版社,2010.
[9] 王爱民,王勖成.有限元计算中疏密网格间过渡单元的构造[J].清华大学学报,1999,39(8):100-103.
[10] 包宋健,许艳英,陈帅华,等.MATLAB语言在数字图像处理中的应用[J].工业控制计算机,2011,24(6):38-39.
[11] 张三慧.大学物理学(第4册):波动与光学[M].北京:清华大学出版社,2000.
[12] 周建兴.MATLAB从入门到精通[M].北京:人民邮电出版社,2010.
[13] 鲍祖尚,胡潇潇.流变阻尼器减震控制算法设计[J].湖南师范大学自然科学学报,2011,34(6):31-34.
[14] 雷英杰,张善明,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.

