Bayes线性无偏估计的稳健性

邱红兵, 罗季, 孙旭

(1. 广东工业大学应用数学系,广东 广州 510006； 2. 浙江财经学院数学与统计学院, 浙江 杭州 310018；3. 东北财经大学统计学院, 辽宁 大连 116025)

0 引 言

考虑线性模型y=Xβ+ε

(1)

在线性模型(1)式中,设参数向量β有先验分布π:Eβ=μ,Cov(β)=V

(2)

R(d,β)=E[L(d,β)],

这里及以下E均表示关于y和β的联合分布求均值.

(3)

(4)

其中二次损失函数为L(d,β)=(d-β)′(d-β)

(5)

这方面的文献可参见文献[1-3]. 利用可逆矩阵的逆矩阵公式：

(T+XVX′)-1=T-1-T-1X(V-1+X′V-1X)-1X′T-1

回归系数β的贝叶斯线性无偏估计也可表为

(6)

在线性模型的参数估计中,总是首先假设D(ε)∈R(0,T),但在实际问题中,随机误差分布中的均值与协方差矩阵可能略有偏离,因此我们希望据此所做出的统计推断关于误差分布具有稳健性. 对于线性模型(1)式,关于回归系数β及可估函数C′β的估计的稳健性研究, 文献[4-7]中在二次损失及矩阵损失下分别研究了回归系数β及可估函数C′β的最小二乘估计,广义最小二乘估计, Gauss-Markov估计的优良性,并对Gauss-Markov定理作了推广,得到了推广的Gauss-Markov定理成立的误差分布的最大类. 对于线性模型(1)式中参数的Bayes估计的稳健性, 韦来生在文献[8]中在二次损失下考虑了错误先验假设下回归系数贝叶斯线性无偏估计的小样本性质； 文献[9]中在MSEM准则、PRPC准则以及PPC准则下讨论了Bayes线性无偏估计相对广义线性无偏估计的优良性；文献[10]中则讨论了错误先验假定下贝叶斯线性无偏估计的稳健问题. 而对于Bayes线性无偏估计关于误差分布的稳健性,尚很少见到相关文献.

定义1对于线性模型(1)式, 在先验分布(2)式下, 给定β的估计类(μ)及误差项ε的一类分布R(η,Σ),若d*∈(μ),使得R(d*,β)≤R(d,β),

对所有d∈(μ)及D(ε)∈R(η,Σ)成立,则称β的估计d*是[V,(μ),R(η,Σ)]最优的.

1 Bayes线性无偏估计关于误差分布的稳健性

引理1[2]设Eε=η,Cov(ε)=W,D∈Rn×n,则有E(ε′Dε)=η′Dη+tr(DW).

tr(AX-I)′(AX-I)V+trA′AΣ+η′A′Aη.

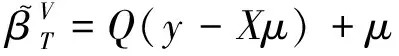
记A-Q=P,利用QXVX′=VX′-QT,可得

(7)

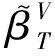
(8)

即对任意P∈Rp×n,有

2tr[Q(Σ-T+ηη′)P′]+tr[P(Σ+XVX′+ηη′)P′]≥0

(9)

因Σ+XVX′+ηη′≠0,则存在L∈Rp×n,使得tr[L(Σ+XVX′+ηη′)L′]>0.若(Σ+ηη′)T-1X≠X, 等价于Q(Σ-T+ηη′)≠0, 则取P=kL代入不等式(9)式, 得

2ktr[Q(Σ-T+ηη′)L′]+k2tr[L(Σ+XVX′+ηη′)L′]≥0

(10)

2ktr[Q(Σ-T+ηη′)L′]+k2tr[L(Σ+XVX′+ηη′)L′]<0

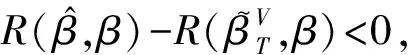
充分性：若(Σ+ηη′)T-1X=X,等价于Q(Σ-T+ηη′)=0, 则对任意P∈Rp×n, 由(7)式有

定理2给定估计类(μ),令

定理2的证明给定估计类(μ),D(ε)∈R(T),则显然有(Σ+ηη′)T-1X=X,于是由定理1知是[V,(μ),R(0,Σ)]最优的.

Σ+ηη′=DD′=XΛX′+TZB′X′+XBZ′T+TZWZ′T,

定理得证.

2 一些推论

由定理1及定理2,容易得到下列推论.

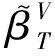
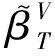
推论4给定估计类(μ),令

对于线性模型(1)式,若D(ε)∈R(0,I),且β的先验分布(2)式中V=Ip,即先验分布为π：

Eβ=μ,Cov(β)=I.

推论7给定估计类(μ),令

推论8给定估计类(μ),令则R0(I)是使得β的估计是[I,(μ),R(0,Σ)]最优的误差项ε的最大分布类.

[1] Trenkler G, Wei L S. The Bayes estimator in a misspecified regression mode1[J].Test, 1996(5)：113-123.

[2] Wang S G, Chow S C. Advanced linearmodel and applications[M].New York:Marcel Dekker,1994.

[3] 张伟平. 贝叶斯线性无偏估计[D]. 合肥:中国科技大学, 2005.

[4] Kariya T,Kurata H. A maximal extension of the Guass-Markov theorem and its nonlinear version[J].J Multivariate Anal, 2002, 83：37-55.

[5] 刘湘蓉. 最小二乘估计关于误差分布的稳健性[J]. 应用概率统计, 2006, 22(4)：429-437.

[6] 邱红兵, 罗季.线性模型中广义最小二乘估计关于误差分布的稳健性[J]. 吉林大学学报:理学版, 2009, 47(1)：13-16.

[7] 邱红兵, 罗季.Gauss-Markov估计关于误差分布的稳健性[J]. 应用概率统计, 2010, 26(6)：615-622.

[8] 韦来生. 错误先验假定下回归系数Bayes估计的小样本性质[J]. 应用概率统计, 2000, 6(1)：71-80.

[9] 霍涉云, 张伟平, 韦来生. 一类线性模型参数的Bayes估计及其优良性[J]. 中国科学技术大学学报, 2007, 37(7)：773-776.

[10] 张伟平, 韦来生. 错误先验假设下Bayes线性无偏估计的稳健性[J]. 应用概率统计, 2007, 23(1)：59-67.