物流网络中分布式OD运载需求的分时段限流优化
胡少龙, 胡志华,2
(1.上海海事大学 物流研究中心, 上海 201306) (2.同济大学 经济与管理学院, 上海 200092)
物流活动离不开交通工具的使用,交通网的新建和交通工具的大量使用增强了企业或区域的物流能力,提高了全社会的物流速度,但随之也引发了交通拥堵、交通事故和交通环境污染等问题.环境承载力(environment carrying capacity, ECC)被定义为某一环境状态和结构在不发生对人类生存发展有害变化的前提下,对所能承受的人类社会作用在规模、强度和速度上的限制,是环境基本属性有限的自我调节能力的量度[1].运输过程中产生了噪音污染和大气污染.其中,汽车尾气对大气环境的毒害众所皆知,尾气污染一旦超过其所在区域的环境承载力,将使城市空气长期处于污染状态.
国外绿色物流研究开始较早,应用广泛[2-4].如文献[5]研究绿色物流的重要性、绿色物流水平、绿色物流动机和障碍;文献[6]通过建立多目标优化模型研究CO2排放对基础设施成本的影响,并将环境影响作为优先考虑的目标;文献[7]运用EOQ模型研究在3种不同供应链环境下,考虑碳排放的生产和运输策略.各领域学者对新能源汽车的研究和政策的支持,使绿色运输真正成为可能.我国在绿色物流研究方面近年来成果颇丰,文献[8]通过建构评估模式对绿色物流发展关键因素进行分析,并运用图论与矩阵工具找出绿色物流的中心问题,为绿色物流发展提供了科学的决策依据;文献[9]从绿色物流的内涵及特点入手,阐释发展绿色物流的必要性,分析我国发展绿色物流存在的障碍,提出我国绿色物流发展的对策.在OD运载网络研究方面,文献[10]研究了未来交通条件对路径选择行为的影响;文献[11]在公路网络中OD流旅行矩阵和路径识别的研究中提出优化交通板位置扫描;文献[12]考虑到动态分配矩阵的影响以及用户对交通拥堵的反应,研究动态OD流的需求估算的柱生成算法.
1 问题
在路段无容量限制、没有对车辆进行分时限流的情况下,运输需求都会采用最短路径进行运输,这种运载网络的总运输距离最小,即总的尾气排放量也最小,但会增加某些路段高峰时的承载量,使它们长期处于较严重的污染状态,进而影响路段周围居民的生活和出行.将具有起点和目标点的运输需求统称为OD(origin and destination)运输需求.采用分时段限流计划后,承载量达到某个上限的路段将被“关闭”,剩余的OD流量将重新选择路径运输.这种策略可以将尾气污染控制在环境自我调节量度之内,降低总污染效用.
在实际生活中,货物运输主要安排在晚间,但各需求点在白天时段会有紧急需求.基于以上分析,提出对道路进行分时段限流计划,将一天划分为白天(7~22时)和晚上(23~次日6时)2个时段,并限定这2个时段OD流的通行量,以达到以下目标:① 满足各需求点紧急需求;② 降低道路交通拥挤程度,同时降低污染产生量;③ 使道路之间的OD承载量均衡.
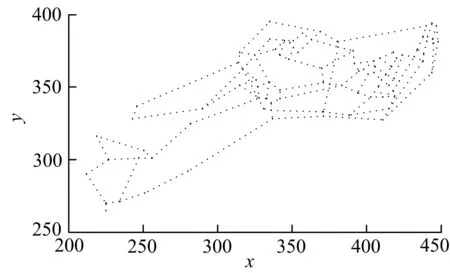
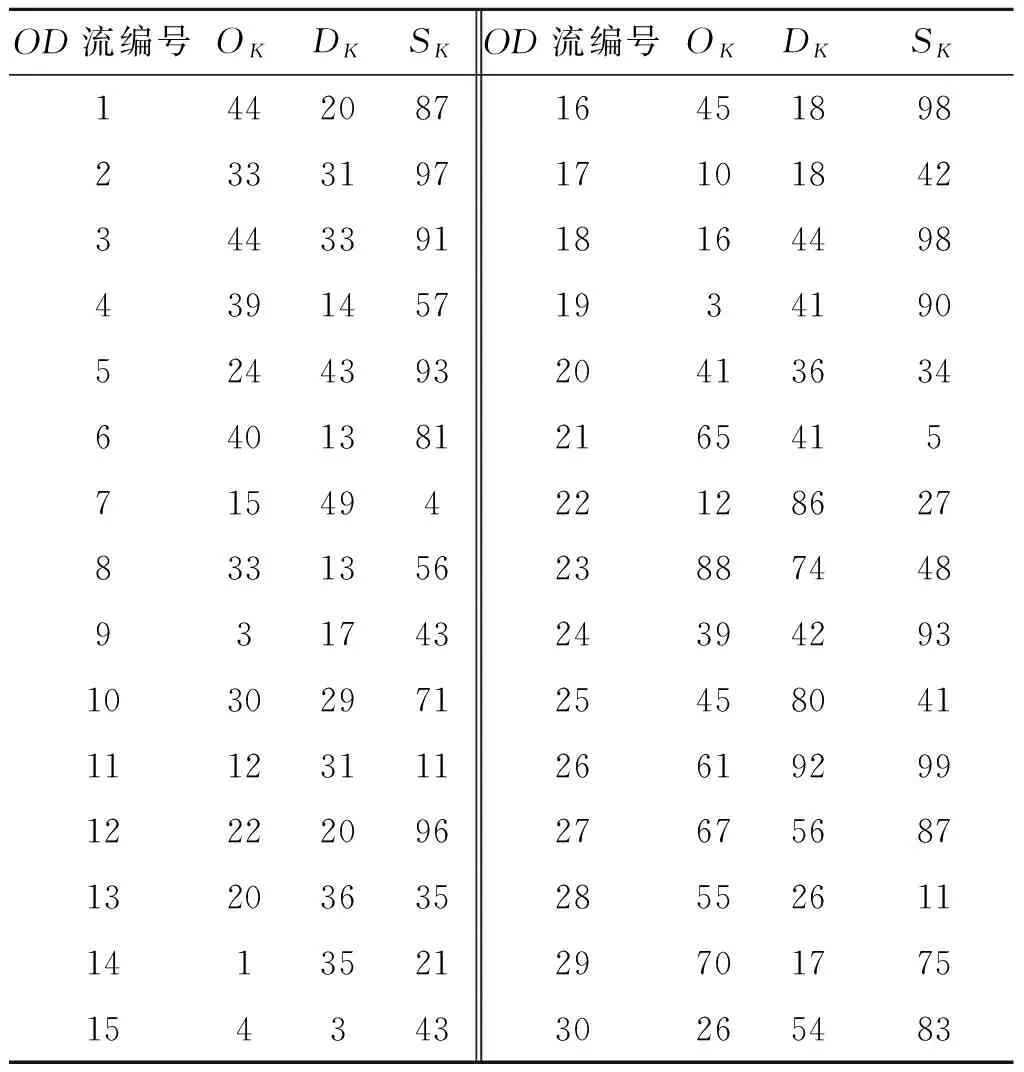
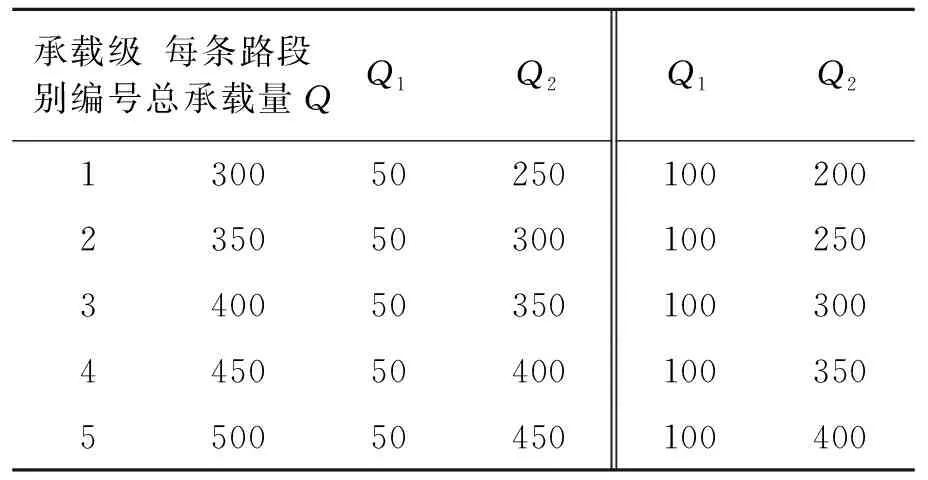
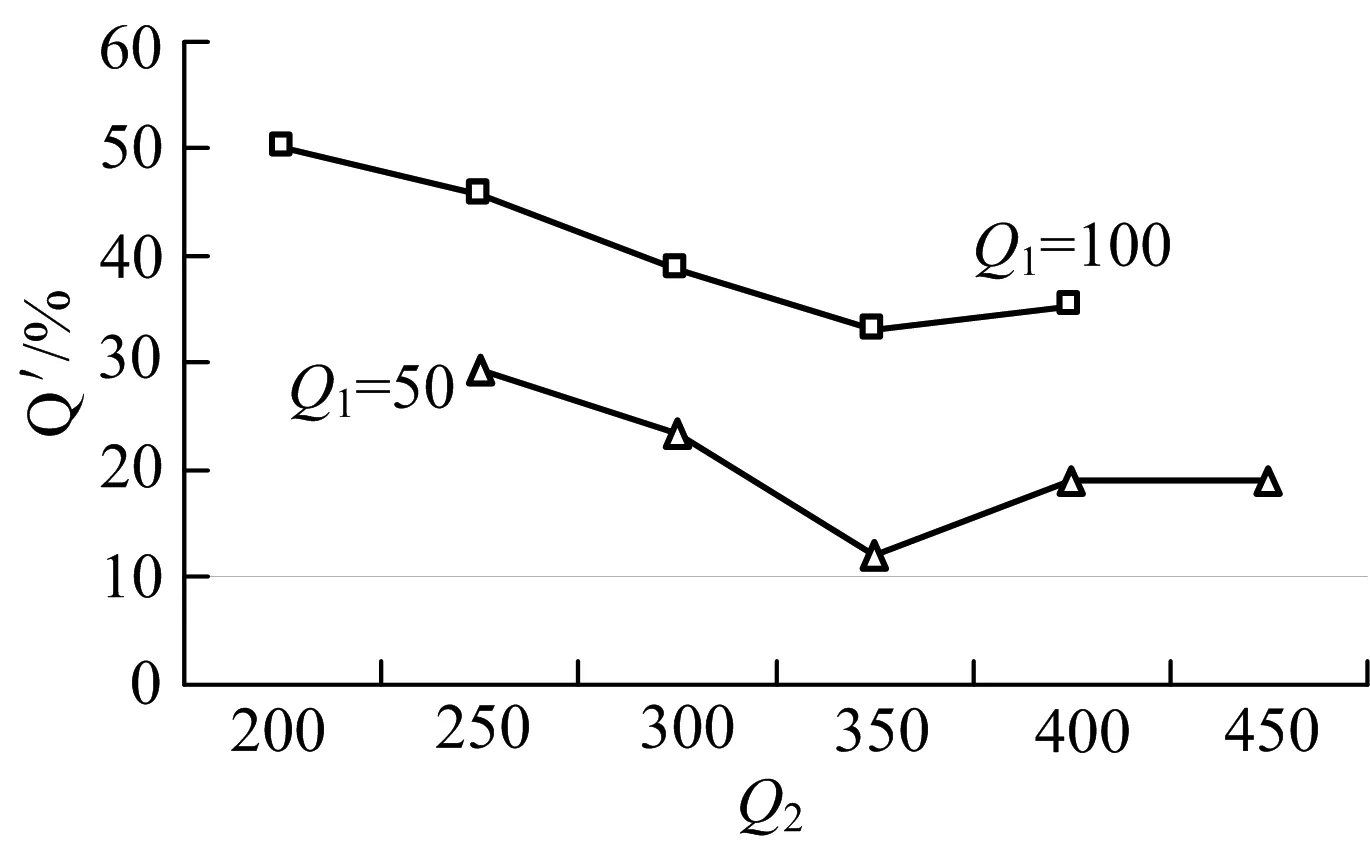
对模型中参数路段承载量上限的设置参考文献[13]中对汽车尾气初期扩散与扩散参数的研究.根据尾气排放量扩散与时间的关系,对每1.5 min,选取扩散参数y=k·xb(选取文献中参数计算值与参数现场示踪值误差最小的参数配比,即k=0.215,b=0.88).由上式可知,路段承载量越大,扩散时间越长.由于0 OD运载需求由起点O、目标点D和流量大小定义.对区域内的多个运载需求,基于最短路径模型建立多OD的整数规划模型,目标是使总运输距离最小化.并且,规定流量为类似集卡的单位流;单位距离运输成本相等;司机完全按照最短路径驾驶. 1) 相关集合与参数 ①N:所有路口节点的集合,i,j∈N均表示其中的节点;②OD:OD流集合,k∈OD表示其中的特定OD流;③Ok:OD流k的起点;④Dk:OD流k的终点;⑤Sk:OD流k∈OD需要从起点Ok向终点Dk运输的货物量;⑥Ri,j:表示邻接矩阵,若Ri,j=1,则i,j∈N两点直接相连;否则Ri,j=0;⑦Ci,j:表示任意i,j∈N两点之间的距离. 2) 决策变量 xi,j,k:表示路段i→j需要承载OD流k∈OD的运输量. 3) 目标函数 对多OD流最短路径的建模和路段承载量的研究,以总运输距离最小化为目标: (1) 4) 约束函数 (2) (3) xj,i,k)=0 (4) ∀i∈N,k∈OD:xi,Ok,k=0 (5) ∀j∈N,k∈OD:xDk,j,k=0 (6) 式(2)限定任意OD流k∈OD的起点Ok的货物发送量等于终点Dk的需求量.式(3)限定任意OD流k∈OD抵达终点Dk的运输量等于其需求量.式(4)限定任意OD流k∈OD经过的路段净流量等于零.式(5)和式(6)是对OD流起点和终点的限定,其移动路径的限制有:① 不能从其他节点向开始节点反向流动;② 不能从终止节点向其他节点反向流动. 为了研究分时段限流计划对总运输距离和各路段承载量变化的影响程度,基于2.1节中模型,增加时段维度,并限定每条路段在各时段的承载量,建立如下的多OD流分时段限流模型. 1) 相关集合与参数 在2.1节所提模型的集合与参数的基础下,增加一个时段集合和路段在每个时段的承载量参数;①T:时段集合,设T={1,2},其中1表示7~22时,2表示23~次日6时;②Qt:表示路段在时段t∈T内OD流承载量. 2) 决策变量 增加时段维度后,定义xi,j,k,t表示路段i→j在时段t∈T内承载OD流k∈OD的运输量. 3) 目标函数和约束函数 将重新定义后的决策变量替换第2.1节中模型的决策变量,并增加约束函数式(7),目的是限制不同时段内路段的承载量,目标函数仍然是使完成所有OD流运输量条件下总运输距离最小.由于OD流有方向,而路段无向,所以用(xi,j,k,t+xj,i,k,t)表示所有通过路段i↔j上的运输量. (7) 考虑N=92个节点的物流管理,节点坐标(x,y)分布如图1,各节点之间直接相连的路段有140条,另设置30条已知起点O和终点D(均通过U(1,92)生成)和运输量(通过U(1,100)生成)大小的OD流,具体如表1.路段在各时段的承载量Q的设置如表2. 图1 各节点之间的联通情况 为了方便对求解结果的分析与可视化,采用以下方法对第2.2节提出的模型中的决策变量进行降维处理.对第2.1节中模型的三维变量的降维处理可采用相同的方法转化,这里不再阐述. 表1 OD流相关参数设置 表2各时段路段承载量 Table2Roadcarryingcapacityofeachtirneperiods 承载级别编号每条路段总承载量QQ1Q2Q1Q2 130050250100200 235050300100250 340050350100300 445050400100350 550050450100400 1) 集合定义 ①E:表示路段集合E={1,…,140},e∈E表示任意路段编号; 2) 决策变量 3) 约束函数 约束函数式(8,9)将四维决策变量转换为二维决策变量. (8) (9) 根据3.1中参数的设置和对决策变量的降维处理,对模型进行求解并将决策变量转化为二维.以不限定路段承载量条件下白天时段(共16 h)总OD流运输量为基准,用式(10)比较采用分时段限流计划后白天(7~22时)时段总OD流的运输量之间的差异.从图2中可以很明显地得出以下结论:① 当Q1一定时,随着Q2的增大,白天时段的承载量先减少,后趋于平缓.出现这种现象的原因是,随着Q2的增大,白天时段没有按照最短路径运输的那一部分OD流转移到了夜晚运输;② 当Q2一定时,随着Q1的增大,白天时段的承载量均出现上升.出现这种现象的原因正好与上面相反. (10) 图2 限流与不限流白天通行量比较 Fig.2Comparedaycarryingcapacitybetween limitandunlimttransportflows 如图3,若不限制路段承载量,需要总共80条路段来承载本节所设置的30条OD流运输量,各路段之间的承载量会出现较大波动,其中最多的是第65号路段需要承载502个单位的运输量,而最少的第8号和12号路段需要承载的运输量只有4个单位.所以如果第65号路段长期承载大运输量,就可能造成该路段的交通拥堵,尾气和噪声污染超出环境承载力,给路段周围居民的出行和生活造成长期影响.采用分时段分流计划后,各路段承载量的波动大幅减小.承载30条OD流运输量的路段增加到93条,路段之间承载量波动大幅度缩小. a) 不限流量 b) 限载量Q=300 Fig.3Roadcarryingcapacityfluctuatedunderlinit andunlimttransportflow 基于以上分析,对不同流量限制前后各路段承载量的变化进一步分析.以不限流条件下各路段承载量为基数,分别求解路段总承载量Q=300,400和450时,各承载量减少的路段(中心路段)的下降幅度ΔQ.由图4可知,随着对路段承载量上限的逐渐增大,中心路段的运输承载量也逐步回升,当Q=450时,大多数中心路段的承载量已经回到了没有限制的水平.这正是图5中当Q=600时,总运输距离z和承载路段的数量回到无承载量限制水平的原因. 虽然分时段限流计划可以有效减少高峰路段的污染排放量.但限制中心路段流量,势必使得通过该中心路段的OD运输路径“改道”,造成总运输距离的增加,这也是物流活动中普遍存在的二律悖反规律. 图4 不同限载条件下承载量波动情况 图5 不同限载情况下总运输距离和道路 Fig.5Totaldistanceandamountofroadschanges underdifferentQ 分时段限流计划将主要的OD流运输安排在晚上,不但可以满足白天出行需求的高优先级,还可以满足需求点在白天时段的紧急需求,有效缓解各路段在白天时段内的交通状况;同时限定路段整体OD流的运输量,将尾气污染控制在环境自我调节量度之内,保证尾气污染所需要的扩散时间. 为了降低由密集运输流带来的道路环境污染问题,把一天划分为2个时段(7~22时和23~次日6时),限定路段在这2个时段不同的承载量,并将分布式OD运载网络和最短路径模型运用到多起终点运输问题中,建立分时段限流计划的整数规划模型,目标使总运输距离最小化.计算结果是一种不可公度解,且存在二律悖反规律.因此,所用分析方法为决策者根据不同目标作出不同计划提供依据.下一步的研究可从以下几方面入手:1)由于路段的拥挤,司机有可能会临时 “绕道”行驶,那么由O和D确定的路径在最短路及基础上具有一定随机性,即该需求确定的途径道路可能并不完全确定;2)在分时段限流优化中考虑OD流的K-最短路可以更有效地处理各路段承载量均衡和总运输量之间的关系.这两个方面的研究可同时加入车辆尾气排放量与车辆载荷、能耗、车速和车型等的关系;可根据居民区和道路建造情况,设置不同的路段承载力进行研究. [1] 卫振林, 申金升, 徐一飞.交通环境容量与交通环境承载力的探讨[J]. 经济地理, 1997, 17(1): 97-99. [2] Ubeda S, Arcelus F J, Faulin J. Green logistics at Eroski: A case study[J].InternationalJournalofProductionEconomics, 2011, 131(1): 41-51. [3] Caniato F, Caridi M, Crippa L, et al.A framework for measuring logistics performance in the wine industry[J].InternationalJournalofProductionEconomics, 2012, 135(2): 659-670. [4] Hu T L, Sheu J B, Huang K H. A reverse logistics cost minimization model for the treatment of hazardous wastes[J].TransportationResearchPartE:LogisticsandTransportationReview, 2002, 38(6): 457-473. [5] Murphy P R, Poist R F, Braunschweig C D. Information: title: role and relevance of logistics to corporate environmentalism: an empirical assessment [J].InternationalJournalofPhysicalDistributionandLogisticsManagement, 1995, 25(2): 5-19. [6] Harris I, Naim M, Palmer A, et al. Assessing the impact of cost optimization based on infrastructure modeling on CO2emissions[J].InternationalJournalofProductionEconomics, 2011, 131(1): 313-321. [7] Wahab M I M, Mamun S M H, Ongkunaruk P. EOQ models for a coordinated two-level international supply chain considering imperfect items and environmental impact[J].InternationalJournalofProductionEconomics, 2011, 134(1): 151-158. [8] 肖丁丁,张文峰.基于DEMATEL方法的绿色物流发展关键因素分析[J]. 工业工程, 2010, 13(1): 52-57. Xiao Dingding, Zhang Wenfeng.Key element analysis for green logistics development by using decision making trial and evaluation laboratory method[J].IndustrialEngineeringJournal, 2010, 13(1): 52-57. (in Chinese) [9] 马玉立.我国绿色物流的发展障碍及对策研究[J]. 中国商贸, 2012(3): 167-168. [10] Guo R Y, Huang H J. Network traffic flow evolution model consideringODdemand mutation[J].SystemsEngineering-Theory&Practice, 2009, 29(1): 118-123. [11] Mínguez R , Sánchez-Cambronero S , Castillo E , et al.Optimal traffic plate scanning location for OD trip matrix and route estimation in road networks[J].TransportationResearchPartB:Methodological, 2010, 44(2): 282-298. [12] Nie Y M, Zhang H M. A variational inequality formulation for inferring dynamic origin-destination travel demands[J].TransportationResearchPartB:Methodological, 2008, 42(7/8): 635-662. [13] 程紫润, 傅大放, 魏家泰.汽车尾气的初期扩散与扩散参数[J]. 中国环境科学, 1994, 14(1): 17-21. Cheng Zirun, Fu Dafang,Wei Jiatai.The initial dispersion and dispersion parameters of vehicle pollutants[J].ChinaEnvironmetalScience, 1994, 14(1): 17-21. (in Chinese)2 模型
2.1 多OD流最短路径模型



2.2 多OD流分时段限流模型
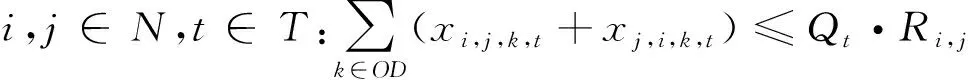
3 实验仿真
3.1 参数设置和决策变量的降维操作

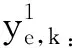
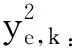

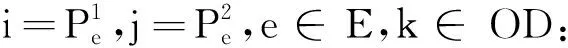
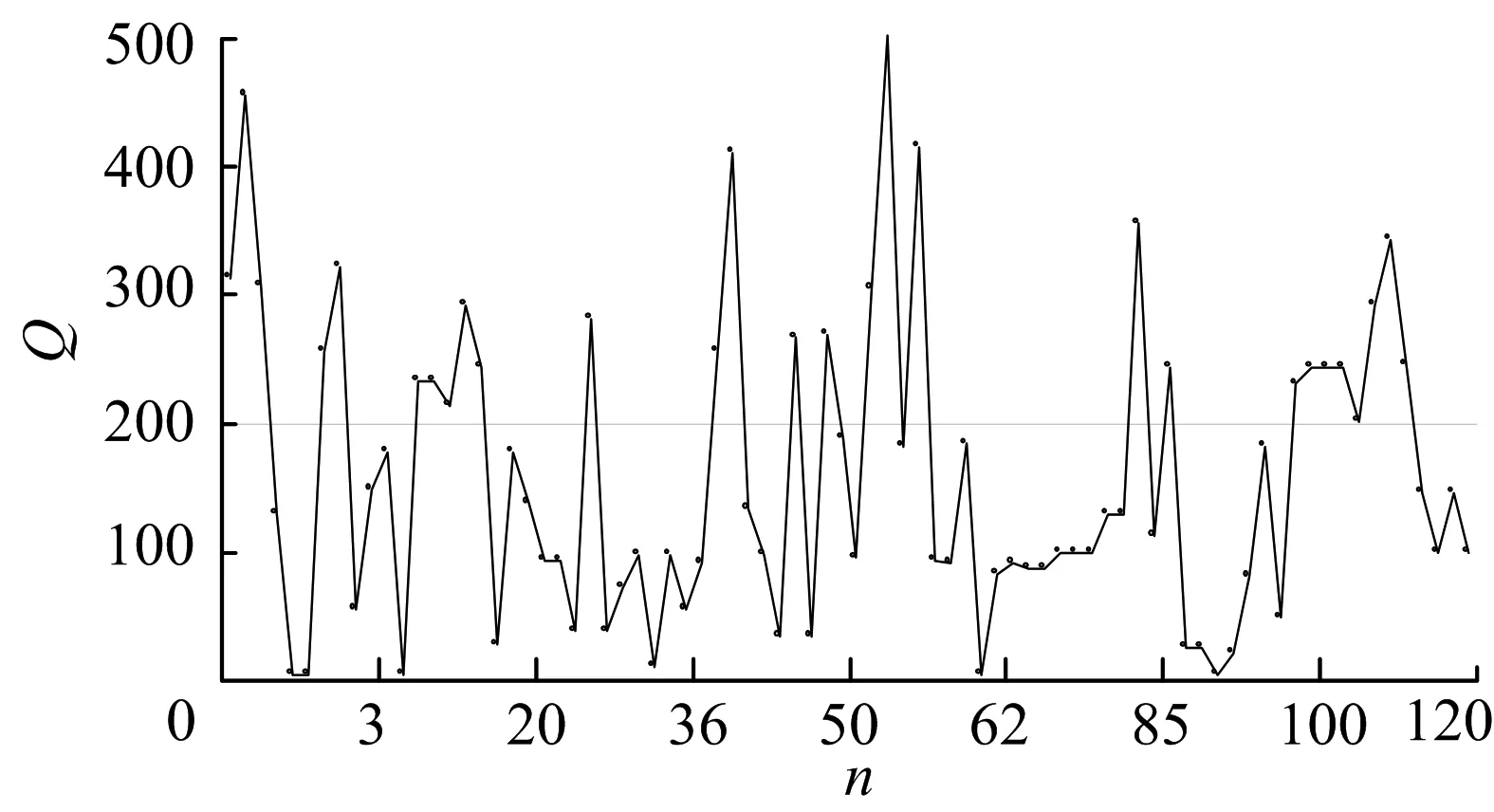
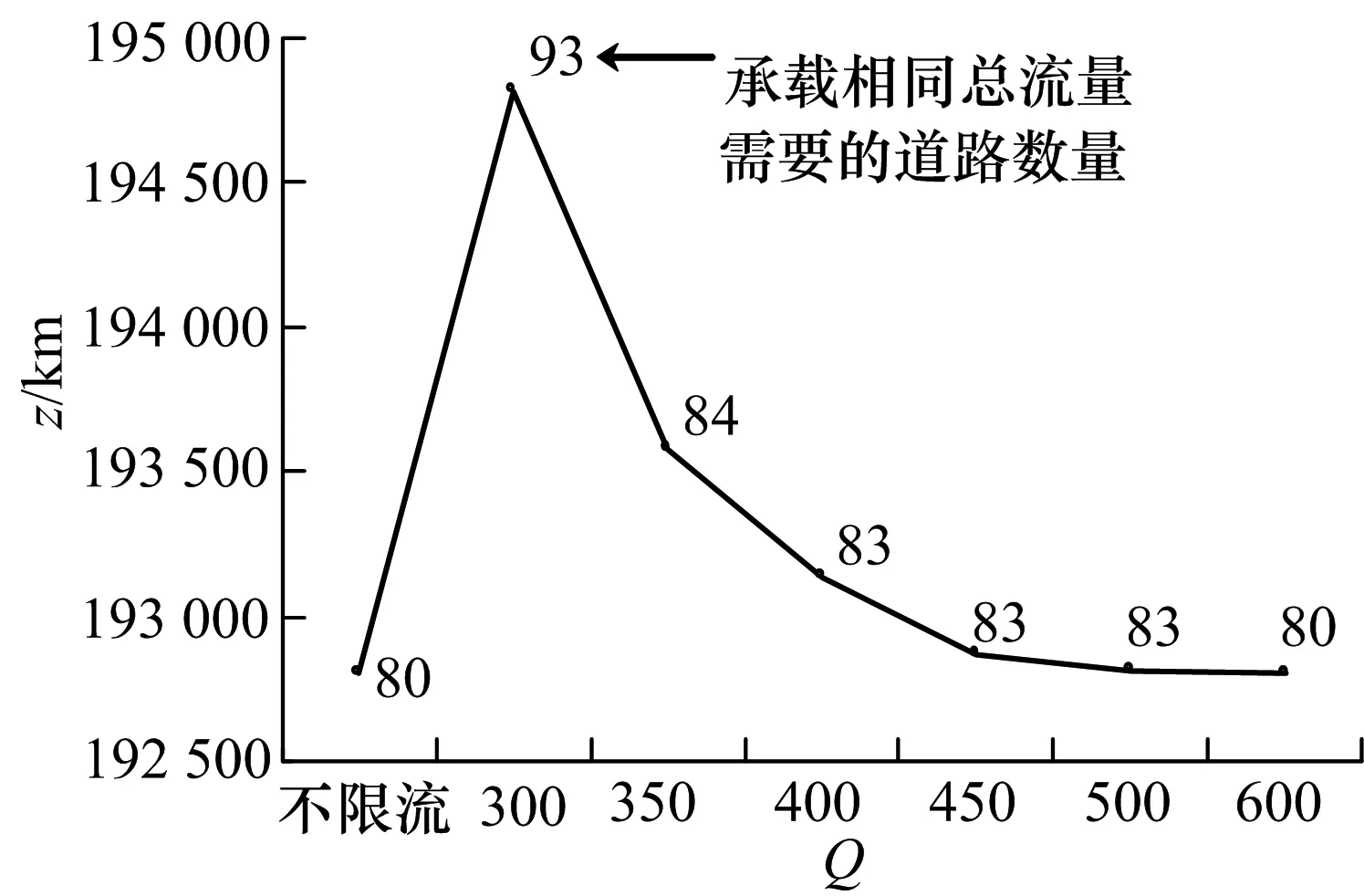
3.2 实验结果分析


4 结论

