N型四能级原子介质中古斯-汉欣位移的相干控制

邓文武

(1.华中师范大学物理科学与技术学院，湖北 武汉 430079； 2.咸宁学院光子学与光子技术研究所，湖北 咸宁 437100)

当光束在两种介质分界面上发生全反射时，反射光相对于入射光在空间上有一侧向位移，这一侧向位移被称为古斯-汉欣(GH)位移. 它是由Goos和Hänchen[1-2]两位物理学家在实验上首先发现. 之后，人们采用了相位法[3]、能量守恒[4]等不同的理论成功地解释了这种现象. 由于古斯-汉欣位移在薄膜光学[5]、光波导开关[6]、光学传感器[7]和波导[8]等方面有着非常重要的、潜在的应用，一直是研究热点. 例如在波导中，由于古斯-汉欣位移的影响，光波导的有效宽度发生变化，改变了电磁波在波导中的振幅，从而使电磁波的传播能量发生变化. Li[8]等人发现在负的折射系数波导中，由于古斯-汉欣位移引起的传播能量变化，使原子介质的自发辐射增强了好几个数量级，这种效应在强相互作用或量子点中有着潜在的应用[8,9]，受到人们越来越多的关注.

古斯-汉欣位移的数值只有波长数量级，很难观察到，其测量有一定的困难.因此，近些年来，人们采用各种方法来有效地调控和增强古斯-汉欣位移. 早期，主要集中在选用不同种类、不同结构的介质来实现负、正向位移的增强，例如：弱吸收介质[10，11]、光子晶体[12-14]、负折射材料[15]等. 然而，这些研究都是通过改变介质的结构或种类来实现的. 对于具有固定结构或固定种类的体系，古斯-汉欣位移不易于操控.

光在介质中的传播可以用传播矩阵有效地描述，传播矩阵元与介质的吸收-色散性质有关.2002年，Scully[16]发现利用外加激光驱动场可以有效地调控介质的吸收-色散性质. 基于此方案的思路，各种不同的、利用外加强驱动场来改变介质吸收-色散性质从而达到调控、增强古斯-汉欣位移的方案被提出，从而使古斯-汉欣位移的研究进一步热起来. 这些方案与以前的方案显著的不同点在于通过外加驱动场直接调控古斯-汉欣位移，在实际应用中具有更好的操作性. 例如，Wang[17]等人考察了腔中二能级原子，通过改变外加控制场的强度和场与原子的失谐量，成功实现了很大的负向和正向位移.随后Ziauddin[18]等人又分析了腔中三能级和四能级原子的古斯-汉欣位移，发现对于超快光三能级电磁感应透明(EIT)结构中存在强的吸收，对出现大的位移不利，而采用四能级原子克服了这一不利因素.

光在介质中传播被介质吸收，在实际的古斯-汉欣位移应用中，人们关注的是尽可能在弱吸收情况下利用古斯-汉欣位移. 电磁诱导透明介质是实现这种弱吸收的理想介质. 最近的研究表明，电磁诱导透明区域附近对古斯-汉欣位移的控制比强吸收或强放大特性下要灵敏，即电磁诱导透明区域是实现古斯-汉欣位移突变和增强的最佳区域[19].本文中基于这一特性，讨论了腔中如图1(b)所示N型四能级介质在外加控制场的作用下对古斯-汉欣位移的影响. 如果不考虑能级|4〉，原子便简化为典型的Λ型电磁诱导透明结构介质. 让Λ型的三能级|1〉、|2〉、|3〉工作在电磁诱导透明区域的弱吸收附近，使介质处在能够实现古斯-汉欣位移突变和增强的最佳区域，然后通过能级|4〉所加的弱信号场更加有效地调控古斯-汉欣位移. 研究表明，通过对外加弱信号场的强度和失谐的调控，在介质对探测光的吸收较弱的情况下，能够有效的调控和实现大的、负向古斯-汉欣位移.

1 理论模型

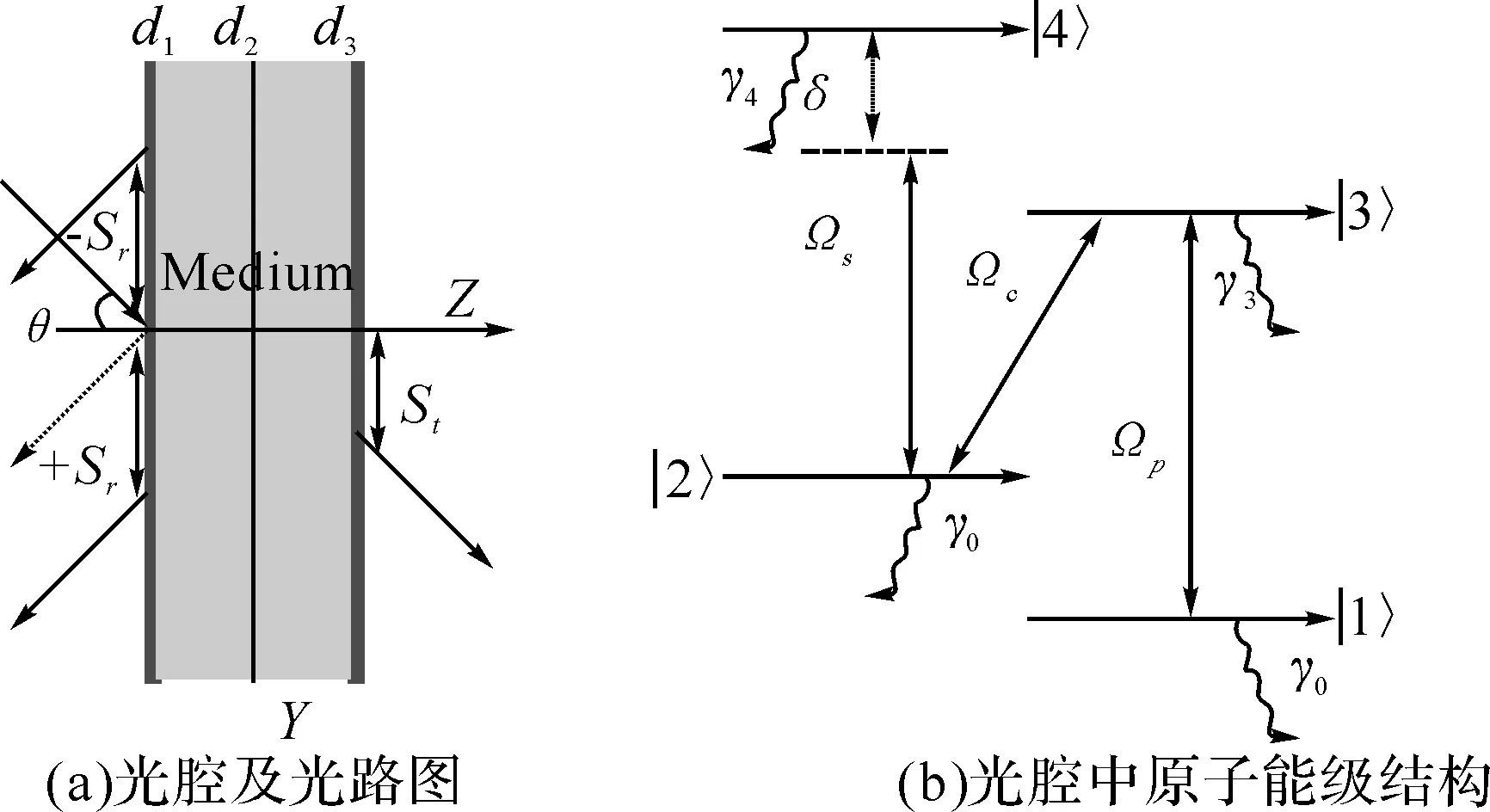
图1 理论模型

如图1(a)所示，频率为ωp的弱探测场从真空以θ角入射到腔中，腔由厚度分别为d1、d3非电磁透明极板组成，介电常数为ε1，弱入射探测光Ωp以θ角入射到透明腔板，θ角表示入射光线与Z轴的夹角. 弱入射探测光经过第一层透明腔板、腔内原子介质和第三层透明腔板后透射出来，对应透射光的侧向位移为St，对应反射光的侧向位移为Sr. 原子介质被Y轴方向加入的强驱动场Ωc和弱信号驱动场Ωs驱动.腔内的N型四能级原子介质厚度为d2.原子结构如图1(b)所示， 弱探测场、弱信号场、强控制场分别对应|1〉↔|3〉、|2〉↔|4〉、|2〉↔|3〉跃迁，原子的拉比频率分别为Ωp、Ωs、Ωc；弱信号场的频率与|2〉↔|4〉跃迁频率的失谐量为δ；原子各能级|4〉、|3〉、|2〉、|1〉的衰减系数分别为γ4、γ3、γ0、γ0，其满足γ4、γ3≫γ0.假定体系在任意时刻的态函数为|Ψ(t)〉=c4(t)|4〉+c3(t)|3〉+c2(t)|2〉+c1(t)|1〉，在偶极和旋波近似下，运用 Weisskopf-Wigner理论及旋转变换坐标系中的薛定谔方程，容易得到原子各个能态几率幅随时间的演化方程满足(ħ=1)：

(1a)

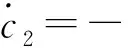
(1b)

，

(1c)

(1d)

其中：Γ4=iδ+γ4/2、Γ3=γ3/2、Γ0=γ0/2.

(1)式中已唯象地引入了原子的衰变效应.考虑弱探测场近似Ωp≫γ3及弱信号场与原子跃迁的大失谐，可知原子几乎始终在基态|1〉上，即：|c1|2≈1，容易得到(1)式在稳态情况下的解. 在探测场作用下原子介质的极化率χ=χ′+iχ″满足[20]：

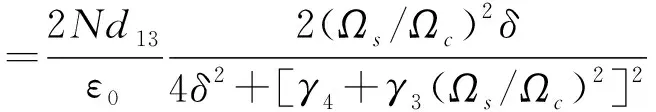
(2a)

(2b)

其中N、d13分别代表原子的密度和偶极跃迁矩阵元.χ′对应原子介质的色散性质，χ″反映原子介质的吸收特性.

2 古斯-汉欣位移及其数值分析

根据光在介质中的特征传播矩阵，探测场在第j层介质中的传播矩阵为[21]

(3)

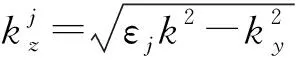
(4)

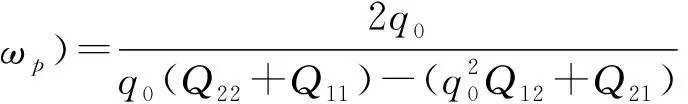
(5)

其中，q0=kz/k，Qij为总的传播矩阵Q的矩阵元.令R(ky，ωp)= |R(ky，ωp)|exp[iφr(ky，ωp)]，T(ky，ωp)=|T(ky，ωp)|exp[iφt(ky，ωp)],其中，φr、φt分别为反射系数和透射系数的相位.则有：

(6a)

(6b)

(7)

(8)

(9)

下面分析在不同的条件下，弱信号场Ωs对探测场的古斯-汉欣位移的影响. 从(8)式及(9)式中可以看出古斯-汉欣位移与介质厚度d2、极板厚度d1(d3)、极板介电常数等密切相关. 为了讨论方便，假定d1=d3=0.2 μm、d2=5 μm、ε1=ε3=2.22，探测场的频率ωp=2π×300 THz，同时令β=Nd13/ε0=2γ、γ=γ3=γ4、γ0=0.1γ、γ=1 kHz.

图2给出了当控制场Ωc=5γ、探测场Ωp=0.2γ、失谐量δ=0时，弱探测场的反射光(实线)和透射光(虚线)的古斯-汉欣位移Sr，t/λ随入射角θ的变化规律.当信号控制场不存在(Ωs=0)时，如图2(a)所示的N型四能级原子结构退化为典型的Λ型三能级原子结构.当强控制场Ωc≫Ωp，且γ3≫γ0时，此等效的三能级原子便是EIT结构，同时当强控制场Ωc与原子能级跃迁|2〉↔|3〉共振时，原子便出现电磁感应透明现象，此时原子介质对探测场的吸收为零，对应(2b)式χ″=0. 从图2(a)可知原子介质对探测场的吸收为零(透明点)时，反射光和透射光的古斯-汉欣位移完全重合，这一结果与文献[18]中三能级EIT介质中透明点处探测光的古斯-汉欣位移的变化规律完全一致. 当入射角θ的取值较大时，反射光和透射光的古斯-汉欣位移便可达到约280倍波长的正向位移.

(a)Ωs=0

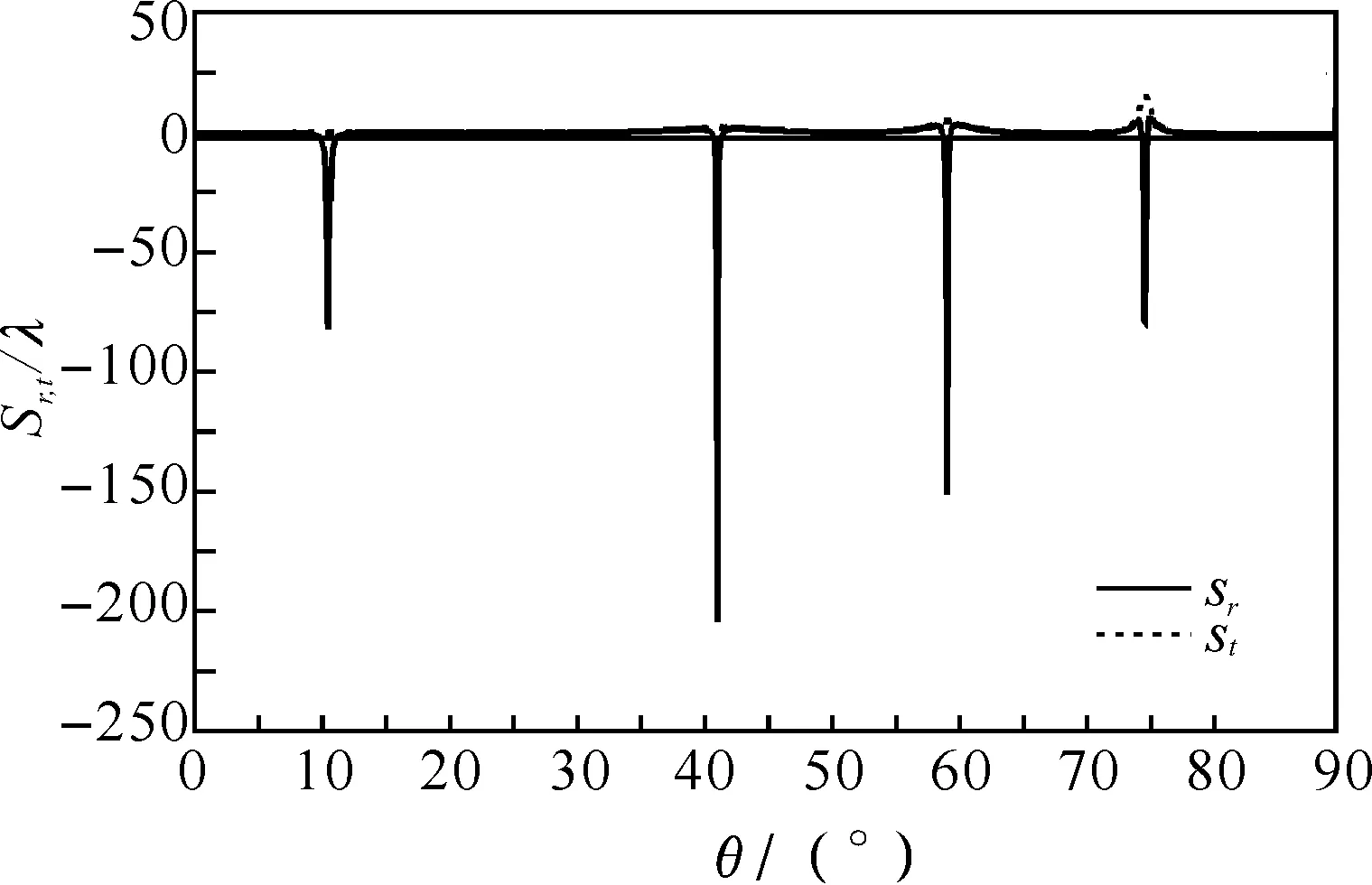
(b)Ωs=0.1γ

但是，在实际应用中，人们关注的是如何在介质对探测场极弱吸收情况下，实现大的、能够改变位移正负的古斯-汉欣位移调控. 从(2b)式中可以看出当Ωc≫Ωs时介质对探测场的吸收较弱. 下面分别考察介质对探测场极弱吸收情况下，弱信号场强度Ωs及其原子失谐量δ对古斯-汉欣位移的影响.

图2(b)给出了在弱信号场Ωs=0.1γ、其他条件与Ωs=0时相同的情况下，反射光(实线)和透射光(虚线)的古斯-汉欣位移Sr，t/λ随入射角θ的变化规律. 图中反射光和透射光的古斯-汉欣位移在峰值处不再重合，可以通过外加弱信号控制场来实现对古斯-汉欣位移的调控. 当介质处在弱吸收状态时，反射光的古斯-汉欣位移由透明点的正值转变为在某些角度处幅度很大的负值，可以通过对信号场的微调使反射光的古斯-汉欣位移出现负的侧向位移. 而透射光的古斯-汉欣位移仍为正值，且在某些角度处要小于透明点时的位移.

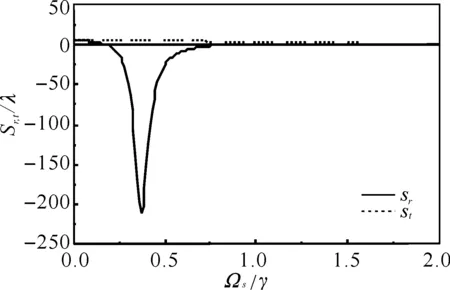
图3 反射光的古斯-汉欣位移Sr/λ(实线)和透射光的古斯-汉欣位移St/λ(虚线)随弱信号场强度ΩS的变化规律

图4 反射光的古斯-汉欣位移Sr/λ(实线)和透射光的古斯-汉欣位移St/λ(虚线)随失谐量δ的变化规律

图3给出了在固定入射角θ=60°、Ωc=5γ、Ωp=0.2γ、δ=2γ时，反射光(实线)和透射光(虚线)的古斯-汉欣位移Sr,t/λ随信号控制场Ωs的变化规律. 从图中可以看出在信号控制场较弱的情况下(对应介质的弱吸收)，反射光的古斯-汉欣位移对信号控制场强度的变化比较灵敏，可以实现大的负古斯-汉欣位移；而透射光的古斯-汉欣位移对信号控制场强度的变化表现得比较迟缓，仍然为正值. 随着信号控制场强度的增强，介质表现出强吸收，反射光(实线)和透射光(虚线)的古斯-汉欣位移表现得越来越迟缓，并且位移的幅度也变小了. 因此，调节信号控制场，可以使介质处在对探测光弱吸收的情况下对反射光的古斯-汉欣位移进行有效的调控.

进一步分析外加弱信号场对古斯-汉欣位移的调控，图4给出了在弱吸收(Ωs=0.1γ)的情况下，当固定入射角θ=60°、Ωc=5γ、Ωp=0.2γ时，弱信号场与原子的失谐量δ对反射光(实线)和透射光(虚线)的古斯-汉欣位移Sr,t/λ的影响.从图中可以看出在失谐量较小的范围内，失谐对反射光的古斯-汉欣位移影响较大，可以使古斯-汉欣位从正的到负的位移，而对透射光的古斯-汉欣位移基本没有影响.

3 结论

光腔中的介质在电磁感应透明的状态下通过外加弱信号控制场的调控，使腔中四能级原子介质在弱吸收情况下调控探测光的古斯-汉欣位移. 与选用不同种类的电介质或不同结构的电介质调控古斯-汉欣位移相比，此方法不需要改变体系的物理结构，通过外加驱动场的调控，更易于调控古斯-汉欣位移. 分析得出：在没有外加弱信号控制场的电磁感应透明状态，反射光和透射光的古斯-汉欣位移完全重合；当加上弱信号控制场，反射光的古斯-汉欣位移对弱信号场强度、失谐量的变化比较灵敏，可以调控、改变古斯-汉欣位移正负方向，实现大的、负向古斯-汉欣位移.

[1] Goos F，Hänchen H. Ein neuer and fundamentaler versuch zur totalreflexion[J].Ann Phys， 1947， 1(6):333-336.

[2] Goos F，Hänchen H. Neumessang des strahlversetzungeffkets bei totalreflexion[J].Ann Phys， 1949， 5(3):251-253.

[3] Artmann K. Berechnung der seitenversetzung des totalreäektierten strahles[J].Ann Phys， 1948， 437:87-97.

[4] Steinberg A M，Chiao R Y. Tunneling delay times in one and two dimensions[J].Phys Rev A， 1994， 49:3283-3287.

[5] Harrick N J. Study of physics and chemistry of surfaces from frustrated total internal reflections[J].Phys Rev Lett， 1960(4):224-227.

[6] Sakata T，Shimokawa T H. Reflection-type 2×2 optical waveguide switch using the Goos-Hänchen shift effect[J] Appl Phys Lett， 2000， 76:2841-2844.

[7] Yin X B，Hesselink L. Goos-Hänchen shift surface plasmon resonance sensor[J].Appl Phys Lett， 2006， 89:261108-261112.

[8] Li G X， Evers J，Keitel C H. Spontaneous emission interference in negative-refractive-index waveguides[J].Phys Rev B， 2009， 80:045102-045108.

[9] Yao P J， Vlack C V， Reza A， et al. Ultrahigh purcell factors and lamb shifts in slow-light metamaterial waveguides[J].Phys Rev B， 2009， 80:195106-195116.

[10] Lai H M，Chan S W. Large and negative Goos-Hänchen shift near the Brewster dip on refraction from weakly absorbing media[J].Opt Lett， 2002， 27:680-684.

[11] Wang L G， Chen H，Zhu S Y. Large negative Goos-Hänchen shift from a weakly absorbing dielectric slab[J].Opt Lett， 2005， 30:2936-2941.

[12] Felbacq D， Moreau A，Smaali R. Goos-Hänchen effect in the gaps of photonic crystals[J].Opt Lett， 2003， 28:1633-1638.

[13] Smaali F D. Bloch modes dressed by evanescent waves and the generalized goos-Hänchen effect in photonic crystals[J].Phys Rev Lett， 2004， 92:193902-193906.

[14] Wang L G and Zhu S Y. Giant lateral shift of a ligh tbeam at the defect mode in one-dimensional photonic crystals[J].Opt Lett， 2006， 31:101-104.

[15] Berman P R. Goos-Hänchen shift in negatively refractive media[J].Phys Rev E， 2002， 66:067603-067607.

[16] Scully M O. Enhancement of the index of refraction via quantum coherence[J].Phys Rev Lett， 2002， 67:1855-1858.

[17] Wang L G， Ikram M，Zubairy M S. Control of the Goos-Hänchen shift of a light beam via a coherent driving field[J].Phys Rev A， 2008， 77:023811-023816.

[18] Ziauddin， Qamar S， Zubairy M S. Coherent control of the Goos-Hänchen shift[J].Phys Rev A， 2007， 81:023821-023825.

[19] 邓文武. 基于外加驱动场的相干调控来增强古斯-汉欣位移[J].重庆理工大学学报：自然科学， 2011， 25(11)：115-119.

[20] Carvalho S A，Araujo L E E. Electromagnetically induce blazed grating at low light levels[J].Phys Rev A，2011， 83:0053825-0053830.

[21] 赵建林. 高等光学[M].北京:国防工业出版社，2003.

[22] Born M，Wolf E. Principles of optics[M].Cambridge:Cambridge University Press， 1999.