聚合物驱产油量预测模型的比较研究

丁显峰

(西南石油大学理学院，四川 成都 610500)

邱海燕

(西南石油大学化学化工学院，四川 成都 610500)

聚合物驱产油量预测模型的比较研究

丁显峰

(西南石油大学理学院，四川 成都 610500)

邱海燕

(西南石油大学化学化工学院，四川 成都 610500)

聚合物驱产油量预测结果的可靠性直接关系到油田开发年度规划和中长期规划的编制部署，因此预测模型的选择尤为重要。介绍了聚合物驱产油量预测的5种模型：广义翁氏模型、Weibull模型、瑞利模型、Logistic模型和HCZ模型。应用这5种模型分别对克拉玛依油田七东区三采克下组聚驱产油量进行了预测，对比分析表明Weibull模型和Logistic模型对实际产油量拟合程度较其他3种模型高，预测结果误差均在10%以内；各个模型考虑的因素不尽相同，在进行实际应用前应对这些模型择优利用。

聚合物驱；产油量；预测模型

聚合物驱是油田继水驱后广泛采用的提高采收率技术。目前，研究常规聚合物驱产油量预测方法很多[1-4]，不同的预测方法从不同的角度对各方面有用的信息进行挖掘整理，所利用的信息也是不相同的；同时，由于预测环境中不同影响因素的相互作用，真实过程可能会以人们预想不到的方式进行变化，针对某些因素所建立的预测模型就会面临假设性错误的风险，因此，选择合适的预测模型对聚驱产量的预测尤为重要。笔者通过分析5种预测模型的特点，比较了5种模型在聚合物驱中的预测效果，为选择合适的预测模型提供依据。

1 预测模型

聚合物驱的有效期比水驱短，一般为2～5年，因此为保证预测模型取得较好的预测效果，将聚合物驱产油量预测的单位时间取为月。

1.1广义翁氏模型

广义翁氏模型[5]是1996年陈元千和胡建国在翁氏模型的基础上，基于概率统计学中的伽马分布进一步推导而得到的。该模型被广泛应用在油气田产量的预测之中，效果较好。具体表达式为:

Q=atbe-(t/c)

(1)

式中，a、b、c为3个模型参数；t=y-y0，t为生产时间，mon；y为预测的月份；y0为预测产量的起始月份；Q为某一生产时间的产量，t。

1.2Weibull模型

Weibull模型[6-7]即Weibull 1939年提出的统计分布模型，该模型的分布密度函数在随机变量[0,+∞)区间内的积分为1，聚合物驱产油量与累积产油量的比值随聚合物驱生产时间的变化具有相似特征，因此，聚合物驱的产油量可表示为：

(2)

式中，α、β为模型参数；NR为聚合物驱阶段油田的可采储量，t。

1.3瑞利模型

瑞利模型[8]也是基于数理统计中瑞利分布密度函数，在随机变量[0,+∞)区间内的积分为1，与Weibull模型类似，聚合物驱的产油量可表示为：

(3)

令a=2NR/c，则有：

Q=ate-(t2/b)(a、b为模型参数)

(4)

1.4Logistic模型

Logistic模型[9-10]是一个属于增长类型的模型，由美国Hubbert于1962年首次提出，又称Hubbert模型。其表达形式为：

(5)

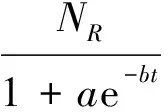
(6)

1.5HCZ模型

HCZ模型[11]是1995年由胡建国、陈元千和张盛宗基于累积产量随时间递增的信息特征，结合大量油气田的统计研究成果，推导建立的预测模型。该模型可用于预测油气田的产量、累积产量、可采储量和最高年产量及其发生的时间,并能简化为广泛应用于经济增长预测和资源增长预测的龚帕兹(Gompertz)预测模型。其具体表达式为：

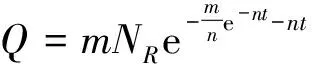
(7)

2 实例分析

克拉玛依油田七东区三采克下组2006年9月开始注聚合物，聚合物驱含油面积1.25km2，有效厚度14.8m，地质储量193.9×104t，总井数9口，采用200m井距五点法面积井网进行开采。利用七东区三采克下组的生产数据，对式(1)、(2)、(4)、(6)和(7)进行线性回归分析，结果如下：

广义翁氏模型：a=26.40，b=2，c=13.97，相关系数R=-0.9973。

Weibull模型：α=2.3，β=3760.95，NR=109656.2，相关系数R=-0.9944。

瑞利模型：a=155.7168，c=1705，相关系数R=-0.9750。

Logistic模型：a=708.74，b=0.02625，NR=121765.4，相关系数R=-0.9967。

HCZ预测模型：m=0.2150，n=0.0514，NR=135716.7，相关系数R=-0.9911。

图1 实际产油量与预测产油量对比

各模型预测产油量与实际产油量见图1。从图1中可以看出，在产量初始上升阶段各预测模型预测数值，广义翁氏模型和Weibull模型预测误差较大，其他3种模型误差较小，基本没有太大差异；在产量快速上升阶段HCZ模型误差最大，瑞利模型误差次之，Weibull模型和Logistic模型预测数值的误差最小；达到聚驱最大产量后，Weibull模型和Logistic模型预测值下降趋势较其他3种模型大，瑞利模型和广义翁氏模型下降趋势较小，HCZ模型从整体上看只适合作为聚合物驱产油量初始上升和下降阶段的预测；从整个预测数据与实际数据对比看，Weibull模型和Logistic模型预测比较准确，拟合程度较高。

表1为最后10个月的实际产量和各模型预测值误差对比，通过实际值与预测值的比较可见， 除HCZ模型初始预测相对误差较大外，误差均在10%以内；比较而言Weibull模型和Logistic模型在整个聚合物驱生产过程中拟合程度高，预测结果误差小，适合聚合物驱产量的预测。

表1 实际产量和各模型预测值误差对比

3 结 论

1)在整个聚驱产量预测过程中Weibull模型和Logistic模型更符合聚合物驱的实际生产动态，对油田聚驱产油量的预测结果更符合实际情况，误差都低于10%；瑞利模型和广义翁氏模型预测的结果精确程度稍差些；由于HCZ模型预测误差较大，建议在克拉玛依油田不使用该模型预测。

2)关于聚合物驱产油量预测模型很多，对于相同的实例，不同的预测模型结果是有差异的，各个模型考虑的因素也不尽相同。聚合物驱油的机理较为复杂，要建立准确的和普适的预测模型较为困难，只能说某一模型更适合于某一特定条件的油田，所以对于这些模型择优利用，才能达到最优化设计的目的。

[1]刘朝霞,张禹坤,蒋平.Weibull与HCZ预测模型在聚合物驱产油量预测中的应用[J].油气地质与采收率,2007,14(6):76-78.

[2]孙强,邓兵,马丽梅.广义翁氏与瑞利模型在聚合物驱产量预测中的应用[J].大庆石油地质与开发,2003,22(5):58-59.

[3]黄学,刘朝霞,韩冬，等.一种预测聚合物驱开发动态的新模型[J].石油勘探与开发,2009,36(2):228-231.

[4]石成方,肖伟,王凤兰.聚合物驱油开发指标预测模型[J].石油学报,2005,26(5):78-80,84.

[5]陈元千,胡建国.对翁氏模型建立的回顾及新的推导[J].中国海上油气地质，1996,10(5):317-324.

[6]陈元千.预测油气田产量的Weibull模型[J].新疆石油地质,1995,16(3): 250-255.

[7]陈元千,赵庆飞.Weibull预测模型与乙型水驱曲线的联解法[J].新疆石油地质,2000,21(5): 405-407.

[8]陈元千.瑞利模型的完善推导与应用[J].油气地质与采收率,2004,11(4):39-41.

[9]陈元千，胡建国，张栋杰.Logistic模型的推导及自回归方法[J].新疆石油地质,1996,17(2): 150-155.

[10]乐平，陈小凡，崔力公，等.产量研究中翁氏模型和Logistic模型的建议求解[J].石油天然气学报(石油天然气学报)，2009,31(4): 277-279.

[11]胡建国,陈元千,张盛宗.预测油气田产量的新模型[J].石油学报,1995,16(1):79-86.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.12.024

TE357

A

1673-1409(2012)12-N074-03