基于相对斜率的改进灰色关联度模型研究

马引弟

(陕西理工学院数学与计算机科学学院，陕西 汉中 723000)

基于相对斜率的改进灰色关联度模型研究

马引弟

(陕西理工学院数学与计算机科学学院，陕西 汉中 723000)

通过对现有灰色关联度模型的研究，依据数据序列时点间相对斜率差来计算关联系数，以灰色关联系数均值的修正值作为序列的关联度，提出了改进的灰色关联度模型，并研究了改进模型的性质。研究表明，利用该方法所得分析结果与定性分析相一致，且分辨效果更好，因而具有可行性。

灰色关联度；相对斜率；稳定度

灰色关联分析是灰色系统理论的重要组成部分，其主要通过系统数据序列曲线的几何形状的相似和相近程度，用量化的方法判断序列间关联程度的大小，曲线越接近，形状越相似，相应序列间的关联度越大，反之越小。目前有关关联度的量化模型很多[1-6]，这些模型从不同角度考虑了曲线相似性的衡量问题，在社会经济和生产实践中取得了一定的应用效果，但也存在各种缺陷，如容易受到数据极值和采样数据质量的影响、不满足整体性公理、不能反映序列间的正负相关性、不满足规范性和保序性、没有考虑到稳定性等。为此，笔者从分析事物发展规律的角度出发，提出了一种改进的灰色关联度模型。该模型以系统数据序列中相邻时点间的相对斜率差作为计算灰色关联系数的依据，引入符号函数来反映序列的正负相关关系，利用点关联系数序列稳定度[7]的概念来计算关联度，并讨论了改进模型的性质，最后通过实例验正了该方法的实用性。

1 改进的灰色关联度模型及性质

1.1改进灰色关联度模型的建立

建立改进灰色关联度模型的基本思路如下：采用序列中相邻时点间的相对斜率差的两极最大和最小差，综合考虑系统中比较序列对关联系数的影响，用灰色关联系数来衡量序列的局部相似性，以其均值表示2序列的整体相似度，最后利用点关联系数序列的稳定度对整体相似度进行修正，从而得到改进的灰色关联度。

具体计算方法如下：

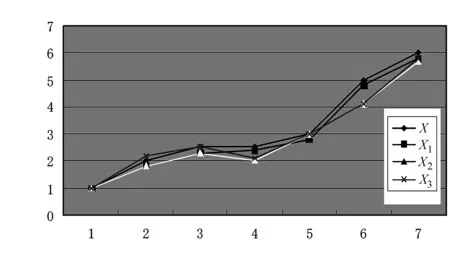
设时间区间[a,b]，0≤a

定义1设区间[a,b]上的系统特征序列为X={x(t1),x(t2),…x(tn)}，系统行为序列为Xi={xi(t1),xi(t2),…xi(tn)}(i=1,2,…m)，称:

(1)

为X与Xi在时点t到时点t+Δt的灰色关联系数，ρ∈[0,1]，其中：

注：当X与Xi(i=1,2,…m)均为1-时距离散序列时，X与Xi在时点t到时点t+Δt的灰色关联系数为：

(2)

(3)

称S(ξi)为序列X与Xi的点关联系数序列的稳定度。S(ξi)越大，点关联系数序列稳定性越差。

为序列X与Xi的改进灰色关联度。

1.2改进灰色关联度模型的性质

性质2具有整体性；

性质4具有保序性，即对原始序列进行无量纲化处理，不会改变灰色关联度的值。

因无量纲化处理对点灰色关联系数的计算没有影响，而灰色关联度的计算考虑的是点关联系数的整体稳定性，故不会改变灰色关联度的值。

2 算例分析

图1 数据序列的折线图

采用文献[4]的算例，设参考序列X=(1,2,2.5,2.5,3,5,6)，比较序列如下：

X1=(1,1.8,2.3,2.4,2.8,4.8,5.8)

X2=(1,1.8,2.3,2,3,4.1,5.7)

X3=(1,2.2,2.5,2.1,3,4.1,5.8)

数据序列的折线图如图1所示，计算结果如表1所示。

从图1可以看出，各比较序列相邻时点间斜率与参考序列相邻时点间斜率的接近情形：序列X1与参考序列最接近，序列X2,X3与参考序列的差异要大一些，且X2,X3与参考序列的近似程度相差不多。

表1 关联度的比较

结合图1的分析，从表1可以看出，邓氏灰色关联度与实际情况不符，而改进模型以时点间相对斜率差作为灰色关联系数的计算依据，考虑了序列各时点的正、负相关关系，并从整体上消除了点关联系数的显著差异对关联度的影响。序列X1与参考序列在各时点间的相对斜率差异小，序列X2、X3与参考序列的差异大，同时在某些时点间X2、X3与参考序列相交，改进模型考虑了序列间的这些差异，正确反映了比较序列与参考序列相近程度的次序，所得结果与定性分析相一致，和实际情况是相符的。

3 结 语

在邓氏灰色关联度和灰色斜率关联度的基础上，建立了一种基于时点间相对斜率差的改进灰色关联度模型。该模型从分析事物发展规律的角度，综合考虑了整体性对关联度的影响，能够反映序列各时点的正、负相关关系，且不受无量纲变换处理的影响，并有效地解决点关联系数具有显著差异下的关联度计算问题。算例分析表明，改进后的模型所得结果与定性分析相一致，分辨效果清晰。该模型在一定程度上改进了灰色关联度模型的性能，拓宽了灰色关联度的应用范围，具有良好的实用性。

[1]邓聚龙.灰色系统的基本方法[M].武汉：华中理工大学出版社，1987.

[2]梅振国.灰色绝对关联度及其计算方法[J].系统工程，1992，10(5)：43-44.

[3]魏丽，陈丽宇.关于一类新的广义灰色关联度[J].宁夏大学学报(自然科学版)，2007，28(1):22-24.

[4]王靖程，诸文智，张彦斌.基于面积的改进灰色关联度算法[J].系统工程与电子技术，2010，32(4)：777-779.

[5]党耀国，刘思峰，刘斌，等.灰色斜率关联度的改进[J].中国工程科学，2004，6(3)：41-44.

[6]单联宏.灰色斜率关联度的改进及应用[J].长江大学学报(自然科学版)，2010，7(3)：N441-443.

[7]崔杰.点关联系数有显著差异下灰色关联分析模型的改进[J].统计与决策，2008(24)：4-6.

[编辑] 李启栋

10.3969/j.issn.1673-1409(N).2012.11.09

O29；N941 5

A

16731409(2012)11N02503