一种求解二层多目标规划问题的改进模拟退火算法

张 涛 陈 忠，吕一兵

(长江大学信息与数学学院，湖北荆州434023 水资源与水电科学国家重点实验室(武汉大学)，湖北武汉430072) (长江大学信息与数学学院,湖北 荆州 434023)

一种求解二层多目标规划问题的改进模拟退火算法

张 涛 陈 忠，吕一兵

(长江大学信息与数学学院，湖北荆州434023 水资源与水电科学国家重点实验室(武汉大学)，湖北武汉430072) (长江大学信息与数学学院,湖北 荆州 434023)

基于求解多目标规划问题的模拟退火算法，将求解二层多目标规划问题转化为交互求解下层多目标规划问题和上层多目标规划问题，然后结合求解多目标规划的精英策略，提出了求解二层多目标规划的改进模拟退火算法。最后，通过数值试验验证了算法的可行性和有效性。

二层多目标规划；Pareto最优解；模拟退火算法

二层多目标规划是二层规划的子问题，其主要特征是上层和下层都具有多个目标函数。求解二层多目标规划的主要难点在于：上层问题的可行解一定是下层问题的最优解。这就要求只能将下层问题的精确最优解反馈给上层。值得庆幸的是，大量实践表明，下层问题的近似最优解通常可以作为最优响应反馈给上层，从而通过上层问题的求解得到整个问题的近似最优解，然后再通过预设的迭代次数，可以使整个问题的近似最优解任意精度的逼近精确解。基于这种观念，模拟退火算法[1]对于求解二层多目标规划问题就有巨大的潜力。下面，笔者基于求解多目标规划问题的改进模拟退火算法，将求解二层多目标问题转化为交互求解下层多目标规划问题和上层多目标规划问题，再结合求解多目标规划的精英策略[2]，提出了求解二层多目标规划的模拟退火算法。

1 二层多目标规划模型

假设x∈Rn1,y∈Rn2,F:Rn1×Rn2→Rm1,f:Rn1×Rn2→Rm2,G:Rn1×Rn2→Rp,g:Rn1×Rn2→Rq，则二层多目标规划可以写为：

(1)

式中，F(x,y)和f(x,y)分别为上层目标函数和下层目标函数；G(x,y)和g(x,y)分别表示上层约束条件和下层约束条件。

假设：

S={(x,y)|G(x,y)≥0,g(x,y)≥0}

X={x|∃y,G(x,y)≥0,g(x,y)≥0}S(x)={y|g(x,y)≥0}

定义1固定x∈X, 如果y是下层问题的一个Pareto最优解，则(x,y)为问题(1)的可行解。

定义2如果(x*,y*)是问题(1)的可行解, 并且不存在(x,y)∈IR, 使得F(x,y)F(x*,y*), 则(x*,y*)是问题(1)的一个Pareto最优解, 其中 符号“” 表示Pareto偏好。

2 算法设计

2.1算法1

步1 根据当前解Xk和扰动量εk产生备选解Yk=Xk+εk。

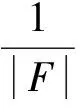
步3 计算转移概率p(Yk|Xk,Tk)=min{1,exp(ΔE(Xk,Yk))}。

步4 选择子代。若果p(Yk|Xk,Tk)≥η, 则Xk+1=Yk; 否则Xk+1=Xk。

2.2算法2

步1 对于第k(k=1,2,…,ns)个子群，在下层f空间给每个粒子分配非受控等级NDl以及拥挤度值CDl。然后将所有的子群合并成一个种群Pt，在F空间中对每个粒子分配非受控等级NDu以及拥挤度值NDu。

步2 将非受控等级NDu=1及NDl=1的粒子从Pt挑出，保存于精英集合At。

步3 对于第k个子群，更新下层决策变量。①设置下层循环变量tl=0；②对于固定的xj，利用算法1更新第j(j=1,2,…,Nl) 个粒子；③设置tl=tl+1；④如果tl≥Tl, 转 ⑤， 否则转②；⑤对于第i个子群中的每个粒子在f空间中重新分配非受控等级NDl和拥挤度值CDl。然后将所有的子群合并成一个种群，重新命名为Qt，并在F空间中对其重新分配非受控等级NDu和拥挤度值CDu。

步 4 将Pt和Qt合并为Rt，并在F空间中分配非受控等级NDu，具有相同等级的粒子计算其拥挤度值。

步 5 从Rt中选择一半粒子作为子代种群。 首先将NDu=1，NDl=1的粒子按照递减的拥挤度值CDu所对应的子群复制到中间种群St。然后考虑NDu=2的情况，依次类推直到St中包含ns个子群。

步6 根据精英策略更新精英集合At。

步7 在集合St中更新上层决策变量：①初始化上层循环次数tu=0；②对于固定的yi根据算法1更新第i个粒子 (i=1,2,…,Nu)；③ 设置tu=tu+1；④如果tu≥Tu, 转步⑤， 否则转②；⑤在F空间中，每个粒子分配非受控等级NDu和拥挤度值CDu。

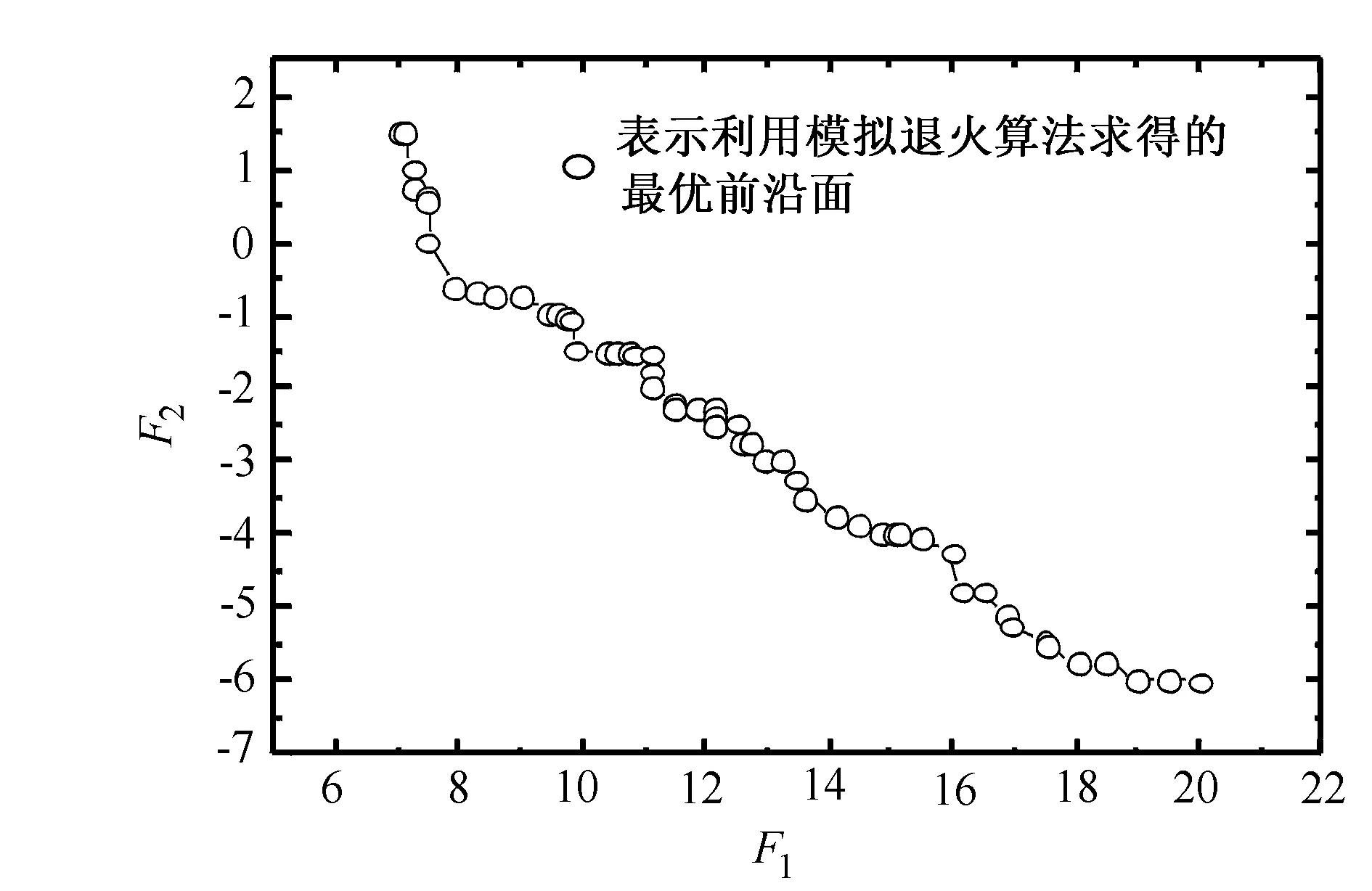
步 9 如果Tk

3 数值试验

根据算法2，利用c#进行编程(计算机配置：CPU:AMD 2.80GHz; RAM: 3.25GB)，所得数值结果如下。

参数设置如下:Nu=200，Tu=200,Nl=40,Tl=40,Tmax=106,Tf=10-3，m=3。根据算法2，利用c#进行编程(计算机配置：CPU: AMD 2.80GHz; RAM: 3.25GB)，所得数值结果如图1和图2所示。

图1 算例1的最优前沿面 图2 算例1的最优Pareto解集

算例2[4]:

图3 算例3的最优前沿面

参数设置如下:Nu=400，Tu=200,Nl=80,Tl=40,Tmax=107,Tf=10-3,m=3。根据算法2，利用c#进行编程(计算机配置：CPU: AMD 2.80GHz; RAM: 3.25GB)，所得数值结果如图3所示。

从算例1的结果可以很清楚的看到，利用改进的模拟退火算法所求得的问题的最优前沿面非常接近理论前沿面，并且可以均匀的分布于理论前沿面上；对于理论前沿面未知的算例2，利用改进的模拟退火算法所求的最优前沿面与文献[5]中所求解的最优前沿面非常的相似，从而说明该算法是可行并且是有效的。

[1]汪定伟，王俊伟，王洪峰，等. 智能优化算法[M]. 北京：高等教育出版社，2006.

[2] Deb K, Agrawalan S, Pratap A,et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002(6):182-197.

[3] Eichfelder G. Solving nonlinear multi-objective bi-level optimization problems with coupled upper level constraints[A]. Technical Report Preprint No. 320, Preprint-Series of the Institute of Applied Mathematics[C].Univ. Erlangen-Nrnberg, Germany, 2007.

[4] Eichfelder G.Multiobjective bilevel optimization[J]. Mathematical Programming, 2010, 123:419-449.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.11.001

O224

A

16731409(2012)11N00103