中国古代历法推算中的误差思想空缺

王玉民

(北京天文馆古观象台，北京 100005)

研究中国古代历法时，我们时常为古人计算动辄精确到小数点后6、7位，或使用巨大分子分母构成的精确数而惊叹，按说，用如此精密算法修成的历法，其可靠性也应该同样令人惊叹，然而，纵观各朝各代，一部历法经常使用几十年就因不合天而被废弃，使用寿命超过百年的屈指可数，这与历法推算中的表现精度完全不成比例。

在现代科学研究中，对精度的追求是一项系统活动，具体在对天体运行规律的把握中，需要观测精度、模型精度、计算精度的高度统一才能达到理想状态。古代历法家由于缺少误差思想的指导，在对观测精度远远没有达到、对天体运行的规律掌握尚有限的情况下，经常单纯追求计算的高精度，以求修成的历法“止于至善”。但实际上，古人在这方面付出的努力多为事倍功半，因为计算结果比计算本身更重要，没有意义的数字位数参与运算是一种资源的浪费。

本文以现代误差和近似计算思想为指导，对古代历法的误差思想空缺现象做初步的梳理和探讨，以期从这一不引人注意的角度进一步来加深我们对古代历法的了解和认识。

1 中历对“完美”天行的追求

中国历史上各朝频频改历，小部分是政治因素，大部分是“验天不合”或“不精”造成的。

在“天不变，道亦不变”思想的指导下，古人存在一种能够对天行“终极把握”的理想，认为天体的运行周期可以通约(至少在中古前是这样认为的)。战国秦汉时代的“四分历”，认为一回归年为365天，闰周为19年7闰，于是现代人根据这两个数值替古人推

在追求对天行终极把握理想的推动下，各朝历法都设法使其精度在前人的基础上有所提高，这种提高是符合科学精神的，但也由此形成了一种观念，认为历法就应该是一种不断改变的东西。甚至直到清初，引进西学，历法精度大幅提高时，著名历法家王锡阐仍说:“历之道主革，故无百年不改之历”［1］，把改变历法当成了常态。可是，由于天体运行的复杂性，使其运行周期找到通约的理想永远无法实现。中历是阴阳历，即使仅仅单纯考虑日、月两天体的运动，也无法找到一个理想的会合周期(如朔望月的发生原理非常简单，但每月的长度都各自不同，而且找不出这种长度变化的周期)，更何况其他天体运行周期的通约了。

于是古人试图寻找另外的途径作为补充，以辅助实现这一目标。我们的先辈很早就发现，乐律是有明显周期的，既然日长、年长都有周期，于是他们认为天体运行也会像乐律一样遵守简明的数理关系，因此从很早开始，历法就和乐律联系在一起，称“律历”，历法的某些参数需要符合黄钟、律吕之数;另外，根据古代根深蒂固的数字神秘观念，古人还认为，某些数字存在万能的功用，包含着万物之理，所以人们经常让历法的某些参数与一些神秘数字相合(如乾象、大衍之数等)。综合这些因素，古人认为一部完美的历法应该是既合天，又相合与乐律和神秘数字的。

随着时代的发展，观测精度逐渐提高，人们发现那种简单的通约关系(如“19年7闰”)并不能合天，但多数人仍相信天体运行周期是有通约关系的，只是更复杂而已。于是古人使用了一些更为“精密”的参数，如西汉《太初历》取一个朔望月为29日，东汉刘洪(约公元129～约210)的《乾象历》定回归年长为365日，南朝祖冲之(公元429～500)取闰周为392年144闰等等。这些数据包含有实测的成分，但也包含有靠乐律、神秘数来制造高精度的愿望，带有力求“完全精密”的理想主义的观念。

上元积年的使用是古人追求对完美天行把握的最典型体现。上元是古代历法家寻找的一个理想推算起点，他们相信，按照他们观测获知的日、月、五星的运行周期，叠加回推，最后总能找到一个理想时刻:这一刻是一个甲子日的夜半，又是日月合朔的时刻，又恰是太阳过冬至点，同时在冬至点发生罕见的“五星联珠”(即五大行星在视线聚集于冬至点准备出发)。正式推算上元积年的工作是从西汉的刘歆开始，他在《三统历》中一直推到143，127年前，才找到这个理想时刻。［2］后来随着交点月、近点月等周期的发现，这些参数也常被加入到历法的上元推算中去，随着各种参数的精密化，理想推算起点变得越来越难找，只好继续向远古推去，求出的上元积年的数字也越来越庞大，到唐代的《大衍历》达到96，661，740年(［2］，623 页)，金代的《重修大明历》更达到了 383，768，657 年(［2］，1266页)。

古人这么孜孜以求庞大的上元积年，除了基于天行完美的假设外，还有这样一种观念:想为历法推算、天体位置和天象的推算找到一个通用程序，真正达到孟子说的“千岁之日至，可坐而致也”［3］的随心所欲不逾矩境界。古代通常的演算方法是“筹算”，用摆放和移动算筹(小竹棍)来排列算式，非常费时费力，这样，太大的计算量就会成为历法家沉重的负担。

在对中国古代历法的研究中，推算上元积年的方法因为涉及解一次同余式，是数学史上的一大贡献，被大加赞赏，但因其推算的思想不甚“科学”而经常被忽略或淡化。实际上，推算上元积年从方法和思想上都是古代历法最核心的内容，它可以解开历法中的很多谜团。陈遵妫曾说:“一部中国历法史，几乎可以说是上元的演算史。”［4］上元积年的确定需要同时考虑许多长短不齐的周期，尤其是这些周期达到小数点后许多位的精度时，回推上去想找到一个共同的“起跑线”，具有非常高的难度，精确的位置恐怕永远也找不到，今人研究发现，古人设定上元时并不完全是客观运作的。

曲安京经过研究证实，古代围绕着上元积年的计算，存在着一个天文常数系统，推导上元积年时只用60干支周期、朔望月和回归年长度进行推导。如果布列的同余式组无解，或求出的上元积年超过1亿年，说明取的朔望月和回归年长度“不合用”，需要用何承天调日法“设计”新的朔望月和回归年长度，再重新计算，若所得结果小于1亿年，说明该上元符合要求，于是定出上元和上元积年。至于恒星年、近点月、交点月、五行星会合周期等数值，按这亿年数量级的尺度作出调整，总是能找到一个既满足上元起点、又非常符合今日位置的长度周期的。［5］①这是关于中国古代历法的一个重大发现，关系到历法制定和推算本质的全局问题，也是关系到历法精度的重要问题，是涉及整个“森林”生态而不是只考察某棵树木的问题，但一直没有在学界得到广泛的重视。且不说取朔望月和回归年长度也靠改换数字、闭门造车来迁就理想上元，就说恒星年、近点月、交点月、五行星会合周期等数据在上亿年的漫漫历史长河中一分配，虽然得到一个与当时观测长度相近的值，但有没有误差，误差究竟是多少，就无法再去考虑了，结果这些参数仅符合了当时和较近的过去，行用日久必然会不合天。

古人确定上元积年时，还常求出理想上元的“总周期”，即上一次上元完美天象到下一次重复出现的时间间隔，其数字更为庞大，据高平子研究，后汉四分历的总周期年数有18位，远远超过今日“大爆炸宇宙学”设定的宇宙年龄，故这种周期大数，根本没有任何实际意义。有人认为上元的确立说明古人有宇宙学的“开辟”思想，高平子曾尖锐指出:即使真有一个气、朔、日月五星的“上元起点”，也不过是视象的会合，与一个原始的出发点是两回事，所以这种“开辟”思想离科学很远。［6］

上元积年本来是一种良好设想，但后来在历法推算中，历算家们常过分执着于这种设想，就成了一种对理想精度不切实际的追求，在这种追求过程中，历法家不惜削足适履，将那些本该完全靠实测求出的天体运行周期安排成“导出常数”，但其实际意义与现代天文学中的“导出常数”完全不同。由于古人不了解误差出现的必然性和使用近似计算的必要性，所以这种追求完美的结果反而更不完美——历法几十年一换。

元代的李谦(1233～1311)在《授时历议》中曾对上元积年，以及其中的人为运作有过这样中肯的判断:“昔人立法，必推求往古生数之始，谓之演纪上元。当斯之际，日月五星同度，如合璧连珠然。惟其世代绵远，驯积其数至逾亿万，后人厌其布算繁多，互相推考，断截其数而增损日法，以为得改宪之术，此历代积年日法所以不能相同者也。然行之未远，浸复差失，盖天道自然，岂人为附会所能苟合哉。”(［2］，1360页)

由于后世历法家的质疑，到中、近古，经唐宋时代的曹士蔿、杨忠辅等作了尝试性的改革以后，元代郭守敬(1231～1316)在创制《授时历》中彻底废除了上元积年。

清代学者王锡阐(1628～1682)在评价一部历法的优劣时，曾提出这样的原则:“合则审其偶合与确合，违则求其理违与数违，不敢苟焉以自欺而已”。(［1］，607页)上元积年的凑数字，就有一种求偶合的倾向，用这种方法产生的历法，也难以达到真正的确合，结果造成理不违而数违。

2 中历里观测精度、模型精度、计算精度的不统一问题

在追求对天行完美把握观念的指导下，古代历法家对误差观念十分模糊，特别是唐代以前，只用绝对精确的数字——整数和分数来表示天体运行的各种周期及其关系，计算时也尽可能追求绝对的精度。实际上，计算只是历法编制的一个方面，从科学的角度讲，只有做到观测精度、模型精度、计算精度的统一，才能编制出一部好的历法来。

按现代误差理论，在科学研究中，定量的误差主要有3种:

(1)观测误差。就天文观测来说，测量仪器、测量方法、测量人员的因素，都会产生误差。仪器的安装准确程度、刻度盘(尺)的调准程度、刻度精密程度，瞄准的精确程度、读数的精确程度对误差的产生都有重要影响，我们只能将其控制在一定范围内而不可能将其彻底消除。

(2)模型误差。就天体运行模型来说，古人对日、月、五星的运动描述时总是进行抽象简化，往往没发现或忽略掉次要因素，如对行星的南北向运动、早期对天体的不均匀运动等，这样得到的数学模型只是近似描述。

(3)截断和舍入误差。在作天体位置推算的过程中，用数值方法求的总是近似解，比如用有限过程逼近无限过程只能取有限项，计算过程的四舍五入、取不足或过剩近似值等。这些误差积累起来也是很惊人的，这是计算方法造成的误差，又称方法误差。

我国古代，对天体位置、运行以及相应时间的测量精度如何呢?随着测量仪器的出现、完善，以及测量方法的不断改进，测量的精度也在随着历史的演变逐渐提高，但其精度与同时代的“计算精度”相比，总是非常低的。

最早出现的天文仪器是圭表和浑仪。圭表由直立的表(用来生成日影)和水平放置、朝向正北的圭组成，圭上标有刻度，当正午时，表的影子恰好完全落在圭上，通过圭上的刻度可以直接读出影子的长度。开始人们是寻找正午影子最短的一天，这天即为夏至，两次夏至的间隔即为一年［7］。

冬至是一年中正午影子最长的一天，测量冬至表影同样可以确定年长。后来人们改为主要测、甚至专测冬至表的影子长度来确定回归年长了。测量冬至日影就需要把圭的长度大大增加，至少在汉代，圭表已经定型为“圭”长于“表”的制式。《三辅黄图》中记载:“长安灵台……有铜表，高八尺，长一丈三尺”［8］，测量冬至影长也成为定规。对这种改变的原因，典籍中没有记载，按现代误差理论，用同一方法测量长的样本时，比测量短的样本会获得更高的精度，因为样本越长，读数的相对误差就越小。古人可能也是这么想的，这是古人改进测量精度的良好愿望，被后代认可，所以沿用下来，直到清末。

但实际上，这种改进不但没有提高测量精度，而且适得其反，降低了测量精度。日影长是一种特殊的样本，并不遵循“样本越长，读数的相对误差就越小”这一规律。具体地说，一个物体的影子越长，其影端由于太阳圆面造成的半影带就变得越宽，模糊的区域会按比例增加，所以与测量短影相比，测量长影并不会改善测量的相对误差。而对于圭表来说，由于冬至投影的倾斜角相对于夏至来说大大减小，会进一步加剧影子的弥散，使半影带在圭面上变得更宽，测量的相对误差精度不但不会维持在短影的水平，相反会降得更低。例如在北京，太阳冬至投射角约为26.5°，夏至为73.5°，取二者余弦的倒数之比，可知圭面上冬至半影的弥散度是夏至半影弥散度的3.2倍。据笔者对北京古观象台复原的郭守敬八尺铜圭表的多年观察，冬至前后，中午投射在圭面上的表影非常模糊，从正上方拍得的照片看，影缘若有若无，很难确定其位置，而夏至的表影则要清晰得多。后世长圭的圭表除了用于冬至测影外，当然还可以测量各节气的日影长度，这是非常必要的，但就利用圭表专门测量冬至影长求回归年这一点来说，这种技术“改进”实际上是一种倒退。

鉴于这种测冬至影长的传统，直到元代以前，圭表测影的精度一直很低，直到郭守敬发明景符后，利用针孔成像原理获得清晰的影端，测影长的精确度才明显提高。北京古观象台在1985～1986年，利用复原的郭守敬八尺铜表，加上景符进行不间断的仿古模拟观测，测得夏至前后影长误差值为0.1～0.2厘米，冬至前后误差为0.4～0.7厘米。［9］这也证明了我们上文的分析:使用景符，冬至日半影模糊带成比例增加的难题被克服了，但不同投射角造成的弥散度问题依然存在，因为圭面上冬至半影的弥散度是夏至半影弥散度的3.2倍，所以才有仿古模拟测影的上述冬、夏至误差值的差别。

据郭盛炽等人利用元代高表加景符的模拟观测，发现其误差平均也在0.47厘米左右，［10］与北京古观象台的模拟测影精度相仿，看来使用景符可以获得一个较高、较稳定的绝对精度，但不知古人是否意识到，即使采用景符，测量冬至影长的误差仍远远高于测夏至时的误差。

在有可以实际测量的圭表以前，年长的数据精度非常之低，《尚书·尧典》中提到一年的长度为“期三百有六旬有六日”，［11］这不仅是举成数，也是测的不准，日下余分是未定之数(［6］，90页)，等于只准确到“天”。由于圭表的观测目的是求出冬至时刻，进而求出回归年长，前者难以达到较高精度，因为冬至不一定恰好在正午，即使发生在正午前后，也不易判定其细小的偏差，但古人掌握了用多年测量求平均数的办法来改进年长数值，以求达到较高精度〔刘宋时代何承天曾“立八尺之表，连测十余年”(［2］，1083页)〕。“四分历”的回归年长为365日，精度相对提高了很多，应是由圭表多年连续观测获得。东汉刘洪的《乾象历》，取年长为365日，更接近了我们现在知道的回归年长度。以后各朝一直到元明，回归年长的精度逐渐在提高，但比起同时代算术的发展水平和计算精度，仍然是很低的。至于测冬至的时刻，精度则一直很低，南朝宋何承天测冬至的误差在50刻左右，随后祖冲之采用在冬至前后若干天测影长，再用比例归算的科学方法，测冬至的误差仍有20刻，宋代误差为10刻，元代郭守敬发明高表、景符，才使冬至测定的误差降到1 刻。［12］

东汉四分历中对五星会合周期的测定，木星误差为55分，土星47分，水星6分，火星则达到581分，数据内部这么大的差别，已经失去了统计学意义。到中古时代，五星恒星周期的测定误差比较稳定，也仅是在1刻上下。(［12］，398～399页)

浑仪是按照浑天说宇宙体系，将地平、子午、赤道、黄道、四游等圈环嵌套组成的“法象为器”式的天文仪器，观测者通过照准天体，可以利用环圈上的刻度来测量天体的坐标位置。在读数上，清以前浑仪的精度一直处在一个很低的水平。唐和唐以前的仪器都以“度”为最小单位，观测时仅可精确到半度，［13］北宋期间才出现了度以下的单位“少”(1/4度)、“半”(1/2 度)、“太”(3/4度)，［14］元代郭守敬的简仪，刻度刻到 1/10 度，可以估量到1/20度。(［14］，86页)由此可见，大多数朝代，还是停留在“一度少弱，一度少强”的水平上，据研究，宋及宋以前的仪器观测精度在某种意义上甚至不如目视直接估测的精度。［15］

古代已经有人意识到了仪器的测量误差问题，明代礼部尚书范谦曾说:“历家以周天三百六十五度四分度之一，纪七政之行，又析度为百分，分为百秒，可谓密矣。然浑象之体，径仅数尺，布周天度，每度不及指许，安所置分秒哉?至于臬表之树，不过数尺，刻漏之筹，不越数寸，以天之高且广也，而以尺寸之物求之，欲其纤微不爽，不亦难乎?”(［2］，1468页)表明当时人对仪器测量精度的怀疑。可惜没有人把它与天体运行模型，以及计算程序的精度联系起来考虑。

至于漏刻测时，误差也很可观。汉代漏刻至少有1/3刻的误差，到元代《授时历》才提高到1/20刻。(［12］，205～210页)时间的测量是“牵一发而动全身”的事，其误差对观测数据、计算结果都会有重要甚至层层放大的影响。陈美东曾指出:漏壶测时如果差一刻，那么测量太阳行度的误差就会有3.6度。(［12］，90页)现代误差理论证明，起始数据冬至时间的测定误差如果是一刻，那么无论用什么精密方法进行的历法推算，其预报结果的平均精度也不会比一刻更高。

而且，今人研究有时得出的古人观测精度也是虚假的。如唐梁令瓒在公元732年测的黄赤交角为24度，只精确到“度”，但被今人换算成现代度数，就成了23°39'57″，仿佛精确到了秒，然后与现代推算的当时黄赤交角理论值23°36'20″比，只差3'30″，于是虚假的精度就出来了。(［12］，99页)其实“24度”这值说明其精度不会好于1/2古度。

《后汉书·律历志》引《石氏星经》的话，提到黄道轨“去极百一十五度”，这也不过是个精确“度”的值，但经今人手里点化:一个象限弧为365度÷4=91度，115度 -91度=23度，化成小数，就成了23.6875度，［16］“去极百一十五度”成了精确到小数点后4位的数。实际上古代是到唐中叶才有十进小数的(以前只是偶见用十进制度量衡单位表示的类似小数的数目)，古人很可能以为他们那“去极百一十五度”是完全精确的，不知什么是“精确度”，更谈不上精确到“小数点后4位”。

古人的历法活动被后人赞为“先以密测”，“继以数推”。(［12］，30页)模型精度是与观测精度紧密关联的，没有精密的观测结果，就没有建立精确模型的基础，也发现不了旧有模型的偏差。中国描述天体运行的模型是“代数体系”——这个所谓“代数”，实际方法是根据一定间隔的天文观测，将观测数据列表，在了解了天体的运行周期和盈缩后，据此辅之以内插等代数方法来预测天体的位置，其模型多是直接来自观测数据的经验外推，只考虑视运动，并不究其几何关系。何况，较低的后续观测精度至多也只是改良一下过去的方法而已，难以发现旧模型的问题，因此这样的“继以数推”就大为可疑了。由于中国古典数学体系的非逻辑思维特性(主要通过直觉、想象、类比、灵感等思维方式解决数学问题)，影响到历法模型上，就少有改进和证伪的潜力，虽然有一次、二次内插法等创造，但总的来说，古人更重视推算的准确性而非天文模型的合理性，不重视对对象的解释，结果严重影响了模型的精度。比如，用“写子换母”方法修改数据，定好上元再确定一些天文周期，这都会严重影响对天文模型的思考，也会大大降低模型的精确性。

隋代刘焯(公元544～610)首次把太阳的不均匀运动引入历法推算，这在历法史上是一个创举，值得高度肯定，因为这样做会使历法的精度大大提高，也为深入了解天体的运动打下基础。可是，刘焯设立的太阳不均匀运动的模型有些不可思议:冬至时太阳运行最快，然后减慢，又加快，到春分点前的开区间达到最快，过了春分点又突然改成最慢，然后又波动到了秋分……(图1)，即便考虑到古人不懂得动力学上加速必须是一个渐进过程这一原理，我们也难以接受这样大起大落的跳跃式“无级变速”模型。这种模型不像是观测所得，而更像是主观臆测，即使是观测所得，也说明观测精度太低，观测者把观测的“噪音”、误差都当成真实的太阳运动了。且不说它与今天观测到的太阳不均匀运动符合多少，只说这样一个丑陋的模型，刘焯还在用他发明的插值法精确地计算，结果只能是南辕北辙，从实用的角度来说，这种计算还不如不算。

图1 刘焯的太阳不均匀运动模型(引自文献［17］)

历代天文观测、天体运行模型的精度在以很有限的速度提高。与此相比，古人在历法的计算过程上一开始就追求高精度，而且越古，这种追求高精度的欲望就越强。唐及唐以前，天文历算一直使用分数，今天的历法史家经常把这些分数展成小数，然后把古人追求的精度随心所欲地定位在小数点后4位或7位上，实际上今人这样做还是低估了古人的理想主义，古人对天体推算的目标很可能是“绝对精确”，所以才使用分数，因为分数是实现这一目地的最好手段——用今天的术语说，分数的有效数字是无穷多位，有真正理想的精确度。

问题是，计算只是历法制定过程中的一个手段，它不是目的，计算的精确度应与所给数据的精确度相当，而算得数据的精确度应与结果的实际需要、或实际能观测到的精确度相当，否则，其精确度再高也是无效的。古人没有这些观念，所以常把他们计算数据的精度搞得与观测数据的精度非常不成比例。比如古代历法中有些数据，在计算中精度高的我们可以把它展到7位数，而观测得来的原始数据却是“加一度少弱，减一度少强”，这样计算得到的结果貌似极为精确，其实早被不精确的原始数据吞没淡化了，至于后续的观测验证，由于古代漏刻、浑仪的精度都十分有限，这些虚假结果的精度也很难用仪器“证实”或“证伪”。

所以说，古人用分数计算历法并不是一种单纯的求简心理(希望有个简单的分数，比十进小数省力)，而是有一种对绝对精确和完美的追求趋向。这是古人的理想，但是用今天的眼光来看，这实际是陷入了一个不注重误差的“误区”。

保存到现在最早的真正传世历法(不光历谱，也包括“七政”的推算)，是明钦天监大统历科编的《大明嘉靖十年岁次辛卯七政躔度》，其中所有的表格中，推算天体位置是宿度只精确到“度”，时间则精确到“刻”——这是真正可用的推算结果，至于计算过程中那么高的精度到此全部抹平了，又回到观测时的“一度少弱，一度少强”水平。明代尚且如此，再古的历法就更可想而知了。［18］明代礼部尚书范谦对此曾说:“其差在分秒之间，无可验者，至逾一度，乃可以管窥耳，此所以穷古今之智巧，不能尽其变与?”(［2］，1468页)

可以拿我们今日的科学活动与古代比较:现代科学技术在误差和近似理论的指导下，测量、模型和计算三者的精度可以在很高的水平上合理匹配。现在，卫星导航的时间准确度要求在±10纳秒之内，而原子钟完全可以做到这一点;对天体轨道的确定需要天文观测的精度达到10-3角秒，现代大型的专业望远镜也完全可以做到这一点。当然，现代的巨型电子计算机的运算可以达到极高的精确度，比如可以把圆周率计算到小数点后超过60万亿位(2011年IBM蓝色基因/P超级计算机计算结果)，但天文学家不可能用这样的圆周率去进行天体轨道的计算，因为就现有的观测、模型精确度来说，圆周率超出小数点后十几位的计算，对精度的提高已经没有任何帮助了。

到了清代，受西方历法体系、数学思想的冲击，加上对过去制定历法经验的积累、对历法思想的反思，历法家们对历法误差问题开始有了比较清晰的认识。比较有代表性的是王锡阐，他曾对历法误差问题做过较为系统的分析，他认为导致历法误差的主要原因，是制定历法的基本指导思想的失误，“当时亦各自谓度越前人，而行之未久，差天已远，往往废不可用，何也?是在创法之人，不能深推理数，而附和于蓍卦、钟律以为奇，增损于积年、日法以为定。”(［1］，592页)

同时，王锡阐提出误差分三方面:数差、法差和理差。其中数差是在“以人验天”过程中产生的，相当于测量误差;法差是在历法推算过程中因数学方法产生的，相当于计算误差;理差是由于对天体运行的固有规律未能穷究而产生的，相当于模型误差。不过，王锡阐只强调了测量误差，称“人明于理而不习于测”“器精于制而不善于用”“一器而使两人测之，所见必殊”“一人而用两器测之，所见必殊”“所测之时，瞬息必有迟早也”等，对理差只泛泛说“数非理也，而因理生数，即因数可以悟理”，(［1］，615、593页)而对法差基本没解释。事实上，法差，也即推算中的误差是古代历法推算中的很关键因素，也一直是被古今学者在相当程度上忽略的因素。当代学者在研究古代历法时，曾对历代冬至太阳所在宿度的测算作了详尽的误差分析，总结出了九种可能的误差，但主要考虑的是观测误差和模型误差，几乎没有考虑计算方法误差。(［12］，90～92页)

3 中历里理想化而不实用的高精度问题

由于古人缺乏近似值的科学概念和对误差思想的空缺，对观测精度、模型精度、计算精度的不统一认识不足，所以在历法计算安排上对高精度的追求经常只流于表面和一厢情愿。近、现代学者们对古代历法的研究，对古人观测、模型、参数制定的精度作了很多有益的探讨，证明历代以来，历法的精度越来越高，(其综合成果见文献［12］，180～184页)但很少有人从理论上分析历法计算过程中的精度、误差问题。本节主要以《授时历》为案例，以古代其他历法的部分事例为补充，通过历法中的某些具体计算过程来对此问题作一初步分析。

对误差问题的理性思考来源于在计算过程中对计算结果和原始数据比较的深刻认识，按说中国古代历法推算的“代数体系”本应及时发展出对误差问题的观念，但实际上，直到明末西法传入以前，古代历算家一直没有对误差问题有明确认识，包括元代郭守敬的《授时历》及其改换名称后明代沿用的《大统历》也是如此。日本学者中山茂曾对此现象说过一句意味深长的话:《授时历》是数值至上主义。［19］其意思很明了:授时历过分依赖数值方法，不关心天体的真实运动模型，也忽略了可能的观测误差，只沉浸在数值的精度中。其实不光《授时历》如此，以前的历法基本都如此。

在实用计算中，不掌握近似计算的规律会严重加大计算量，在手工计算的时代此问题尤其突出。对天体位置的推算，人们总是希望精度越高越好，但是时刻、天体位置度数的初始观测精度都很低，模型也远不能精确反映天体运行状况的条件下，不掌握近似计算就不止是“事倍功半”了，按笔者模拟推算的经验，不考虑近似计算时，计算量会多10倍甚至几十倍，而精确度毫无提高。古代的计算工具是算筹，运用算筹计算的速度很慢，想必很多时间都耗费在无意义的计算中了。

举例来看，北宋《仪天历》中的漏刻计算冬至后损益差:

将 n=93.7412 代入，得 G2=91.5844。(［12］，195 页)

其实只要保留二位小数=93.74，就可达到测得精度91.6，也就是说，没有必要用精确到4位的小数作数据，n取二位小数，就可得到精确至0.1度的结果，而计算量只有原来的几十分之一。

我们可以举一个普通的计算过程来说明这个问题:

例:求测量数据11.66的平方、立方。

查平方表11.662=135.9556;查立方表11.663=1585.242296

如果测得误差为0.01，测得数据为11.67，

那么11.672=136.1889;11.673=1589.324463

两相比较，测得误差仅为0.01时，求出结果的小数位就根本无用了。

追求绝对精确、又不懂误差原理时，经常会对计算过程中误差过大的数值浑然不觉。虽然古人在很早就有了类似“舍入”的计算记载，［20］但历法推算时对此常常认识不足，如南朝祖冲之在根据观测值计算冬至时刻的过程中，对时间值的31.86刻，计算的下一步就成了31刻，取了不足近似值，(［16］，90页)这样算出的结果必然无形中加剧了误差。

观测误差和模型误差在一系列的计算程序中可能会被传递、放大。如果数据的初始误差小、模型合理，某一步运算对后一步的影响较小，随着计算的继续进行，可使结果偏离真实位置的时刻来得较晚或很晚，较长久的计算结果仍是合天的。反之，如果初始数据误差本来就突出、模型偏差较明显，再加上计算程序中对误差过大的步骤浑然不觉(如不合理的舍入等)，一些步骤会对后一步的影响加大，会导致误差逐步积累，计算结果就远离了应有的答案，不是“先天”就是“后天”了。对此，曲安京曾一针见血地指出:“古代历算误差太高，很多殚思极虑、苦心孤诣的东西，都被淹没在误差中，使历法几十年一换。”［21］

《授时历》是中国古代历法的顶峰，下面我们就通过对《授时历》有关内容的分析，看一看在中国古代历法的顶峰时期，天文历法家对误差思想和近似计算认识到了什么程度。

《授时历》的确是中国古代最好的一部历法，清代历法家梅文鼎曾对《授时历》作出这样的赞叹:“《授时历》不用积年，一凭实测，故自元迄明，承用三四百年无大差，以视汉、晋、唐、宋之屡差屡改，不啻霄壤。故曰:《授时》集诸家之大成，盖自西历以前，未有精于《授时历》者也。”［22］《授时历》从元朝至元十八年到至正二十八年(1281～1368)，共用了88年;明代沿用《授时历》，改名《大统历》，从洪武元年(1368)到南明小朝廷1662年，元、明共用382年，是历代历法中使用时间最长的一部。

但是，即使是在这样一部优秀、自觉摈弃了完美主义上元积年观念的历法中，对误差思想和近似计算也是相当忽视的。试举几例来看:

载于《元史·历志》的《授时历》以365.2425日为回归年，每百年减少0.0001日(明《大统历》废弃了岁实消长，即每百年减少的部分)，以365.2575度为周天(相当于恒星年)，以上的精度都是万分之一日。

而朔望月(朔策)是29.530593日，精度提高成百万分之一日，交点月(交终)27.212224日，精度也是百万分之一日，近点月(转终)27.5546日，又降回万分之一日，精度各不相同。这样在计算过程中，实际上精度高于万分之一日的部分根本无效，一般情况下仅起到加大计算量的作用。

对回归年的分割更能说明问题。《授时历》中一年的节气长是这样确定的:气策==15.2184375日，精度居然高到千万分之一日，这是在回归年(岁实)=365.2425000日的假设下得出的，而那时对回归年的测定不可能会到这样高的精度，所以节气长(气策)这样的高精度只有“数值至上”的意义而没有实用意义。

还有，在对太阳不均匀运动的校正计算中，取“缩初盈末限”春正至夏至为93.712025日，冬至至春正为88.909225日，也都比“基本常数”岁实的精度毫无必要地高了100倍。

在步日躔具体计算中有这样的算式:

每日定行度=四正后每日行度±日差

计算时，原有的基数(行积度)取小数点后4位，“每日行度”取小数点后6位，“日差”则取小数后7位，精度不一，前后差了1000倍，相加时后者的高精度完全被前面的低精度吞没。(［22］，656、660 页)

计算月行疾迟时有同样的问题:

初限损益分=定差0.1111-平差0.000281-立差0.00000325

=0.11081575

三项的精度也差了1000倍，如果第一项稍有误差，后两项，尤其是第三项就会变得毫无意义。(［22］，673页)

对于月平行度(每天运行的度数)，《授时历》取的是13.36875度，比周天度365.2575的精度也高了10倍。在“步交食”的推算中，月平行度取13.36875度，而交终度取363.7934度，正交度又取357.64度，日食阳历限取6度，精度愈来愈低，如果一个算式以上几个值同时出现，其结果只能准确到“度”，可谓极度的不精确了。(［22］，663页)

“步五星”中也有类似的问题，如木星动态，“平度”数据有精确到小数点后2位的，有小数点后5位的，限于篇幅，不再详细列举。(［22］，684页)

这些事例都说明，在中国传统历法中，即使最顶尖水平的历法家，对误差和近似计算观念也是混乱的，古代一以贯之的“绝对精确”观念仍然占主导地位，否则这么多参差不齐的精确度无法用理性解释。

最后，我们再看一看著名的“弧矢割圆术”问题。

弧矢割圆术是中国特有的一种球面三角理论，是继先人的相似勾股术、沈括会圆术后郭守敬的一项杰出创造。弧矢割圆术在中国传统历算上的贡献和影响，史界早有定论，本文不再赘述，只在这里分析一下使用弧矢割圆术时郭守敬在误差思想上的一些空缺。

郭守敬在推演弧矢割圆术时，采用的一周天度数为365.2575度，周天半径为60.875度(弧矢割圆术中，线长度也用“度”)，后者是怎么来的呢?原来，他取圆周率π为3，这样365.2575÷3=121.7525，原文为“径121度七十五分少”，将“少”略去，近似为121.75，取其半就成了60.875度。(［2］，1479页)

在南北朝时，祖冲之已经把圆周率π的值计算到了小数点后7位，虽然这个结果几乎被后人忘记，但人们在进行有关圆周与直径关系的运算时还是经常使用比3更精确的3.14或3.1416。过去历法较少使用圆周率，而郭守敬不用则已，一用就用了最粗疏的古率3，这实在让我们感到不安，因为用3或用3.1416，此一项误差就达4.7%。圆周率的有效数字只有1位时，其他的数据再精确，有效数字再多，计算起来也是只增加计算量，计算结果的有效数位还是1位。求周天半径时，求出的121.7525已经偏差很大了，接着又把0.0025略去，只保留两位，除以2时又得60.875，保留3位——对精度的这些设定，实在是过于随心所欲了。

在随后的演算中，郭守敬又取黄赤大距为24度，与周天半径为60.875度相比，精度又陡降为“度”，按这不甚准确的周天半径和精度极低的黄赤大距推算，如图2，求出了OK即黄赤大股q=56.0268度，DK即黄赤大勾p=23.8070度。(［2］，1479页)

而郭守敬实测的黄赤大距本为23.90度，如利用此值，同时求周天半径时π取3.1416，经计算可得 q=53.2880度，p=23.2328度，郭守敬的值与之相比，误差太大。再用他求出的值算黄道各度下赤道度，亦即用勾、股，从弧度求弦、矢，会导致更大的误差。

在和白道有关的常数中，郭守敬又取黄白交角为6度，精度也降到了“度”。当白道降交点与春分点重合时，得出“半交”(最低点)在黄道外6度，在赤道内18度——郭守敬甚至不顾实测的数，无意中又把前人“通约”的理想搬到了黄赤、黄白交角上。(［2］，1346页)

有学者认为，郭守敬弧矢割圆术中的古率3是“会圆术”这个统一的单位系里独特的比率，而不是圆周率，因为无论是弧矢割圆术，还是更古的会圆术，都是近似公式，但其最后结果与用现代三角学方法求出的相近，在特殊点甚至与现代值完全相等。［23］那么，是否那些近似公式包含了π的修正值?近似公式抵消了3为“圆周率”的部分误差?但据笔者使用部分值验算，使用古率3是次要的，主要是会圆术、弧矢割圆术本身是近似公式，如果用现代三角法算，即使圆周率用3，其结果的误差仍小于授时历的方法;相反，弧矢割圆术用更精确的π值时，得到的值精度更高，可见古率3并没有起到修正作用。

郭守敬在弧矢割圆术中圆周率用3，一直为后人诟病。潘鼐也认为，授时历的误差不是弧矢割圆术方法的问题，是黄赤交角、圆周率欠准确［24］。在处理天体运行不均匀的盈缩问题时，对周期性变化的数值，其误差尚可能抵消，但对于很多运算，误差是会积累的，所以这么优秀的一部历法，用了三百余年后，在明末清初终于变得不可收拾，最后让位于西法。

细分析《授时历》中推算过程的缺憾，都不是“瑕不掩瑜”所能开脱的，本来是孜孜以求精密的天文历法计算上居然率意使用3为圆周率，不顾实测的数据把天体运行轨道交角定成“通约”式的理想状态，在同一算式中不同项的精度居然相差达1000倍，都说明历法制定者在对算法的认识上有着严重缺陷。

本文仅对古代历法在误差思想方面的空缺作一初步而粗陋的分析，难免挂一漏万。以往学者对历法的研究，多集中于重建历法的推算结构，而对其运算过程的误差、特别是误差思想重视不够，甚至在复原计算时也常不考虑误差和近似结果，无意中在继续重演古人的虚幻精度。重建古人的工作是必要的，但在重建的同时，利用现代科学理论为指导，高屋建瓴地了解古人的成就，则更为必要，就误差分析来说，如果我们在重建古代一部历法的演算结构时，同时对之作比较详尽的误差分析，想必我们会得到许多新的认识和发现，这应引起历法研究者的关注。

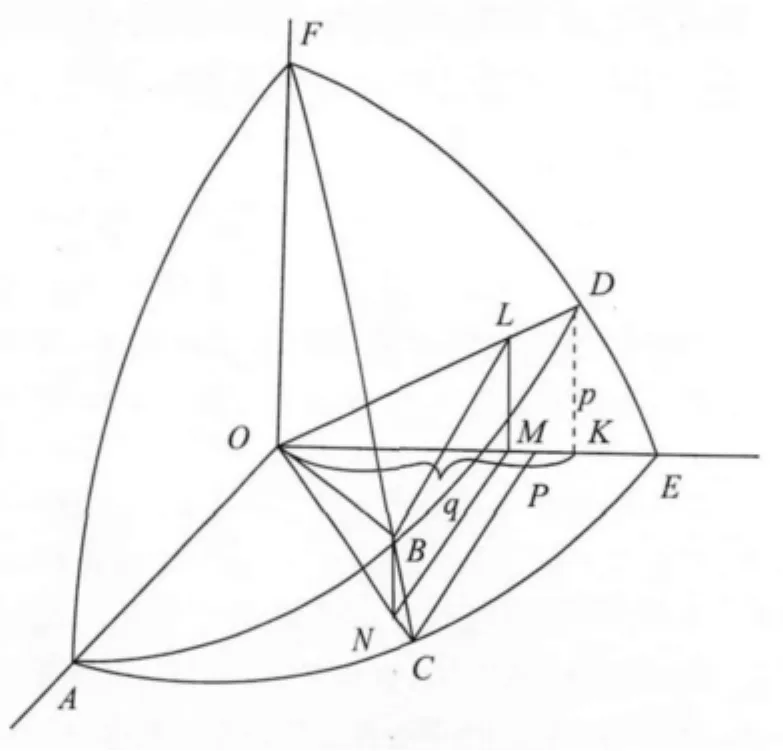
图2 弧矢割圆术的求黄赤道差和内外度图(引自文献［22］，629页)

1 薄树人.中国科学技术典籍通汇·天文卷［M］.第6册.郑州:河南教育出版社，1993.592.

2 薄树人.中国科学技术典籍通汇·天文卷［M］.第3册.郑州:河南教育出版社，1993.77.

3 孟子［M］∥四部丛刊初编.经部.第10册.卷8.上海:商务印书馆(缩印宋刊本)，1936.68.

4 陈遵妫.中国天文学史［M］.第3册.上海:上海人民出版社，1984.1391.

5 曲安京:中国数理天文学［M］.北京:科学出版社，2008.56.

6 高平子.高平子天文历学论著选［M］.台北:中央研究院数学研究所，1987.165.

7 伊世同.元代圭表复原探索［J］.自然科学史研究.1984，3(2):128.

8 何清谷.三辅黄图校释［M］.北京:中华书局，2005.279.

9 崔石竹，李东生.仿古测影探索［J］.自然科学史研究.1987，6(4):335.

10 郭盛炽.元代高表测景数据之精度［J］.自然科学史研究.1992，11(2):151.

11 尚书［M］∥四部丛刊初编.经部.第1册.卷1.上海:商务印书馆(缩印宋刊本)，1936.7.

12 陈美东.古历新探［M］.沈阳:辽宁教育出版社，1995.61～64.

13 潘鼐.中国恒星观测史［M］.上海:学林出版社，1989.140.

14 张柏春.明清测天仪器之欧化［M］.沈阳:辽宁教育出版社，2000.80.

15 王玉民.以尺量天——中国古代目视尺度天象记录的量化与归算［M］.济南:山东教育出版社.2008.46.

16 中国天文学史整理研究小组.中国天文学史［M］.北京:科学出版社，1981.96.

17 王荣彬.刘焯《皇极历》插值法的构建原理［J］.自然科学史研究，1994，13(4):295.

18 薄树人.中国科学技术典籍通汇·天文卷［M］.第1册.郑州:河南教育出版社，1993.709～715.

19 曲安京.一部撰写了40年的著作终于出版了［M］.中国科技史杂志，2006，27(3):270.

20 李俨，钱宝琮.李俨钱宝琮科学史全集［M］.第4卷.沈阳:辽宁教育出版社，1998.142.

21 曲安京.中国历法与数学［M］.北京:科学出版社，2005.178.

22 张培瑜，陈美东，薄树人，胡铁珠.中国天文学史大系·中国古代历法［M］.北京:中国科学技术出版社，2008.615.

23 邓可卉.授时历中的弧矢割圆术再探［J］.自然科学史研究，2007，26(2):162.

24 潘鼐，向英.郭守敬［M］.上海:上海人民出版社，1981.156～157.