秦淮河地铁桥物理模型试验研究

姬昌辉，洪大林，谢 瑞，申 霞

(南京水利科学研究院，江苏 南京 210029)

南京地铁一号线南延线秦淮河大桥(简称“地铁桥”，下同)在江宁天元中路段(简称“天元桥”，下同)下游跨越秦淮河，两桥净距离约25 m.地铁桥走向与河道基本正交，跨径47.5 m(边跨)+75 m(主跨)+47.5 m(边跨)，主桥墩采用双壁墩，墩厚1 m(在9.5 m以下墩厚为1.8 m)，墩宽4.7 m，两边墩(工字型桥墩)尺度分别为:宽1.8 m，厚2.3 m和宽2.5 m，厚3.2 m.天元中路秦淮河大桥全桥在河中设10座墩台，每个墩台设3 个圆形桥墩，直径为 1.4 m［1］.

地铁桥与天元桥距离较近，桥墩壅水会产生叠加效应，而且地铁桥的桥墩与天元桥桥墩墩型不同.现有关于桥墩壅水的经验公式研究较多［2－4］，但对壅水叠加的研究却较少［5］，并且经验公式受到具体适用条件的限制［6］，因此，研究桥墩对水流影响较为可靠的方法就是模型试验［7－10］.本文旨在通过物理模型试验确定地铁大桥对河道水流的影响程度，以及地铁大桥和天元桥对河道水流的综合影响，为大桥设计及防洪影响评价提供依据.

1 模型设计及模型验证

模型与原型除几何相似外，还需满足水流运动相似［1，11－12］:

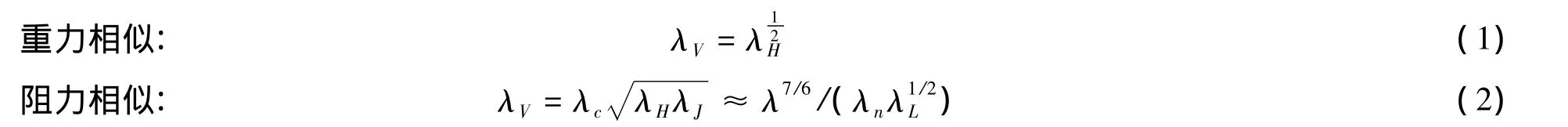
式中:λV为流速比尺，λH为垂直比尺，λc为谢才系数比尺;λJ为水力坡度比尺;λn为糙率比尺，λL为平面比尺.

秦淮河为宽浅河道，综合考虑河道水流特性及试验场地等因素，取平面比尺λL=100，模型水流应为紊流，临界雷诺数Rekp取1 000，桥位附近平均水深取6 m，水流平均流速取1 m，水的运动黏滞系数取0.01 cm2/s，模型垂直比尺需满足:

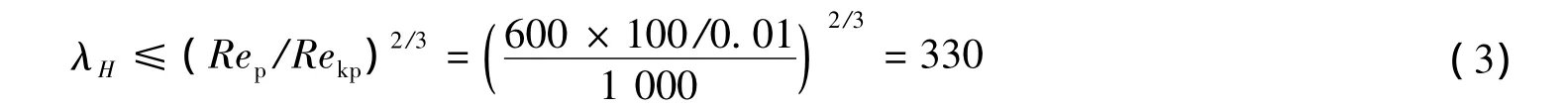
为使模型水流处于阻力平方区，垂直比尺需满足

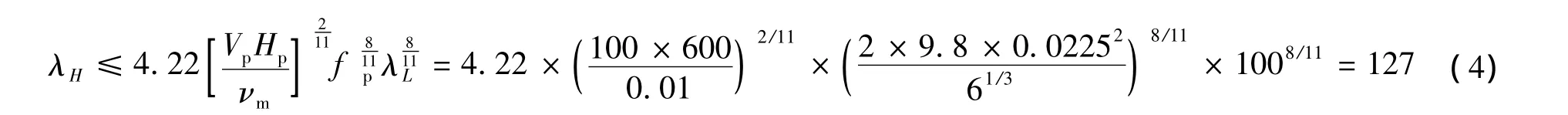
式中:天然河道的阻力系数fp=2gn2/R1/3.

因此选用垂直比尺λL=50可满足要求，流速比尺λV=7.071，糙率比尺λn=1.36，流量比尺λQ=35 355.本河段综合糙率取0.022 5，模型糙率为0.016 5.当采用卵石进行梅花形加糙时，可根据唐存本公式计算糙率［11］:

式中:A=16.6［1-3.0(d/L)+3.78(d/L)2-1.29(d/L)3］

选择d=1.0 cm卵石进行梅花形加糙，计算得其间距为16 cm，可满足模型糙率要求.模型模拟的范围选择为拟建桥梁上游1.8 km，下游1.0 km(模型布置见图1)，由于本河段缺乏实测水文资料，工程附近河段也无水文站(水位站)，上、下游水位站距工程地点均有较远的距离，因此无法进行实测资料下的模型验证，只能根据规划的水面线(50 a一遇洪水)及其实际行洪水面线(1991年)对模型进行验证.验证内容:①流域50 a一遇降雨遇长江20 a一遇潮位时，秦淮河流量1 603 m3/s，牛首山河流量30 m3/s，对应三汊河口水位9.96 m，主要验证牛首山河口(天元桥上游500 m)、牛首山河口向上1 km(天元桥上游1.5 km)、桥位、9+400处水位(地铁桥下游800 m);②1991年洪水，秦淮河流量1 354 m3/s，牛首山河流量23 m3/s，验证牛首山河口、牛首山河口向上1 km处、桥位、9+400处水位［1］.模型各水位站实测值与推算值基本相符(表1)，最大偏差在5 cm以内，满足定床模型试验的精度要求.

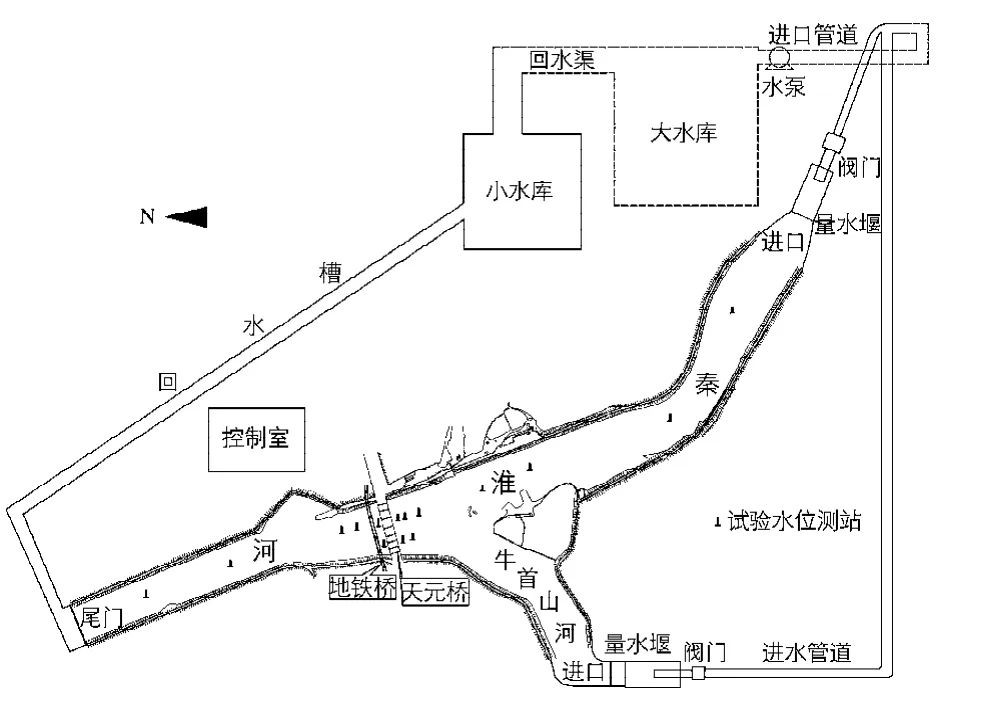
图1 模型布置Fig.1 The layout of physical model

表1 水位验证Tab.1 Water level verification m

2 试验内容及结果分析

2.1 试验水流条件

试验针对无工程(原始河道)、天元桥(河道中无地铁桥)、地铁桥(地铁桥及天元桥组合)3种工况进行，其放水条件见表2.

表2 模型试验放水条件Tab.2 Experimental conditions

2.2 水 位

河道沿程布置15个水位站(图1).在3种水流条件下，无论有无桥梁工程，附近河段的水面比降沿程变化(图2)基本上可以分为3段:天元桥上游1.5 km至天元桥上游1 km，河道较窄且伴随弯道，水面比降为1.2‱～2.6‱;由天元桥上游1 km至牛首山河与秦淮河汇流处，河道逐渐放宽，水面趋于平缓，其比降为0.6‱～1.0‱;由天元桥至下游800 m内河道又收缩变窄，水面比降相对较大，为2.2‱～3.3‱.

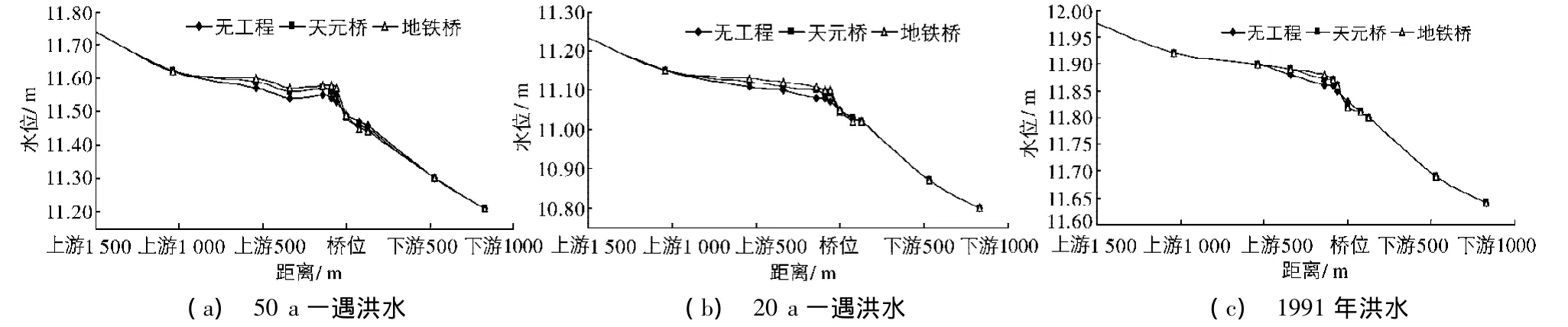
图2 沿程水面线Fig.2 Water surface profiles

地铁桥对河道行洪的影响可以分2个层次来分析:一是地铁桥相对天元桥(河道中仅有天元桥，下同)的比较结果;二是地铁桥相对河道无工程情况的比较结果.分析结果见表3.

表3 水位壅高值Tab.3 Level of backwater

2.3 流 速

地铁桥建成后，桥区附近的流速发生一定的变化，桥墩墩前到天元桥之间、桥墩墩后局部水域流速明显减小，墩间水流流速增大.建桥对河道流场的影响随着流量、流速的增大而增大.在工程方案试验的3种水文条件中，50 a一遇洪水水文条件下，工程对河段流场的影响最大;1991年洪水水文条件下影响次之;20 a一遇洪水水文条件下影响最小，影响范围在桥位上下游约400 m以内.

地铁桥建成前后桥位断面流速值见表4，桥墩墩前至天元桥之间、桥墩墩后流速有明显减小，墩间流速增大.影响最大为50 a一遇洪水的情况，地铁桥桥位处工程前最大流速1.88 m/s，工程后墩前15 m流速减小0.12 ～0.16 m/s，桥轴线断面左主墩两侧流速增大 0.03 ～ 0.29 m/s，右主墩两侧流速增大 0.03 ～0.25 m/s，桥下游两墩之间局部水域流速有所增加，墩后水域流速减缓，流速变化在－0.07～0.02 m/s.

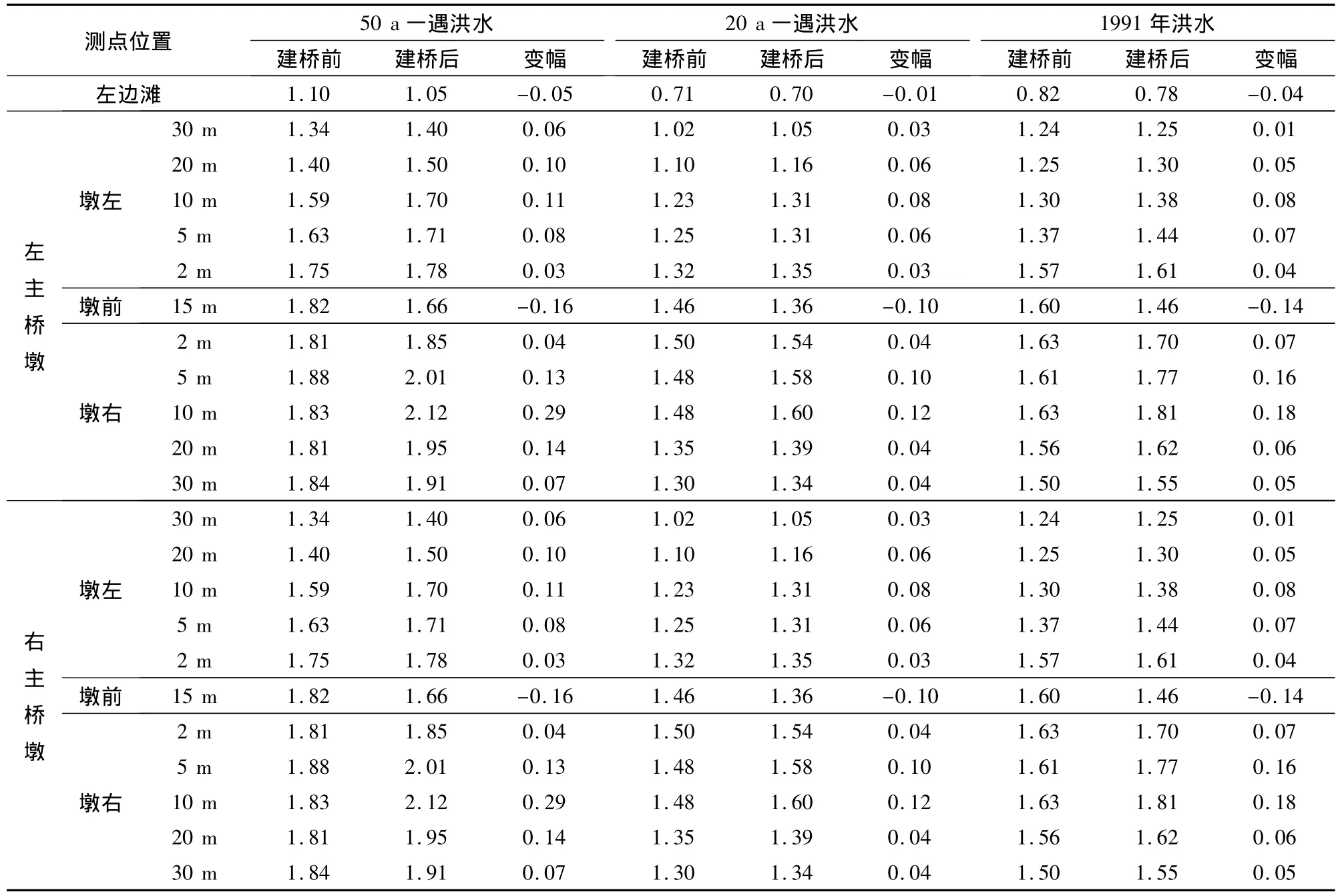
表4 地铁桥桥位处流速Tab.4 Velocity near piers m·s－1

2.4 流态

考虑到3级流量相差甚小，水位差也小于1.0 m，因此观察河道水流流态时，仅采用其中50 a一遇的流量为试验条件.

试验结果表明，水流在上游出弯道后，受右岸凸出部分的挑流后，向左偏离，同时右侧出现一大片回流区，回流区内出现上下两个回流，其中上游回流范围小于下游回流范围.水流在牛首河口与牛首河入流汇合，但由于牛首河汇流量相对秦淮河的流量甚小，几乎可以忽略，而河口区为一片开阔地带，水流在此受河道平面形态的影响产生大片汇流区(图3);水流在经过牛首河口进入下游天元桥河段时，已经基本平顺地与桥梁墩柱相衔接，即水流方向与桥梁墩柱方向基本平行(图3)，地铁桥的建成也没有改变水流的流向，桥梁的平面布置是合理的.

图3 流态图Fig.3 Flow pattern

2.5 桥墩壅水计算公式比较

本文采用3种桥墩壅水计算公式计算地铁桥、地铁桥与天元桥组合的水位壅高值，并与物理模型试验测量结果进行对比分析，3种壅水计算公式［2，6］如下:

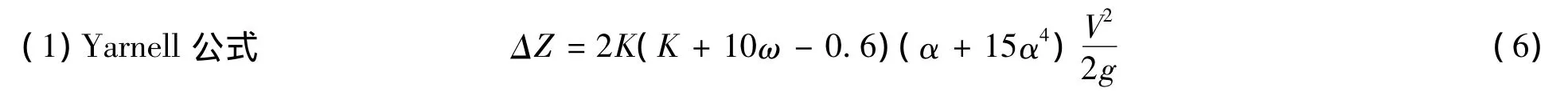
式中:ΔZ为水位壅高;K为桥墩形状系数，取值见表5［2，6］;ω=V2/(2gH)，V为桥下游断面流速，H为桥下游断面水深;α=A'/A为桥墩阻水比，A'为桥墩迎水面积，A为桥下游断面过水面积.

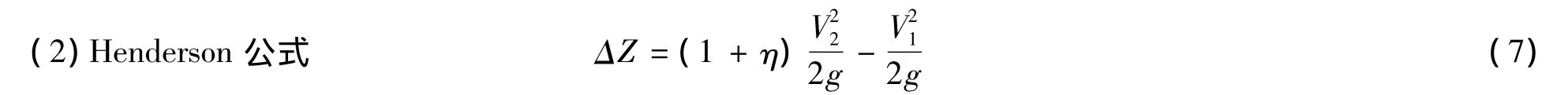
式中:η为与桥墩形状有关的Henderson系数，矩形桥墩取0.35，圆形墩取0.18;V1为桥前流速;V2为桥下流速.

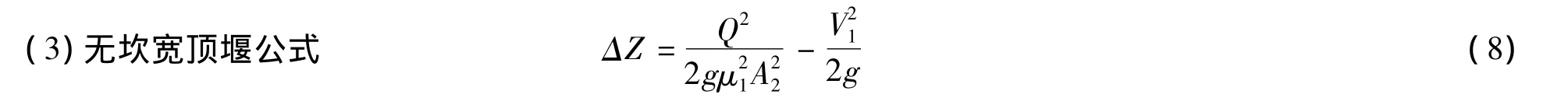
式中:μ1为流量系数，与桥墩墩头形状有关，取值见表5，其中σ=1－α，α为桥墩阻水比;A2为桥下过水总面积.

表5 桥墩形状系数K和流量系数μ1Tab.5 Shape coefficient K and flow coefficient μ1

地铁桥工况:桥墩为双壁墩和工字型墩，计算中桥墩按方形墩考虑，Yarnell公式中取桥墩形状系数K=1.25;Henderson公式中取Henderson系数η=0.35;由于桥墩阻水比较小，σ=0.95，因此利用表5中的流量系数进行外延，无坎宽顶堰公式中取流量系数μ1=0.92.

地铁桥与天元桥组合工况:地铁桥墩为双壁墩和工字型墩，天元桥桥墩为圆形状墩，计算两桥叠加影响时桥墩按方形墩考虑，Yarnell公式中取桥墩形状系数 K=1.25;Henderson公式中取 Henderson系数η=0.35;无坎宽顶堰公式中取流量系数μ1=0.91.

在3种水流条件下的桥墩壅水高度计算值见表6，与物理模型试验结果相比可见，Yarnell公式计算结果明显偏小，而Henderson公式偏大，相比之下，无坎宽顶堰公式计算结果虽然略有偏大，但最为接近，该公式是文献［6］经过与数学模型计算结果对比分析后给出的推荐公式.

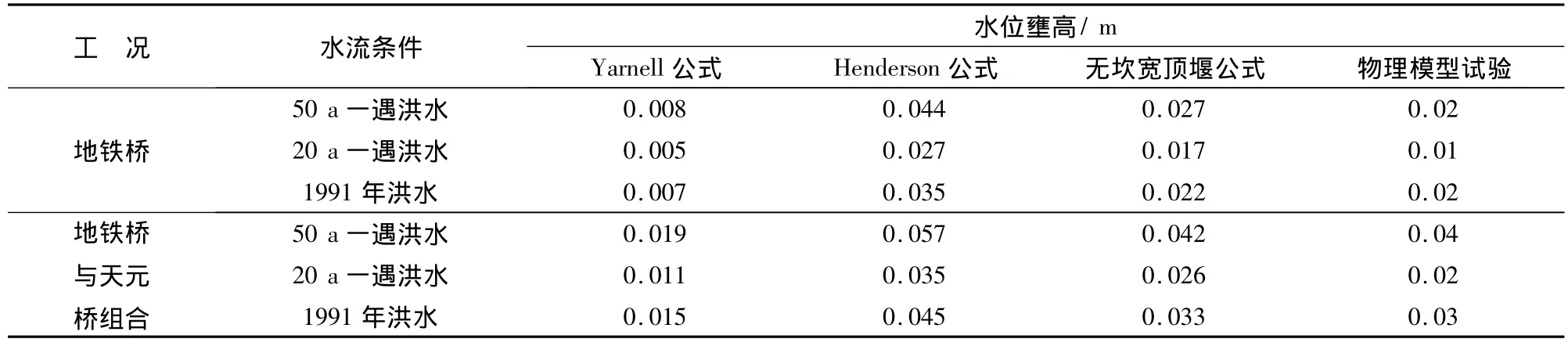
表6 水位壅高比较Tab.6 Comparison of backwater level

利用无坎宽顶堰公式进行计算仍存在如下问题:无坎宽顶堰公式适用于阻水比较大的情况［6］，对于阻水面积比较小的情况其流量系数采用外延的方法选择是否恰当仍需进一步研究;对于双壁墩和工字型墩等特殊的桥墩也没有给出流量系数;对于两座桥梁的桥墩完全不同的情况其流量系数如何选择等.因此与选用经验公式进行计算相比，采用物理模型试验的方法更为合理.

3 结语

(1)本段河道水面线呈现明显的三段特点，即牛首山河上游河道较窄，水面比降较大，牛首山河至天元桥段，水面开阔，水面平缓，比降较小，桥下河段河道变窄，水面比降增大.

(2)地铁桥对行洪水位的影响以50 a一遇洪水最大，其最大壅水范围为桥上游500 m，水位壅高0.02 m.地铁桥与天元桥对行洪水位的综合影响:50 a一遇洪水时影响最大，影响范围为上游500 m，水位壅高0.04 m.

(3)拟建地铁桥与水流方向正交，桥墩设置与水流方向一致，无需调整桥墩方向，另外，主桥墩设置在主槽两侧靠近边滩处，对河道行洪水流的影响相对较小，桥墩设置较合理.

(4)由经验公式计算的桥墩壅水值与物理模型试验结果对比可见，Yarnell公式计算结果明显偏小，而Henderson公式明显偏大，无坎宽顶堰公式相对较接近，但由于无坎宽顶堰公式适用于阻水比较大的情况，对于特殊的桥墩没有给出相应的流量系数，是否适用于多桥叠加影响尚有待研究等原因，因此采用物理模型试验等方法研究桥墩壅水更为合理.

［1］洪大林，姬昌辉，谢瑞.南京地铁一号线南延线秦淮河大桥工程物理模型试验研究［R］.南京:南京水利科学研究院，2007.(HONG Da-lin，JI Chang-hui，XIE Rui.Physical model test of Qinhuai River Nanjing Metro Bridge［R］.Nanjing:Nanjing Hydraulic Research Institute，2007.(in Chinese))

［2］王开，傅旭东，王光谦.桥墩壅水的计算方法比较［J］.南水北调与水利科技，2006，4(6):53-55.(WANG Kai，FU Xudong，WANG Guang-qian.Comparision of existing backwater models for bridge piers in subcritical flows［J］.South-to-North Water Transfers and Water Science＆ Technology，2006，4(6):53-55.(in Chinese))

［3］董耀华，宫平，黄煜龄.水力学方法估算大桥对河道防洪的影响［J］.长江科学研院报，1998，15(3):17-19.(DONG Yao-hua，GONG Ping，HUANG Yu-ling.Hydraulic methods for estimating effect of bridge on flood control of river channel［J］.Journal of Yangtze River Scientific Research Institute，1998，15(3):17-19.(in Chinese))

［4］谢理洲，卜海磊，刘英.郑州官渡黄河公路大桥的桥渡设计［J］.人民黄河，2009，31(9):96-101.(XIE Li-zhou，BU Hai-lei，LIU Ying.Aqueduct design for Guandu Yellow River Highway Bridge in Zhengzhou［J］.Yellow River，2009，31(9):96-101.(in Chinese))

［5］王开，魏加华，张成，等.桥梁分布特征对输水渠道过流能力的影响—以南水北调中线工程为例［J］.应用基础与工程科学学报，2009，17(3):327-334.(WANG Kai，WEI Jia-hua，ZHANG Cheng，et al.Effect to discharge capacity of channel from bridges distribution—a case study of South-North Water Transfer Midline Project［J］.Journal of Basic Science and Engineering，2009，17(3):327-334.(in Chinese))

［6］郭晓晨，陈文学，穆祥鹏，等.南水北调中线干渠桥墩壅水计算公式的选择［J］.南水北调与水利科技，2009，7(6):108-112.(GUO Xiao-chen，CHEN Wen-xue，MU Xiang-peng，et al.Formula selection on backwater effects of bridge piers for the Middle Route of South-to-North Water Transfer Project［J］.South-to-North Water Transfers and Water Science ＆ Technology，2009，7(6):108-112.(in Chinese))

［7］杨小亭，霍跃东，徐孝平.南水北调中线工程桥墩水力学试验研究［J］.武汉水利电力大学学报，2000，33(6):16-19.(YANG Xiao-ting，HUO Yao-dong，XU Xiao-ping.Hydraulic experimental study of piers for middle route scheme of South-to-North Water Transfer Project［J］.J Wuhan Univ of Hydr＆ Elec Eng，2000，33(6):16-19.(in Chinese))

［8］张慧，黎礼刚，郑文燕，等.武汉河段二七路长江大桥河工模型试验研究［J］.人民长江，2008，39(1):57-58.(ZHANG Hui，LI Li-gang，ZHENG Wen-yan，et al.River channel study for Erqilu Changjiang Bridge in Wuhan city by river hydraulic model［J］.Yangtze River，2008，39(1):57-58.(in Chinese))

［9］黄荣敏，陈立，谢葆玲，等.建桥对河流洲边滩的影响［J］.水利水运工程学报，2006(2):51-55.(HUANG Rong-min，CHEN Li，XIE Bao-ling，et al.Influences of bridge building on bottom land evolution in rivers［J］.Hydro-Science and Engineering，2006(2):51-55.(in Chinese))

［10］韩海骞，熊绍隆，朱军政，等.杭州湾跨海大桥对钱塘江河口水流的影响［J］.东海海洋，2002，20(4):57-63.(HAN Hai-qian，XIONG Shao-long，ZHU Jun-zheng，et al.The impact on the flow of Qiantang Estuary by the Hangzhou Bay Major Bridge［J］.Donghai Marine Science，2002，20(4):57-63.(in Chinese))

［11］李昌华，金德春.河工模型试验［M］.北京:人民交通出版社，1981.(LI Chang-hua，JIN De-chun.River model test［M］.Beijing:China Communications Press，1981.(in Chinese))

［12］左东启，王世夏，刘大恺.模型试验的理论与方法［M］.北京:水利电力出版社，1984.(ZUO Dong-qi，WANG Shi-xia，LIU Da-kai.Theory and method of model experiment［M］.Beijing:Water Power Press，1984.(in Chinese))