基于模拟退火和支持向量机理论的变压器故障诊断方法

于 虹 张永刚

(云南电网公司博士后工作站 云南 昆明 650217)

1 前言

对变压器运行状态进行可靠、准确、及时的评估具有非常重要的意义。油中溶解气体分析(DGA)方法已被广泛应用于变压器的状态评估。国内外学者提出了很多具有实用价值的准则，如IEC 三比值法、Roger比值法、Duval法等［1－3］。其中，IEC三比值法是目前最广泛应用的变压器故障诊断方法，但其边界过于绝对，容易导致误判，因而需将其边界进行模糊化以避免其缺陷。支持向量机是基于统计学习理论的结构风险最小化原理解决了小样本、非线性等问题，提高其泛化能力，从而能很好地处理电力设备故障诊断所面临样本不足的缺陷。但SVM方法中某些参数的选择对其分类的准确率影响很大，因此，对SVM参数的合理选择能获得较好的分类效果。到目前为止，对其最佳参数的选择没有一个很好的手段，现有方法在计算耗时和效果方面都不是很理想。因而，为了提高SVM算法的准确性并解决IEC三比值法边界过于绝对的问题，本文采用模糊理论将IEC三比值的边界进行模糊化，并利用模拟退火方法对SVM的参数进行优化与选择。本文提出利用模糊理论处理IEC三比值法的边界，并利用模拟退火确定SVM的参数，并将模糊化的样本训练SVM，从而进行变压器的故障诊断，即故障分类，这样可以降低盲目选择SVM参数对分类结果的影响并提高故障诊断的准确性，从而为变压器设备提供一种辅助决策手段。

2 支持向量机

支持向量机(SVM)是一种研究有限样本情况下基于统计学习理论的VC维理论和结构风险最小化原则基础上的新机器学习方法，这种方法利用核函数将样本映射到高维特征空间并在此空间构造最优线性分类超平面，以获得最大的推广能力［4］。假定(xi，yi)i=1，2，…，n，xi∈ Rd，yi∈ {－ 1，+1}为样本训练集，其中xi∈Rd表示d维的特征向量，yi∈{－1，+1}表示特征向量xi归属的类别，n为样本数。在非线性情况下，利用非线性变换φ(·)将样本集原空间进行转换，样本空间两分类问题表示为:

式中:ω是权值向量，b为偏差。

另外，考虑到某些样本会存在不能被上式的分类超平面正确划分。因而，引入非负松弛因子εi来规定最大分类间隔和最小错误划分样本。规则化常数C＇决定对错分样本错误的惩罚程度［5］。因此，求解最优分类超平面的问题被转变为:

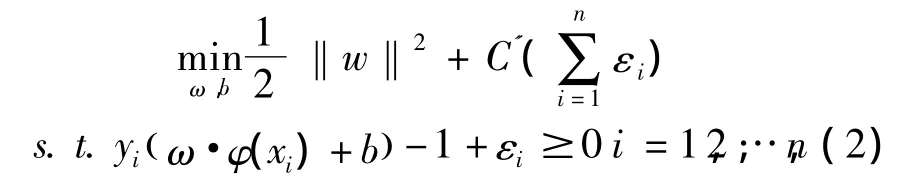
利用拉格朗日函数，式(2)转变为对偶问题进行求解:

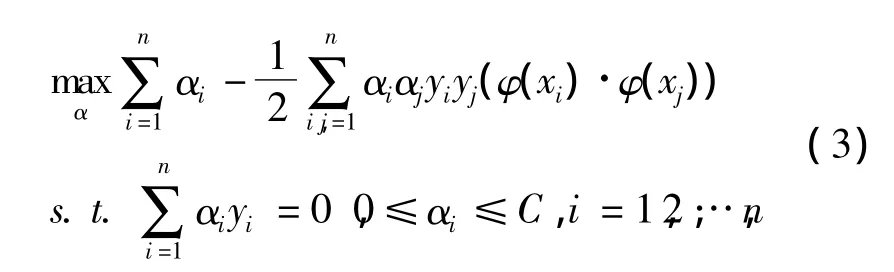
式(3)中，αi只有一小部分不为0，其对应的训练样本是支持向量，则最优决策函数:

上式中，K(x·xi)=φT(x)φ(xi)核函数，sgn为符号函数，结果为+1或－1，n是支持向量的数目，本文选取径向基核函数。规则化参数C＇和核函数参数σ的大小选择直接影响到SVM的分类准确性，因此合理的选取参数对SVM理论很重要。但SVM参数选取的现有方法都比较繁琐效果不好。因此，本文提出利用模拟退火(SA)算法获得SVM参数。

3 模拟退火算法

模拟退火(Simulated Annealing，SA)算法的思想是由Metropolis等提出的，Kirkpatrick等于1983年将其用于组合优化［6～7］。SA 算法是基于Monte Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法在某一初温下，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部优解能概率性地跳出并最终趋于全局最优。模拟退火算法应用的一般形式是:从选定的初始状态开始，在借助于控制参数T递减时产生的一系列“马尔可夫”链中，利用产生的一个新状态和接受准则，重复进行包括“产生新状态－计算目标的代价函数值－判断是否接受新状态－接受(或舍弃)新状态”这四个步骤的过程，不断对当前状态进行迭代，从而得到目标最优解。

在热力学平衡中，系统状态的概率分布服从所谓的 Boltzmas分布，即 Proch(E) ～exp(－E/KT)，其中E为表示目标能量的代价函数，T为温度，K为Boltzmas常数。这表明温度T的热平衡系统已在所有不同的状态E中将系统的能量做了概率分布，即使在低温状态下，也有机会使系统处于高能量状态。因此，有一个相应的机会使系统脱离局部能量极小，以利于找到一个更好的、更具整体性的能量极小。

总体说来，模拟退火算法中包含了两个循环:一个内循环和一个外循环。内循环就是在同一温度下的多次扰动产生不同状态，并按照Metropolis概率接受准则接收新状态，因此内循环是以状态扰动次数加以控制的。外循环包括温度下降的模拟退火(退火率r加以控制)、算法迭代次数I的递增和算法停止的条件，因此外循环基本是由迭代次数控制的。

在判断新状态是否被接受的一个最常用的接受准则是Metropolis准则

其中，ΔE是当前状态和新状态的代价函数值差，T为温度，模拟退火算法的流程见图1。

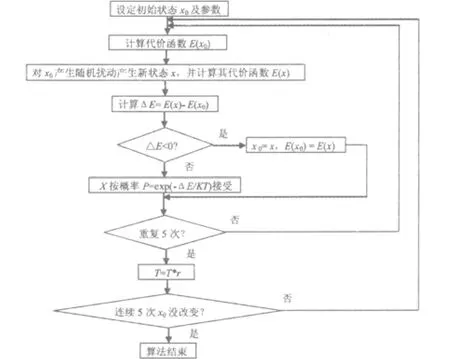
图1 模拟退火算法流程图

4 故障诊断模型

故障诊断模型采用模糊理论对传统IEC三比值法进行模糊化以避免其边界过于绝对的缺陷，利用模拟退火较快、准确地获得支持向量机的参数来实现对变压器准确、可靠、快速的故障诊断。

4.1 输入量及模糊化

IEC三比值法是常用且广泛使用的DGA方法。通常判断变压器油中H2、CH4、C2H6、C2H4和C2H2的三比值来判断其故障类型，IEC三比值法的编码规则如表1所示。

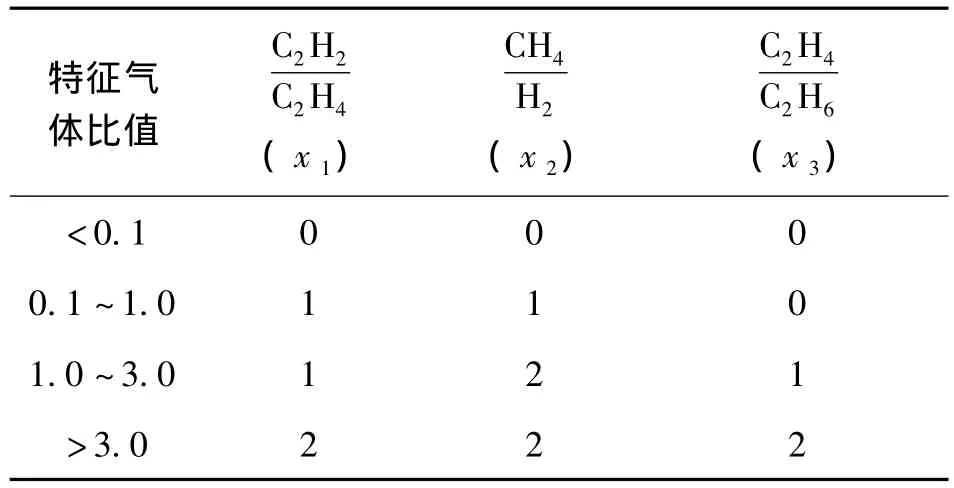
表1 IEC三比值法的编码规则

IEC三比值法的边界过于绝对，容易造成诊断的误判断，根据表1 IEC的编码规则及其变量的连续变化性，本文利用模糊理论中的隶属函数对其进行预处理，IEC三比值法的变量x1、x2和x3。分别在边界0.1和2的隶属函数如下所示。

将经过模糊预处理的IEC三比值变量x1、x2和x3作为支持向量机方法的输入量。

4.2 模拟退火确定SVM参数

本文利用模拟退火优化算法确定SVM参数C＇＇和σ来提高支持向量机分类准确性，SA其具体优化与确定参数过程如下:

Step1:给定初温T=3，退火率r=0.95，迭代次数I=5，随机产生初始状态x0，并计算相应代价函数值E(x0)。

Step2:对当前状态x0进行随机扰动产生一个新状态x，并计算相应的代价函数E(x)，从而得到ΔE=E(x)－E(x0)。

Step3:若ΔE＜0，则新状态x被接受;否则，新状态x按概率P=exp(－ΔE/KT)进行接受。当状态 x被接受时，将 x0=x，E(x0)=E(x)。

表2 变压器的故障集

Step4:在温度T下，重复一定次数(Markov链长度)的随机扰动和接受过程，即重复Step2与Step3，本文为重复5次。

Step5:缓慢地降低温度T=T*r。

Step6:重复步骤Step2～Step5直到连续5次x0没有改变为止。

4.3 SVM训练样本并获得变压器诊断结果

IEC三比值法变压器故障类型共有8类，需设计8*(8－1)=56个两类分类器。本文利用200组数据对SVM模型进行训练，然后用10组数据对已训练好的SVM进行验证，并与IEC三比值方法的实际故障诊断结果进行比较如表3所示。

表3 不同方法的诊断结果比较

5 结论

基于模拟退火和支持向量机理论的变压器故障诊断方法，不仅利用了模糊理论的隶属函数对IEC三比值法的边界进行模糊化以避免其边界过于绝对而造成诊断结果的误断，且通过模拟退火SA优化确定SVM参数，从而缩短了故障诊断的时间并提高了对变压器故障诊断的准确性，为变压器设备提供一种辅助决策手段。

［1］“Guide to the interpretation of dissolved and free gasses analysis，” IEC Std.60599，IEC Publication 60599，March 1999.

［2］R.R.Rogers，IEE and IEC codes to interpret incipient faults in transformers using gas in oil analysis，IEEE Trans.Electr.Insul.，vol.EI－13，no.5，pp.348～354，October 1978.

［3］M.Duval，Dissolved gas analysis:It can save your transformer，IEEE Elect.Insul.Mag.，vol.5，no.6，pp.22～27，1989.

［4］李凌均，张周锁，何正嘉.支持向量机在机械故障诊断中的应用研究［J］.计算机工程与应用，2002，vol.38，no.19，pp.19～21.

［5］邓乃扬，田英杰.数据挖掘中的新方法－支持向量机［M］.北京:科学出版社，2004.

［6］N.Metropolis，A.Rosenbluth，and M.Rosenbluth，et al.Equtation of state calculations by fast computing machines.Journal of Chemical Physics，vol.1953，no.21，pp.1087 ～1092.

［7］S.Kirkpatrick，Jr.CD.Gelat，and MP.Vecchi.Optimization by simulated annealing.Science，vol.1983，no.220，pp.671～680.