结合分段三次多项式与Akima法的等高线平滑方法

郑凤娇

（武汉市勘测设计研究院，湖北 武汉430022）

结合分段三次多项式与Akima法的等高线平滑方法

郑凤娇

（武汉市勘测设计研究院，湖北 武汉430022）

实际地形一般是连续变化的。根据数字高程模型（Digital Elevation Model，DEM）自动绘制的等高线由折线段相连而成，需要进一步平滑，以便更准确地描绘出实际地形的分布。结合分段三次多项式与Akima法来对等高线进行平滑处理。实验证明该方法效率高，结果满意，达到较好的平滑效果。

等高线平滑；分段三次多项式；Akima

等高线是地面上高程相等的一系列相邻点所连接成的曲线。它可以表示地貌的基本特征，是地表形态的一种主要表现手段，在地形模拟、道路勘测规划、水文模型建立、自然资源管理等地学领域存在许多优越性［1］。随着测绘技术的飞速发展，航测仪器从传统的模拟型到解析型，再到现阶段的全数字摄影测量工作站，同时，等高线的绘制方法也发生了根本性的变化，从手工绘制到半自动绘制，再到全自动绘制［2］。如果能通过计算机绘制出与作业员手工相似的等高线，这样将会大大缩短制作时间，提高生产效率。

在测绘生产中，如果已经具有数字地面模型DEM，可以根据一定的等高线跟踪算法进行等高线的自动绘制。等高线跟踪得到的是一系列分布在格网边上的离散等高线点，等高线的绘制是由这些离散点依次直线相连而成，这样形成的等高线在计算机和绘图仪上看起来不是一条光滑的曲线。为了获得光滑的等高线，还需要对等高线进行加密插补。

1 等高线跟踪

数字地面模型DEM是地形表面的计算机表示，DEM有多种表示形式，主要包括规则矩形格网与不规则三角网等。根据数字高程模型内插并排列等高线点的方法有很多，但总的来说可以大体分成2种：①按每条等高线走向顺序插点；②整体算求各等高线上的点并分别排列存贮［3］。第一种方法的基本思想是按逐条等高线的走向边搜索边插点，在搜索到等高线的起点后动态地依格网判断等高线走向，直到等高线回到起点或者穿出测区边界，它是通过判断等高线与格网或三角网边的交点来确定等高线的走向；后一种方法的基本思想则是先在整个DEM上搜索内插出全部等高线穿越格网边或三角网边交点的坐标，然后按照顺序依次将属于每条等高线的点找出来，并按等高线走向将这些点顺序排列并存储起来。

2 等高线平滑

通过相应的等高线跟踪算法，得到的是顺序排列的等高线点。提取出来的等高线将是一系列分段线性函数。这显然不符合实际地形的分布特征，因此，需要对它们作进一步的平滑处理。

等高线的平滑需满足下面几个要求：

1）曲线应通过已知的等高线点（常称为节点）；

2）曲线在节点处光滑，即其一阶导数（或二阶导数）是连续的；

3）相邻2个节点之间的曲线没有多余的摆动；

4）同一等高线自身不能相交［4］。

本文结合分段三次多项式与Akima法来对等高线进行平滑处理。

2．1 曲线拟合

2．1．1 分段三次多项式插值定义

分段三次多项式插值的含义是指在每2个数据点之间建立一个三次多项式曲线方程f（x），三次多项式方程表示为

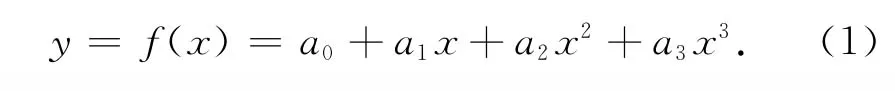
现在假设空间中存在依次用直线相连的n个离散点（xi，yi）（k＝1，2，…，n），x0＜x1＜…＜xn，在任意2个相邻的数据端点（xi，yi）和（xi＋1，yi＋1）之间拟合出一条三次多项式，且保证在端点处的一阶导数连续，即在端点处该三次多项的导数应该等于给定的值，这样就可以惟一确定三次多项式的各个系数。

根据上述条件可以惟一解得分段三次多项式的系数。分段三次多项式确定后可以按照一定的采样间隔在相邻两节点间进行加密插补。

2．1．2 空间离散点斜率的计算方法

在上一小节中进行求解分段三次多项式系数的时候要求节点函数的导数等于给定的已知值，这样才能保证整条曲线在各个节点处连续。Akima法是一种通过连续相邻5个空间离散点计算斜率的方法。假设空间中存在相邻的5个点，pk（xk，yk）（k＝i－2，i－1，i，i＋1，i＋2），Akima法以点Pi为端点的两弦斜率的加权平均值，Pi点斜率tanθi的计算公式为

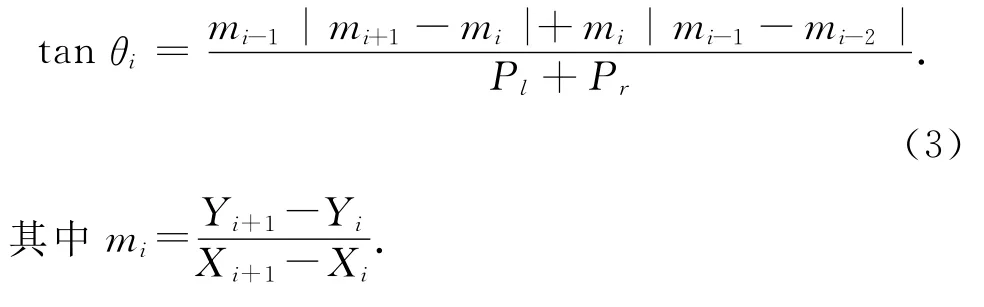
Pl和Pr即为Pi点左弦和右弦的权，它们分别等于Pi点前两弦斜率差的绝对值与后两弦斜率差的绝对值。即计算方法为

本文中的实验采用式（6）计算分母为零时的斜率。

2．1．3 端点处的补点

Akima法计算空间点的斜率分别需要左右相邻的各2个点，总共5个点，这样在等高线的起点处和终点处无法计算斜率，需要进行补点。对于闭曲线，补点的方法很简单，只需要将闭曲线的首尾相连，这样所有等高线点就是一个闭合的链表，如在计算起始点的斜率时，将闭曲线尾部2个点加进来即可。对于开曲线，补点通常可以按照下面的原则进行。

通过该方法求得补点的m值后，便可以通过式（3）计算端点处的斜率。

2．2 等高线的加密内插

2．2．1 基本方法介绍

通过上述曲线拟合的方法得到的是一系列的等高线方程，但是它们是解析函数，并不能通过计算机来显示。因此需要对曲线进行加密内插处理。

等高线内插的一个重要特征是：二维坐标系中，一个X坐标可能对应几个Y值。所以不能直接按照y＝f（x）的函数直接内插，应该采用曲线方程的参数形式分别对X和Y进行内插。任意平面曲线可以表示成参数为T的函数。

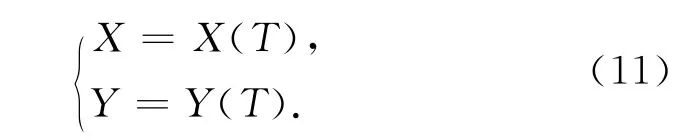
如图1所示，为将平面曲线表示为2个参数为T的参数方程，表示为参数方程后对应于定义域每一个横坐标值只会有一个X和Y值，这样就可以分别对X和Y值进行加密内插。

图1 平面曲线的参数方程表示

这里以对X为例来说明如何根据参数方程进行加密插补，对2个相邻等高线点（Xi，Yi），（Xi＋1，Yi＋1）的X拟合一个三次多项式曲线，即

其参数为T，这时参数T表示空间离散点间的折线长度。 设 空 间 中 存 在 6 个 空 间 点 （Xi－2，Yi－2），（Xi－1，Yi－1），（Xi，Yi），（Xi＋1，Yi＋1），（Xi＋2，Yi＋2），（Xi＋3，Yi＋3），它们距离点（Xi，Yi）的折线距离依次为S－2，S－1，S1，S2，S3。令（Xi，Yi）对应的 T 值为0，则X的曲线方程如图2所示，

图2 X关于T的参数曲线

等高线在节点处的斜率由Akima方法计算得到，令在（0，Xi），（S1，Xi＋1）处由 Akima法得到的斜率分别为tanθi和tanθi＋1，根据导数在节点处是连续的要求，可以得到

解得相邻等高线点（Xi，Yi），（Xi＋1，Yi＋1）的关于X参数方程的三次多项式后，以一定的步长ΔT对X值进行加密补点。以同样的方法依次对相邻等高线点间的X进行三次多项式拟合后加密插补，最后实现对整条等高线X的加密插补。对Y的加密插补方法同对X 的一样。X和Y都得到加密后就实现了对等高线的平滑。

2．2．2 插值步长ΔT的选择

插值步长ΔT如果选择得太小会使数据点大量重复造成数据冗余，如果选择得太大又达不到较好的平滑效果。对此，通过如下方法来对区间［Ti，Ti＋1］插值步长ΔT进行确定。曲线的最大逼近误差由式（18）估算。

对于等高线的参数方程平滑方法，可以用式（１９）分别求出X和Y的ΔTX和ΔTY，取其较小值作为最终的插值步长，d Smax取决于图形输出设备的精度。

3 实验与分析

对某一地区的DEM进行等高线跟踪进行等高线的自动绘制，得到该地区的自动绘制的等高线全局图如图3所示。

图3 自动绘制的等高线全局图

图4是该测区内某局部区域平滑前的等高线，图5是采用本文方法进行平滑后的等高线，实验中设定d Smax＝0．02来确定采样间隔。可以看出，平滑后的等高线看上去光滑连续，具有很好的视觉效果，并且更加接近作业员手工绘制的效果。

4 结束语

各种实验证明，利用本文提出的结合分段三次多项式与Akima法的等高线平滑方法，绘制出的等高线，很接近由训练有素的绘图员人工作业手工绘制的等高线，且方法稳定，效率高，对提高测绘产品的生产质量和生产效率具有十分重要的意义。另外，它不仅适用于绘制地形等高线，同样也可以用来绘制其他等值线图，具有极其广泛的应用前景。

［1］赵建三．基于格网DEM的自适应等高线内插方法［J］．中南工业大学学报：自然科学版，2003，2011（3）：315－319．

［2］荆玉英．地形图等高线的测绘方法［J］．测绘与空间地理信息，2008（5）：212－213．

［3］李德仁，王树根，周月琴．摄影测量与遥感概论［M］．北京：测绘出版社，2008．

［4］张剑清，潘励，王树根．摄影测量学［M］．武汉：武汉大学出版社，2003．

［3］聂桂根，万剑华．Akima插值法在测量中的应用［J］．测绘科技动态，1998（3）：31－34．

［4］邵才瑞．井筒数据的Akima插值重采样方法［J］．测井技术，2004（2）：112－114，179．

［5］唐彦，梁欣．分段三次多项式插值的节点导数研究［J］．黑龙江工程学院学报：自然科学版，2008，22（3）：78－80．

［6］聂欣，李鑫慧，吴良林．基于DEM生成等高线的方法［J］．地理空间信息，2009，7（4）：85－87．

［7］Wilson J P，Gallant J C．Terrain analysis：Principles and applications［M］．UK：John＆Wily＆Sons，2000．

［8］Wood J D，Fisher P F．Assessing interpolation accuracy in elevation models［J］．IEEE Computer Graphics and Applications，1993，13（2）：48－56．

Contour line smooth combined with segmental cubic polynomials with Akima

ZHENG Feng－jiao
（Wuhan Urban Design Survey Research Institute，Wuhan 430022，China）

The actual terrain generally changes continuously．Contour line automatically drawn through Digital Elevation Model（DEM）is formed by connected line segments，and it needs further smooth in order to describe actual terrain distribution more accurately．The paper combines segmental cubic polynomials with Akima method to smooth contour line．The experiment proves that the method has high efficiency and a satisfactory result，and achieves good smoothing effect．

contour line smooth；segmental cubic polynomials；Akima

P208

A

1006－7949（2012）03－0009－04

2011－05－20

精密工程与工业测量国家测绘局重点实验室开放基金资助项目（PF2009－22）

郑凤娇（1968－），女，高级工程师．

［责任编辑张德福］