齐次微分方程的解的存在性

黄晓芬，杨立兵

(1.海南师范大学数学与统计学院，海南海口571158 2.海南师范大学附属中学，海南海口571126)

0 引言

如果一阶微分方程

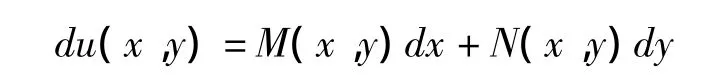
u(x，y)=c(c是任意常数).

定义如果二元可微函数 μ=μ(x，y)，使得 μ(x，y)M(x，y)dx+μ(x，y)N(x，y)dy=0 是一个全微分方程，则称 μ =μ(x，y)是方程 M(x，y)dx+N(x，y)dy=0 的一个积分因子.

对于一阶的常微分方程，如果它是全微分方程，可以用凑微分法，线积分法［1］等方法来求解出u=u(x，y)，从而得到通解.若它不是全微分方程，我们可以试图通过寻找积分因子［4，5］，使得这个方程是一个全微分方程，从而求出通解，比如，一阶的线性方程［2］，变量分离方程［1］，伯努利方程［3］均可通过积分因子求解.

1 相关引理和结论

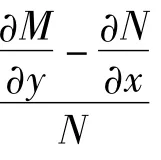
则有

由于M(x，y)和N(x，y)是齐次的，不妨设它们是m次的齐次的多项式，

则有

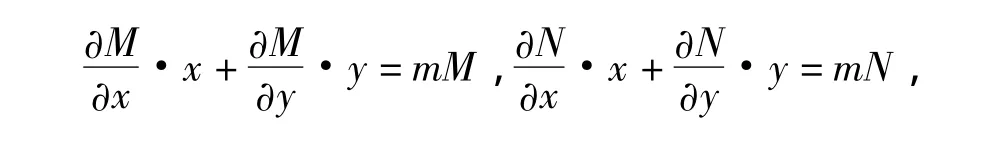
由上面的两个式子可推出

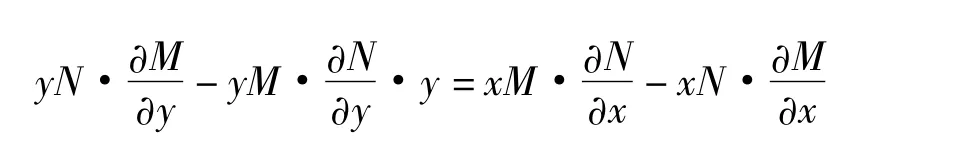
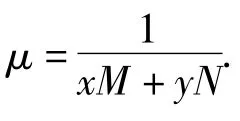
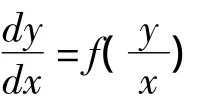
2 应用举例

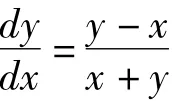
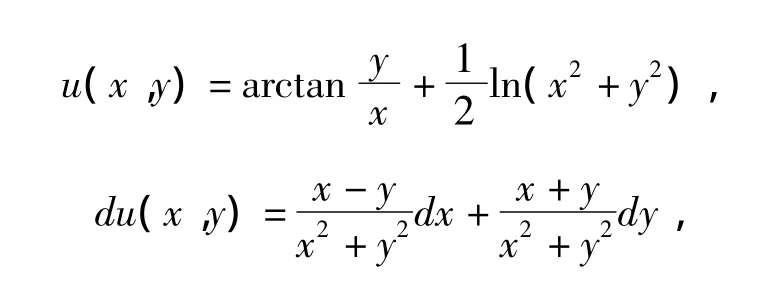
致谢作者感谢海南省自然科学基金111006和海南省自然科学基金610221的支持!

［1］王高雄，周之铭，朱恩铭，王寿松.常微分方程(第三版)［M］.北京.高等教育出版社，2006.

［2］陈伟.解一阶线性常微分方程的积分因子法［J］.高等数学研究，2008，11(3):27－28.

［3］胡劲松，郑克龙.用“积分因子”法求解Berloulli方程［J］.四川理工学院学报，2005，18(3):86－87.

［4］姚红梅.新复合型积分因子的存在定理及应用［J］.科学技术与工程，2010，10(15):3673－3674.

［5］屈芝莲.新积分因子的存在定理及应用［J］.科学技术与工程，2011，11(2):302－303.