相变材料热控系统内部接触热阻的辨识方法研究

石友安，桂业伟，杜雁霞，曾 磊，钱炜祺

（中国空气动力研究与发展中心，四川 绵阳 621000）

0 引 言

两种相互接触的固体材料的交界面，由于表面粗糙度的存在，微观上会呈现出“非一致接触”。当热流从一种材料经过界面向另一种传递时，由于“非一致接触”的存在，传热方式将发生变化：导热部分的热流将向接触点处收缩，空穴内的气体会带来对流传热，高温情况下，非接触的壁面还会发生辐射换热。这些变化都将对热量的传递形成一种阻碍作用，表现为界面附近的温度分布明显的降低，如图1所示。表征界面因非一致接触而产生的阻碍热流传递作用的物理量称为接触热阻［1］，数学定义式为：Rc＝ΔT／q。

相变材料热控系统是航天器及空间飞行器常用的一种热控系统。在封装过程中，由于材料凝固时的体积变化将导致相变材料与容器壁面之间形成非一致接触，从而产生接触热阻。对于高温条件下的热控系统而言，接触热阻的存在，在一定程度上降低了传热效率，容易产生局部高温，引发局部热应力，甚至带来局部破坏［2］。接触热阻已逐渐成为高温条件下热量精确控制的一项瓶颈因素。图2显示了在不考虑接触热阻情况下，以正二十八烷为相变材料的热控装置的计算与实验吸热融化过程相界面运动速度的比较。

图1 微观视角下的界面传热方式Fig.1 Heat transfer in interface between solids in microscopic view

由于接触界面处传热机理复杂、影响因素众多，譬如接触压力、界面温度等，且相变材料与容器之间的接触热阻又与材料凝固过程晶体的形成和生长特性密切相关，现有的理论计算方法大多过于简化，无法直接应用于工程实际。因此，采用反演热传导反问题的方法，将参数辨识中的灵敏度法和共轭梯度法应用到实验，建立了一种可用于稳态和瞬态接触热阻评估的辨识方法。通过模拟辨识和初步应用，得到了一些有意义的结论。

图2 在不考虑接触情况下，正二十八烷的计算与实验相界面移动特性比较Fig.2 Comparison of phase interface of C28H58between computation and experiment without consideration of thermal contact resistance（Rc）

1 计算模型

考虑接触热阻时材料融化的计算模型如图3所示。此时，材料内部的传热过程分为熔化前的导热过程和熔化开始后的固／液相变过程。

将传热简化为一维问题，则控制方程如下：

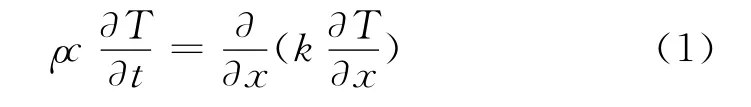
不考虑接触热阻时，边界条件为第一类边界条件：

初值条件：t＝1，T＝T0；

考虑接触热阻时：

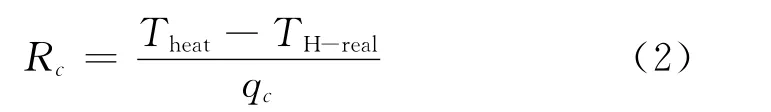
此时，固体内部的传热仍然满足一维传热方程，即式（1），但是，边界条件不同：

初值条件：t＝0，T＝T0；

综上所述，当存在接触热阻时，内部传热机制不变，但是边界条件等效为从第一类转变为第三类。

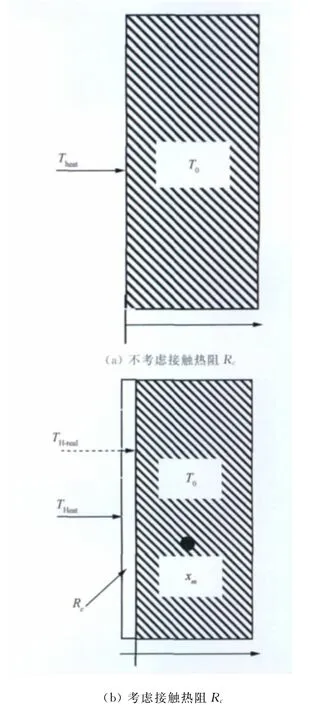
图3 热控装置内接触热阻的计算模型Fig.3 Calculation model of Rcin heat control equipment

2 参数辨识方法

辨识求解的思路是：以接触点测量温度Tm的时间历程为依据，在数值求解热传导正问题的基础上，根据输出误差原则，将反问题转化为一个优化问题来处理，等价于在函数空间中寻求合适的函数Rc或Rc（t）或Rc（xm，t），使如下目标泛函达到极小的过程：

式中符号意义：测点的坐标xm；测量温度Tm；计算温度T；测量误差ε。

2.1 稳态接触热阻的辨识

采用灵敏度法进行稳态接触热阻［3］的辨识，其优化策略是牛顿 拉夫逊（Newton－Raphson）算法［4］。下面介绍算法：

首先根据输出误差原则建立目标泛函：

优化算法描述如下：

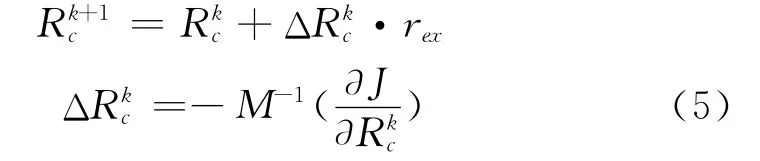
式中，参数的上标k，k＋1分别表示迭代前、后的参数值，rex是松弛因子。式中∂T／∂Rc为灵敏度，可以通过求解灵敏度方程得出。将式（1）对参数求导后即得到灵敏度方程。具体形式为（U定义为∂T／∂Rc）：

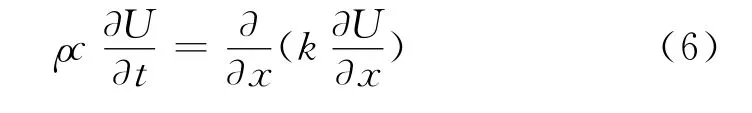
初值条件：t＝0，U＝0；

至此，稳态接触热阻辨识基本建立，依据式（5）进行辨识即可得到Rc。

2.2 瞬态接触热阻的辨识

相较于稳态而言，瞬态接触热阻［5］更能细致地刻画接触热阻的变化关系。采用共轭梯度法［6－7］进行辨识。算法描述：

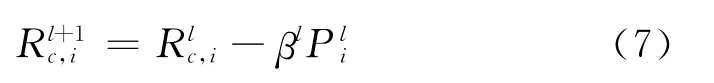
式中下标i表示接触热阻的时间离散次数；上标l、l＋1表示迭代层次，β为步长，P为共轭梯度，具体优化过程表述如下：

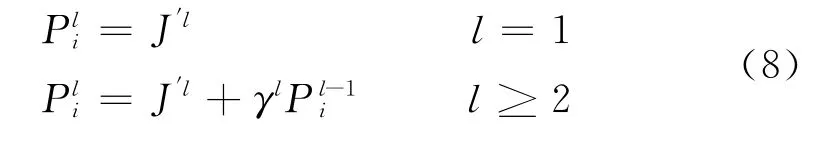
式中：J′l＝ （∂J／∂Rc，i）l

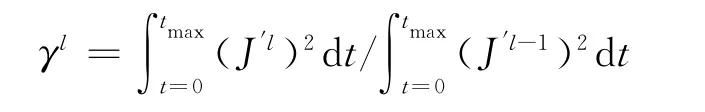
J′l－1和J′l是第l－1步和l步迭代的梯度下降方向，可以采用灵敏度分析或求解伴随方程来获取。由于满足目标泛函的温度场T，也必须满足主控方程，因此可根据拉格朗日乘数原理对目标函数进行扩展，得到如下扩展泛函：

式中λ为伴随变量。对上式后半部分积分再做变分，得到伴随方程：

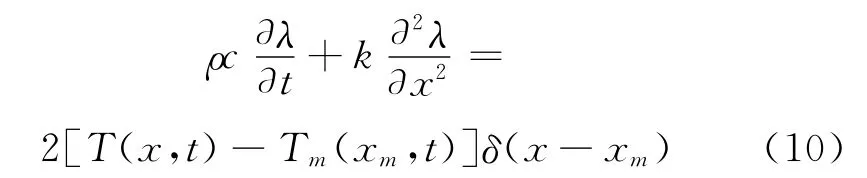
初值条件：t＝tmax，λ（x，tmax）＝0

边值条件：λ（0，t）｜x＝0＝0；

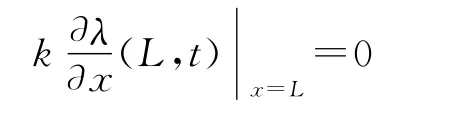
式中δ为克罗内克符号。整理得到，目标函数对Rc（T）的梯度为：

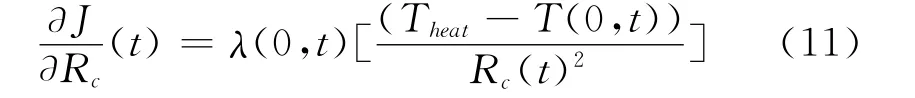
步长由下式计算：

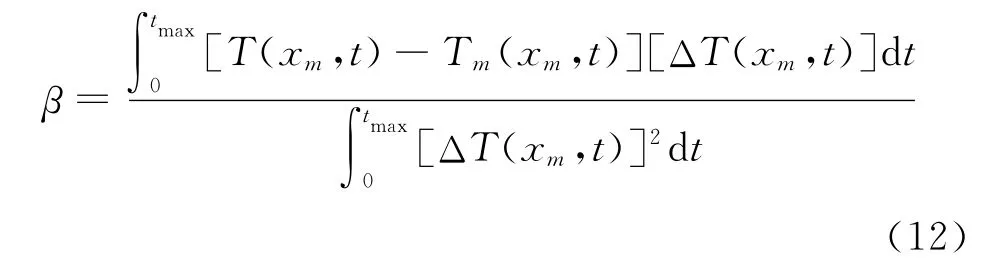
式中ΔT是由ΔR＝λn引起的温度场的变化值，可通过解灵敏度方程获得。

在优化过程中，收敛准则根据输出误差原则获得，即：

σ为测量误差的均方差，M为测点数。

至此，共轭梯度法已完全建立，依据式（7）进行辨识即可得到Rc（t）。

3 辨识方法的初步应用

采用封装二十八烷长方体热控单元进行融化实验，实验系统见图4，测点位置为x＝0.006m，y＝0.040m。采用电加热器作为恒温热源，温度控制采用ANV TF100PID自动演算控制器，通过加热功率的调节实现实验过程所需的加热边界条件，温度控制精度为±1K。温度信号由Agilent 34970A多点数据采集器采集。

图4 实验系统图Fig.4 Scheme of experiment system

实验测量温度数据见图5，从图中可以看出，温升斜率的增长趋势是先增加后减小，由此可以判定加热边界在测量记录中已经出现了融化。因此，辨识数据选取在0～300s内边界未融化的一段时间。

图5 测点温度数据Fig.5 Data of temperature at measured point

根据测点的温升历程测量参数进行辨识。分别取测量时间为100、140s进行稳态接触热阻的辨识，得到的结果依次为0.0799和0.0665。图6是利用稳态辨识值计算得到的测点温度与实测值的对比。可以发现：采用稳态辨识结果的计算温度值与实测值存在一定的差异，且随着时间的增长，差异增大，分析认为随着相变材料温度的升高，接触热阻可能随时间发生了变化，稳态接触热阻的假设可能带来了原理性误差。

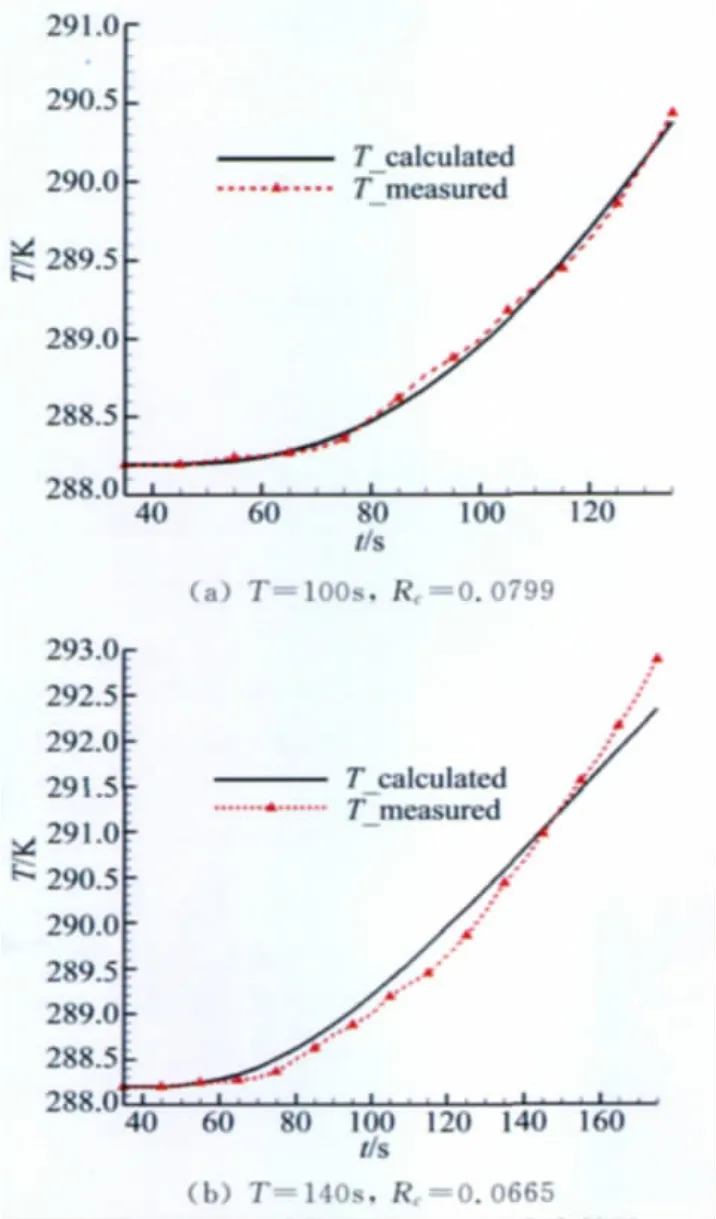
图6 测量温度和计算温度的对比（稳态结果）Fig.6 Comparison of temperature between calculation and experiment in steady Rc

为了提高界面接触热阻的辨识精度，进一步开展了瞬态接触的辨识。图7是瞬态接触热阻的辨识值。图8是测点的实测温度和计算温度的对比。可以发现：利用瞬态辨识值得到的测点计算温度能够更好的吻合实测温度。分析表明，随着加热时间的延长，材料温度不断升高，壁面和材料之间的空穴对热流的阻碍作用将减小，当材料出现融化后，融化的液体将填充空穴，接触热阻将继续减小，直至湮灭。这进一步证明了进行瞬态接触热阻辨识的可行性和可信性。

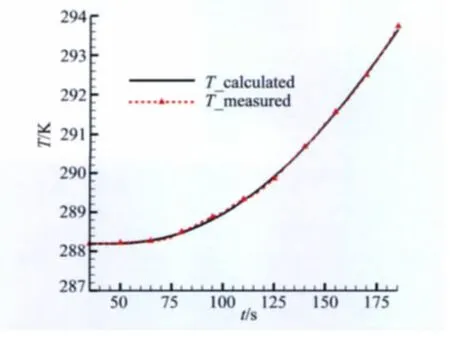
图8 测量温度和计算温度的对比（瞬态接触热阻）Fig.8 Comparison of temperature between calculation and experiment in unsteady Re

另外，对影响辨识质量的因素做了初步分析，发现：测温数据的信噪比是一个影响辨识质量的重要因素。测温数据是反问题求解的基础，其信噪比的高低直接决定求解过程能否克服非稳态传热固有的扩散性，影响解的稳定性，可参阅文献［6－8］。保障测量数据具有较高信噪比的措施之一是合理地安排测点的位置。图8是不同测点处的计算灵敏度的对比。从图中可以得到：越靠近加热边界，灵敏度越高。即在实验允许的情况下，测点位置宜尽可能地靠近扰动边界，以获得较高信噪比的测温数据。

图9 测点与边界处的灵敏度的比较Fig.9 Comparison of sensitivity between points in boundary and points in interior

为进一步研究接触热阻对材料熔化的延迟作用，初步应用稳态接触热阻辨识值，对75℃等温加热条件下，考虑和不考虑接触热阻效应的材料融化计算速率与相同条件下实验熔化速率进行了比较，如图9所示。当计及稳态接触热阻时，实验与计算熔化速率之间的吻合度有所提高，如图10所示。特别是融化延迟段很好地吻合试验，说明考虑界面接触热阻有利于提高熔化时间的预测准度。

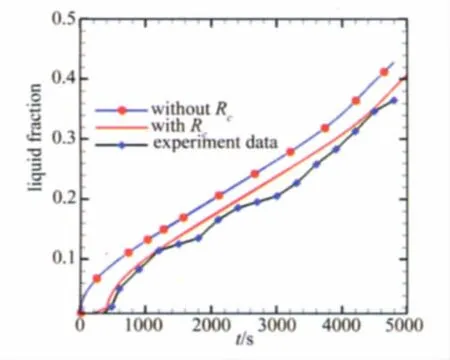
图10 稳态接触热阻对熔化速率的影响Fig.10 Influence of melt rate with consideration of steady Rc

4 小 结

将参数辨识方法引入相变过程界面接触热阻的辨识中，将数值计算与实验相结合，通过参数辨识获得了界面接触热阻的定量参数，对有效评估界面热阻对相变传热的影响作用提供了一种新的思路，得到了一些有意义的结果：

（1）所建立的稳态和瞬态接触热阻的两种辨识算法具有较高的精度、稳定性好、抗噪性强，算法有效；

（2）由于界面热阻的获得具有较大难度，采用基于传热反问题的参数辨识方法，是获得相变材料与容器之间界面热阻的一种有效途径。该方法对于获取复合相变材料等不易直接测量的物性参数也具有一定的参考价值；

（3）虽然初步应用验证了辨识算法的可行性，但是，由于接触热阻值较小，影响辨识质量的因素较多，且相变传热实验中还存在一些不确定因素，例如物性随温度变化。因此将辨识算法应用于实际工程，还需开展进一步的深入研究。

［1］ MADHUSUDANA C V，FLETCHER L S.Contact heat transfer－the last decade［J］.AIAA Journal，1986，24（3）：510－523.

［2］ WEI D，SUN X S，ZHU J M，et al.Structural response and behavior analysis of steel joint components at elevated temperatures［M］.Key Engineering Materials.2007，353－358：2672－2675.

［3］ JENNIFER Gill，EDUARDO Divo，ALAIN J Kassab.Estimating thermal contact resistance using sensitivity analysis and regularization［J］.Engineering Analysis with Boundary Elements，2009，33：54－62.

［4］ 钱炜祺，蔡金狮.再入航天飞机表面热流密度辨识［J］.宇航学报，2000，21（4）：1－6.

［5］ FIEBERG C，KNEER R.Determination of thermal contact resistance from transient temperature measurements［J］.International Journal of Heat and Mass Transfer，2008，51：1017－1023.

［6］ 石友安，曾磊，钱炜祺，等.热参数辨识在测热试验中的应用研究［J］.工程热物理学报，2010，31（9）：1555－1558.

［7］ OLIVEIRAY A P D，ORLANDE H R B.Estimation of the heat flux at the surface of ablating materials by using temperature and surface position measurements［J］.Inverse Problems in Science and Engineering，2004，20（5）：563－577.

［8］ BECK J V，BLACKWELL B，CLAIR C R S.Inverse heat conduction ill－posed problems［M］.New York：John Wiley ＆Sons，1985.