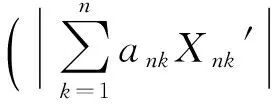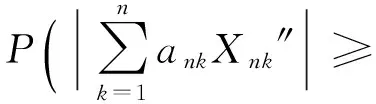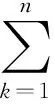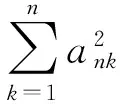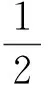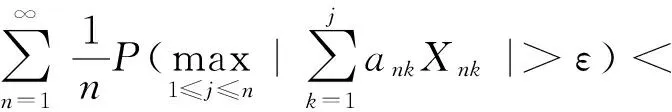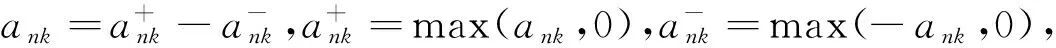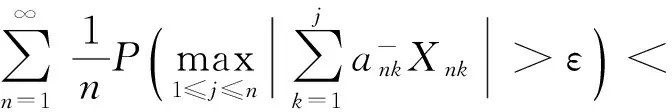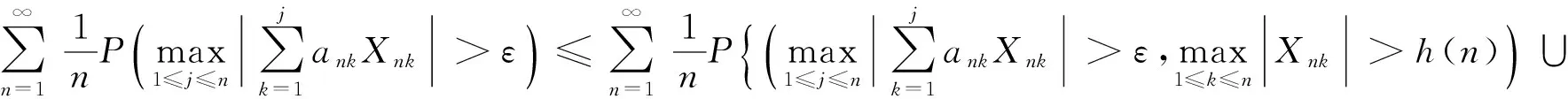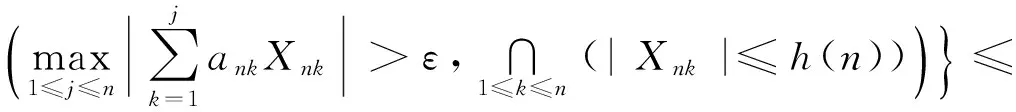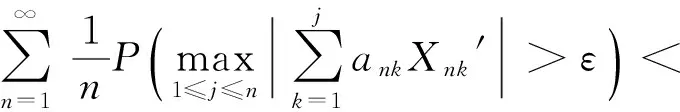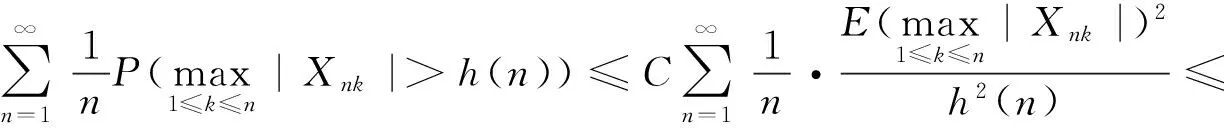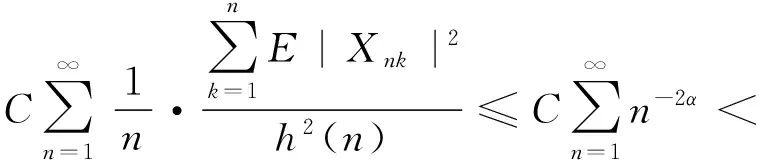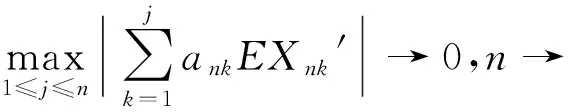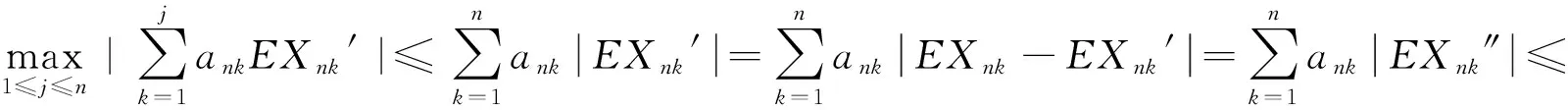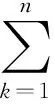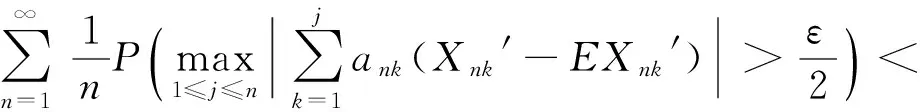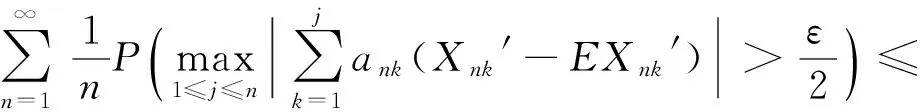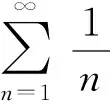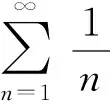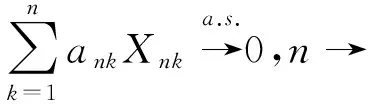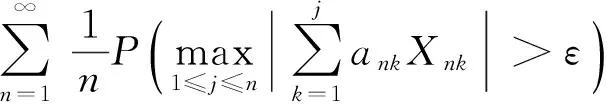两两NQD随机阵列加权和的弱大数定律和完全收敛性
伊艳娟,王文胜,赵丽媛
(杭州师范大学理学院,浙江 杭州 310036)
两两NQD随机阵列加权和的弱大数定律和完全收敛性
伊艳娟,王文胜,赵丽媛
(杭州师范大学理学院,浙江 杭州 310036)
利用截尾和矩不等式方法研究了在剩余h-可积条件下,两两NQD随机阵列加权和的弱大数定律和完全收敛性,得到两个重要的定理,推广和改进了已有的相应结果.
剩余h-可积;弱大数定律;完全收敛性;两两NQD阵列;加权和
1 背景及预备知识
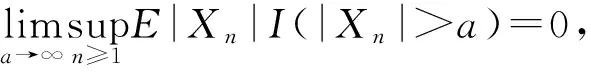
Lehmann[7]在1966年提出了两两NQD的概念.两两NQD列是包含两两独立和NA序列在内的非常广泛的概念,其中NA列在多元统计分析、渗透模型和可靠性理论中有广泛应用.因此,研究两两NQD列显得更为基本,更为重要.到目前为止,已有一些文献讨论了两两NQD列不同条件下的大数定律和完全收敛性定理,其中包括王和苏[8]讨论的同分布两两NQD列的弱大数定律,以及在混合条件下Marcinkixicz-Zygmund强大数定律和完全收敛性定理.吴[9]讨论了Kolmogorov-Chung型强大数定律并去掉了文献[8]中的混合条件,获得了与独立一致的完全收敛性定理.万[10]研究了两两NQD列在类似Cesàro可积的条件下,获得了与独立情形一样的弱大数定律和完全收敛性定理.Baek等[11]讨论了h-可积条件下两两NQD随机阵列加权和的完全收敛性.接着,章[12]讨论了h-可积条件下两两NQD随机阵列加权和带有缓变函数的完全收敛性定理.
剩余h-可积性比h-可积性更弱,也就是说,若一个随机变量序列是h-可积的,则一定是剩余h-可积,反之,不一定成立.但到目前为止,对剩余h-可积的研究仍然很少.本文主要研究了在剩余h-可积条件下,两两NQD随机阵列加权和的弱大数定律及完全收敛性,并且推广和改进了文献[11]的结果,将h-可积条件下的结果推广到了剩余h-可积条件下.
定义1[13]一个随机变量序列{Xn,n≥1}被称为是完全收敛到常数a,如果对任何ε>0,有
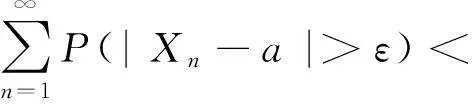
在这种情况下,我们称Xn完全收敛到a.
定义2[7]称随机变量X和Y是NQD(Negatively Quadrant Dependent)的,若对任意x,y∈R,有P(X 定义3[6]{ank}为常数阵列,称随机变量阵列{Xnk,un≤k≤vn,n≥1}是关于{ank}剩余h-可积的,若其满足: (1) 和 (2) (3) 和 (4) 引理1[9]设随机变量X与Y是NQD的,则 1)EXY≤EXEY. 2)对任意的x,y∈R,都有P(X 3)如果f,g同为非降(或非增)函数,则f(X)与g(Y)仍为NQD的. 则有 定理1设{Xnk,1≤k≤n,n≥1}为方差有限的行两两NQD随机阵列,{ank,1≤k≤n,n≥1}是常数阵列,{h(n),n≥1}是单调不减正常数序列,满足h(n)↑∞(n→∞).如果满足下列条件: (a){Xnk}是关于常数阵列{ank}剩余h-可积的; 证明记 Xnk′=XnkI(|Xnk|≤h(n))-h(n)I(Xnk<-h(n))+h(n)I(Xnk>h(n)), 则Xnk′,Xnk″均为Xnk的不降函数,由引理1知{Xnk′}和{Xnk″}也是NQD的.对任意给定的ε>0,有 由Markov不等式及Xnk′=min(Xnk,h(n)),有 (5) 最后一个不等式由定理条件(b)及剩余h-可积条件式(3)得到. (6) 最后一个不等式由剩余h-可积条件式(4)得到. 综合式(5)和式(6),定理1得证. 定理2设{Xnk,1≤k≤n,n≥1}为零均值且方差有限的行两两NQD随机阵列,{ank,1≤k≤n,n≥1}是常数阵列,{h(n),n≥1}是单调不减正常数序列,满足h(n)↑∞(n→∞).如果满足下列条件: (a){Xnk}是关于常数阵列{ank}剩余h-可积的; 那么,对所有的ε>0,有 (7) 和 因此,不失一般性,我们假设ank>0,Xnk′和Xnk″的记法如定理1.则由引理1可知{Xnk′}和{Xnk″}也是NQD的,令 要证式(7),只需证明: (8) 和 (9) 对于式(8),由Markov不等式及方差有限,有 (10) 为证式(9),先证 考虑到EXnk=0,再根据剩余h-可积的第二个条件式(2),可得 要证式(9),只需证 由Markov不等式,引理2及Xnk′=min(Xnk,h(n)),有 (11) 结合式(10)和(11),定理2得证. [1] Chandra T K. Uniform integrability in the Cesàro sense and the weak law of large numbers[J]. Sankhya Ser A,1989,51:309-317. [3] Chandra T K, Goswami A. Cesàroα-integrability and laws of large numbers, Ⅰ[J]. Theor Probab,2003,16:655-699. [4] Chandra T K, Goswami A. Cesàroα-integrability and laws of large numbers, Ⅱ[J]. Theor Probab,2006,19:789-816. [6] Yuan Demei, Tao Bao. Mean convergence theorems for weighted sums of arrays of residuallyh-integrable random variables concerning the weights under dependence assumptions[J]. Acta Appl Math,2008,103:221-234. [7] Lehmann E L. Some concepts of dependence[J]. Ann Math statist,1966,43:1137-1153. [8] 王岳宝,苏淳.关于两两NQD列的若干极限性质[J].应用数学学报,1998,21A(3):404-414. [9] 吴群英.两两NQD列的收敛性质[J].数学学报,2002,45(3):617-624. [10] 万成高.两两NQD列大数定律和完全收敛定理[J].应用数学学报,2005,28(2):253-261. [11] Baek J I, Ko M H, Kim T S. On the complete convergence for weighted sums of dependent random variables under condition of weighted integrability[J]. J Korean Math Soc,2008,45(4):1101-1111. [12] 章茜,王文胜.h-可积条件下两两NQD阵列加权和的完全收敛性[J].吉林大学学报:理学版,2010,48(2):183-188. [13] Hsu P L, Robbins H. Complete convergence and the law of large numbers[J]. Proc Nat Acad Sci,1947,33:25-31. WeakLawsofLargeNumbersandCompleteConvergenceforWeightedSumsofPairwiseNQDRandomVariable YI Yan-juan, WANG Wen-sheng, ZHAO Li-yuan (College of Science, Hangzhou Normal University, Hangzhou 310036, China) This paper discussed weak law of large numbers and complete convergence of the weighted sums of pairwise NQD random arrays under residualh-intergrability with the truncated and means moment inequality method, obtained two important theorems, which have extended and improved corresponding results. residualh-integrability; weak law of large numbers; complete convergence; pairwise NQD random arrays; weighted sums 2011-11-02 王文胜(1970—),男,教授,博士,主要从事概率极限理论及其应用研究.E-mail:wswang@stat.ecnu.edu.cn 11.3969/j.issn.1674-232X.2012.04.005 O211.4MSC201060F15 A 1674-232X(2012)04-0310-05
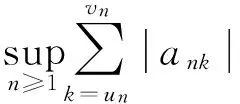
2 主要结论及证明
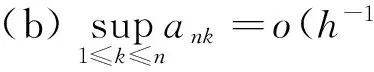
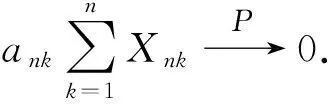
Xnk″=(Xnk+h(n))I(Xnk<-h(n))+(Xnk-h(n))I(Xnk>h(n)).