光子的质量与真空中光速的色散

阚学敏

(中国科学院广州地球化学研究所，广东广州 510640)

**本文把质量定义为不变量,不使用“静质量”这一术语.

光子的质量与真空中光速的色散

阚学敏*

(中国科学院广州地球化学研究所，广东广州 510640)

若光子是有质量的重光子，它的频率有一确定的最小值，光速则有一个确定的下限，仅低于极限速度c约10%.与介质中光速的色散不同，由光子质量引起的色散几乎全部集中发生在最小频率附近狭窄的频率范围内，高于长波无线电频率的电磁波的速度都是饱和的，即等于极限速度c.因此，“光速等于常数c”的测量结果以及康普顿散射实验，都不表明光子的质量必然为零.静电场的传播速度应该等于光速的下限，后者则是光速色散的标志，所以，测量静电场的传播速度等同于观察光速的色散，有助于判断光子是否有质量.

光子的最小频率； 光速的下限； 光速的饱和； 康普顿散射

经典的电磁场方程(麦克斯韦方程)隐含着光子质量为零的假设，电磁波的传播速度(即光速，指真空中，下同)是一个常数，色散为零.把光子视为有质量的粒子，即重光子，对麦克斯韦方程进行修正，可得到重电磁方程(Proca方程)[1-3]，这时光速与频率有关，应该有色散.但测量结果表明，光速等于常数c，没有色散，因此，“光子的质量等于零”已经写入了物理学的教科书.该结论存在可质疑之处，例如，对光速的精确测量都仅仅是在无线电超短波段和光学波段等较高频范围内完成的[4].在重光子假设下，作者在前文[5]指出，进入真空中传播的光子有一最小频率，光速则有一确定的下限值，本文讨论了由光子质量**引起的光速色散与光速饱和的过程.

光速的色散是光子有质量的证据，但是观测光速色散被认为是“前途渺茫的”[6], 本文则研究证明测量静电场的传播速度等同于观察光速的色散.

1 光速的色散

基于波粒二重性和能量的德布罗意关系式，可把光速表示为[5]:

(1)

其中mγ为光子的质量，常数c是速度极限[7]，ω为光子的频率，为普朗克常数.为了叙述的方便，本文不使用自然单位制，将在不同的地方分别使用mγ或两个不同的符号，并把后者

=

(2)

称为光子的静止频率[8]. 由重电磁理论导出的电磁波的群速度Vg[ 2-3，6 ]的表示式与(1)式相同.显然，随频率升高，c是光速的上限.

进入真空中的光子频率有最小值ωmin，它与有如下简单关系[5]：

(3)

因此，光速有一下限值[5]：

υmin=0.895c.

(4)

为弄清光速由υmin到c的色散过程,首先由式(1)求出光速的色散表示式:

(5)

光速υ的变化范围很小(0.895c≤υ≤c)，故光速的色散应近似地与频率的三次方成反比，因此，式(5)提示，光速的色散应该集中地发生在最小频率ωmin邻近的频率范围内.为了进一步讨论光速的色散过程，特别是要弄清光子质量对人们日常接触到的不同频率电磁波的速度产生的影响，必须给式(1)中的参数mγ设定一个合理的数值.

至今尚未观测到由光子质量引起的任何真实的物理效应(例如光速的色散)，当然不能够测定光子的质量.但是，已有一些实验方法[3,6]为光子的质量确定一个上限值，即光子质量的大小范围，其中当然也包括质量等于零.物理学文献中引用较多的是利用人造卫星，通过测量地球上空的磁场推算出来的光子质量范围：mγ≤4×10-48g[9], 以下的数值计算都以这一观测结果为根据.

取质量的最大值mγ=4×10-48g代入式(2)：

=0.543,

(6)

Smin[ωmin=2.24=1.22;υmin=0.895c]，

令ω1=10ωmin， 求出S1的坐标：

S1[ω1=10ωmin=12.2;υ1=0.999c].

图1 光速与频率的关系

由式(7)和(8)求出

(7)

所以，光速的变化(即色散)几乎全部(>99%)都集中发生在(ω1-ωmin=10.08)这一狭窄的频率范围内.以下将把(Smin→S1)之间的频率范围称为光速的色散带.

2 光速的饱和

随着频率的增高，在ω>>的条件下，可把光速的表示式(1)改写为

(8)

极限速度c与光速υ之差则可表示为

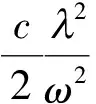
(9)

若令ω2=104(长波无线电频率)，就得到图1中S2的坐标:

S2[ω2=1×104;υ2=c-δ2]，

其中

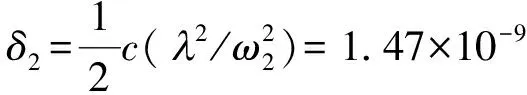
(10)

按照(9)式，常数c与光速υ之间的差值δ与频率的二次方成反比,所以式(10)中的δ2应该是图1中S2右侧2条曲线(虚线mγ=0和实线mγ=4×10-48g)之间，也就是常数c与光速υ之间速度差的最大值.若考虑到即使在光学频率下对光速测量的最好精度也仅达到±1米/秒[4](即±3.3×10-9c)，与式(10)相比,就不难理解,在S2的右侧 (ω≥ω2=1×104)，图中的2条曲线实际上是完全重合的，即光速是饱和的，因此，高频条件下，用实验方法未检测到光速的色散[3]，并不表明光子质量必然为零.

图1是按光子质量最大值(mγ=4×10-48g)得出的结果，不难说明，若保持图中(Smin→S1→S2…)曲线的形状不变，并把它的位置沿着与横坐标轴平行的方向，向左侧移动，直至趋近10-∞，则这些不同位置上的曲线就分别与0

3 康普顿散射与光子的质量

如果光子是有质量的粒子(mγ≠0 g)，mγ与能量E和动量p之间的关系应表示为

(11)

将能量E和动量p的表示式分别代入式(11)的左端，得到

E2-p2c2=(E2/c2)(c+υ)(c-υ).

(12)

在ω>>的情况下，将式(9)代入式(12)，同时取(c+υ)=2c，并与式(11)比较就得到

mγc2=E(/ω).

(13)

因此，在高频(ω>>)的条件下，式(11)右端的与左端2项中的任一项相比都是微小量，并随着频率增高而变得愈来愈微不足道，把它从式(11)中省略，即得到众所周知的光子的能量与动量间的简单关系:

E=Pc.

(14)

可以用康普顿散射实验更具体地说明式(11)与(14)之间区别的实质.将散射实验[8]使用的X-射线的频率ωx=4.2×1018代入式(13)，并应用式(6)，即可得到

mγc2=E(/ωx)=1.3×10-19E.

(15)

散射实验直接测量光子的能量E，所以式(15)表明，受实验误差的限制，mγc2的贡献本应忽略不计，可以用式(14)解释散射实验的结果[8].总之，式(14)只是在高频率下式(11)的精确近似结果，它并不表示光子的质量必然为零.

4 结论

与介质中电磁波的色散有着本质的不同，由光子质量引起的光速色散，几乎全部集中发生在频率最低端的狭窄的频率范围之内，使得高于长波无线电频率的光速都是饱和的(υ=c) ，光子的静能量mγc2与光子总能量E相比则微不足道，实际的测量不能对它有所觉察.因此，根据“光速等于常数c”或康普顿散射的实验结果，都不能判定光子是没有质量的粒子.“重光子”与“无质量光子”应是同样合理的假设.

光速的色散是光子质量引起的最重要的物理效应，但是，高于长波无线电频率时，光子质量引起的色散为零.在频率最低端，色散带(Smin→S1)的位置是不确定的，而且频率范围狭窄，所以，低频率下色散带的存在似乎也并不为观察光速的色散，即寻找光子的质量，带来便利或新的希望.

但是，和极限速度c相似，光速的下限值υmin=0.895c也是一个常数[5]，这是光子质量对光速造成的确定不变的影响，它与光子的质量大小无关(见式(1)和(3)).显然，测量光速的下限值，等同于观察光速的色散.

关于光子质量的讨论是从对静电场的研究开始的.在试图寻找光子质量的各种实验方法之中，研究静电场仍然被认为是最有希望的途径[6].假设光子的质量不为零，长久以来人们思考：库仑定律的平方反比是否严格正确[1，3，6]；现在认为问题应该是, 静电场的传播速度是否也等于极限速度c.测量静电场的传播速度，将有助于对光子有质量与否做出判断.

[1] JACKSON J D. Classical Electrodynamics[M]. New York: John-Wiley & Sons Inc, 1975: 5-9; 597-601.

[2] 蔡圣善, 朱耘, 徐建军. 电动力学[M]. 2版. 北京: 高等教育出版社, 2002: 404-407.

[3] 张元仲. 狭义相对论实验基础[M]. 北京: 科学出版社, 1979: 152-183.

[4] KAYE G W C, LABY T H. Tables of Physical and Chemical Constants and Some Mathematical Functions[M]. Fifteenth Edition. London and New York: Longman, 1986: 14-15.

[5] 阚学敏. 光子的质量与光速的下限[J]. 华南师范大学学报: 自然科学版, 2008(1): 67-70.

[6] GOLDHABER A S, NIETO M M. Terrestrial and extraterrestrial limits on the photon mass[J]. Revs Mod Phys, 1971, 43: 277-296.

[7] JACKSON J D. The impact of special relativity on theoretical physics[J]. Phys Today, 1987, 40: 34-42.

[8] 威切曼 E H. 量子物理学[M].复旦大学物理系，译. 北京: 科学出版社,1978: 188-204; 246-250.

[9] GOLDHABER A S, NIETO M M. New geomagnetic limit on the mass of the photon[J]. Phys Rev Letters, 1968, 21(8): 567-569.

[10] 阿希叶泽尔, 别列斯捷茨基. 量子电动力学[M].于敏,宋玉升,曹昌祺,等译. 北京:科学出版社,1964:313-318.

PhotonMassandDispersionoftheVelocityofLightinVacuum

KAN Xuemin*
(Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou 510640, China)

If a photon is massive, it will have a minimum frequency and the velocity of light will not be a constant but have a lower limit about 10% lower than constantc. Different from the dispersion of the velocity of light in medium, the dispersion in vacuum caused by the photon's mass concentrically appears within a narrow frequency region nearby minimum frequency and，so that, as the frequency is higher than that of long wave radio, the dispersion becomes zero and the velocity of light should be saturated (i. e. equals to constantc). In the result, “the velocity of light equals to constantc” of well known and Compton scattering should not necessarily mean that the photon is massless. It is tried to demonstrate that propagation velocity of the static field should be equal to the lower limit of the velocity of light, and the latter means that there is the dispersion. Therefore, experimental determination of the propagation velocity of static field equates with observation of dispersion and is helpful to answer whether the photon is massive or massless.

2011-12-21

*通讯作者,kanwang@gig.ac.cn.

1000-5463(2012)03-0071-04

O412.1；O413.2；O442

A

10.6054/j.jscnun.2012.06.016

Keywords： photon’s minimum frequency; lower limit of the velocity of light; saturation of the velocity of light; compton scattering

【责任编辑 成 文】