估计对流层延迟的单频RTK卡尔曼滤波算法

徐彦田，程鹏飞，蔡艳辉，甄 杰，徐宗秋

(1.辽宁工程技术大学测绘学院，辽宁阜新123000;2.中国测绘科学研究院，北京100830)

估计对流层延迟的单频RTK卡尔曼滤波算法

徐彦田1，程鹏飞2，蔡艳辉2，甄 杰2，徐宗秋1

(1.辽宁工程技术大学测绘学院，辽宁阜新123000;2.中国测绘科学研究院，北京100830)

提出一种对流层估计方法实现单频RTK快速动态定位。用模型改正对流层干延迟，双差对流层湿延迟用测站对流层天顶延迟估计，并与流动站位置及站间单差模糊度组成双差方程进行卡尔曼滤波，得到单差模糊度浮点解及方差阵，通过星间求差得到双差模糊度浮点解及方差阵，结合MLAMBDA方法实时确定模糊度。试验验证单历元平面定位精度优于±3 cm，高程定位精度优于±10 cm。

单频RTK;MLAMBDA;对流层天顶延迟(TZD);整周模糊度

一、引 言

GPS单频接收机只能捕获C码和L1载波相位观测值、多普测观测值及导航电文，其成本较低、结构简单，易与其他设备集成，因此，如何消除各种误差的影响，利用相对廉价的便于携带的单频接收机实现较大范围、高精度实时定位是目前卫星大地测量研究的热点和难点问题之一［1-2］。本文分析了对流层延迟的特点，将其分为干分量和湿分量，干分量的模型精度达到亚毫米级，而湿分量(约占10%)具有较强的时间性和空间性，其值达到10～40 cm，模型精度不能满足高精度定位，差分技术不能有效削弱其影响。因此，本文将双差对流层湿延迟用测站对流层天顶延迟进行一阶马尔可夫估计，并与流动站位置及站间单差模糊度组成双差方程进行卡尔曼滤波，得到单差模糊度浮点解及方差阵，通过星间求差得到双差模糊度浮点解及方差阵，结合MLAMBDA方法［3-7］逐历元搜索模糊度。试验验证单历元平面定位精度优于±3 cm，高程定位精度优于±10 cm。采用单差状态向量的马尔可夫过程避免了基星使用多次造成的相关性，但仍然保持了双差的特性，并且单差模糊观测值的权与高度角的关系更容易确定［8］。

二、双差对流层延迟估计

对流层延迟分为干分量和湿分量，干分量的模型精度达到亚毫米级，而湿分量(约占10%)具有较强的时间性和空间性，其值达到10～40 cm，模型精度不能满足高精度定位。为了估计湿分量的大小，采用一阶高斯马尔可夫过程估计测站对流层天顶湿分量，从而获取信号传播路径上双差对流层湿延迟，表示为

式中，Δ 为站星间双差;ε为高度角;i为非基准卫星;j为基准卫星;A、B为测站标示;Mf()采用适用于大于3°卫星的NMF投映函数，即

三、单频RTK卡尔曼滤波算法

1.单频RTK卡尔曼滤波模型

将测站A、B的对流层天顶延迟组成观测方程进行卡尔曼滤波估计，忽略轨道误差和多路径影响，采用站间单差模糊度，站星间双差观测方程的卡尔曼滤波方程可表示为

其中，Δ为站间单差;N为模糊度;ρ为站星间几何距离;λ为波长

2.第k历元滤波过程

第k历元单点定位［X Y Z］k预报状态向量的位置分量

基于k－1历元滤波误差方差阵Pk－1和单点定位方差阵P［XYZ］k以及处理噪声阵Qk计算k历元预测误差方差阵Pk，k－1

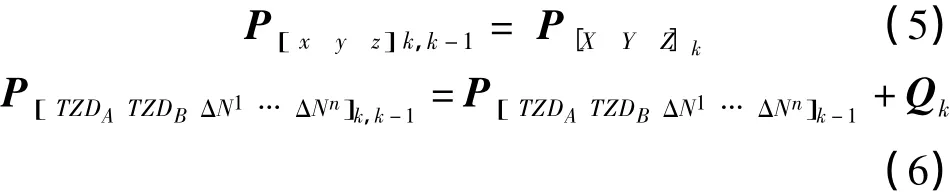
计算滤波增益阵Kk和改正数vk，修正第k历元预测值得到卡尔曼滤波解为

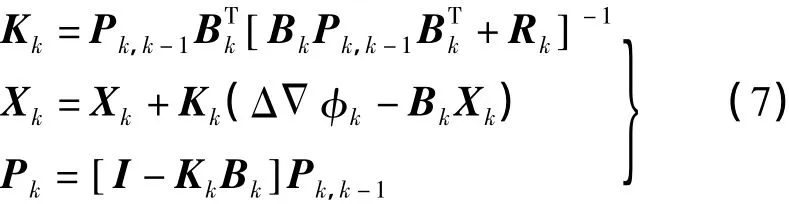
最终解算得到站间单差模糊度浮点解及其方差阵，利用星间求差得到站间星间双差模糊度浮点解及方差阵，结合MLAMBDA方法逐历元固定模糊度。

四、试验与分析

试验采用IGS网站提供的GUAM和GUUG站数据，基线长18.678 km，数据为2009年3月4日(GPS时)的1000个历元的观测数据(采样间隔为30 s，卫星截止高度角10°，总共解算模糊度17个，最多公共卫星数10颗。

由于站间基线距离较长，对流层延迟双差后不能完全消除，根据以上的算法得到天顶对流层延迟，图1显示单站延迟绝对值最大值超过10 cm，前后历元变化较小;两站延迟最大差值为8 cm，因此将天顶对流层延迟分解成两个状态参数滤波是有必要的。

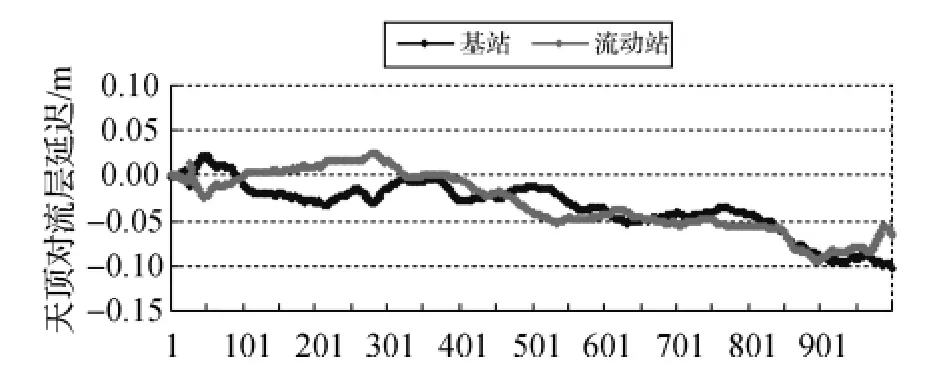
图1 TZD滤波值示意图

图2为观测时段较长的PRN15和PRN14卫星传播方向上双差对流层延迟。可以看出高度角较小时残差较大，PRN14最大值达7.6 cm，近L1波长的一半，给模糊度固定带来困难，而随着卫星高度角的增大，双差对流层延迟变小，卫星达到一定高度时可以忽略。

图2 双差大气延迟残差

图3显示滤波稳定后，双差模糊度浮点解和固定解差值一般在1周以内，模糊度易于固定，搜索效率较高，并且Ratio值(见图4)较大。由图3和图4可以看出，当可用卫星数频繁变化时，模糊度滤波值相应出现较大抖动，Ratio值瞬时变小频繁抖动，甚至出现固定失败;而增加新升卫星时，由于模糊度初值和方差阵误差较大，Ratio值急剧变小;对于稳定卫星数，Ratio值是递增的。

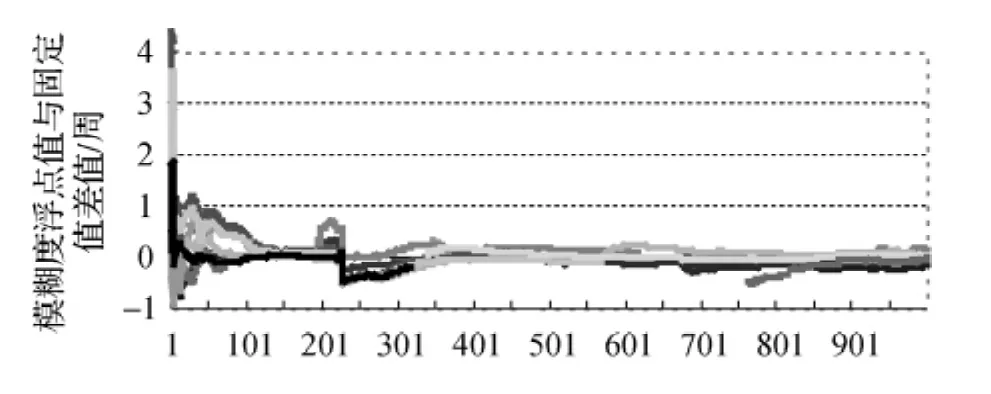
图3 17个模糊度滤波值偏差示意图

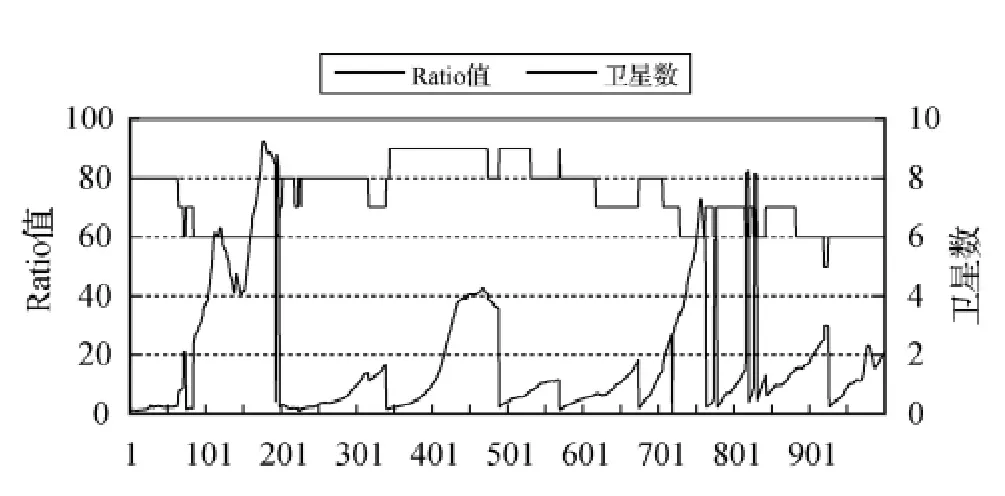
图4 Ratio值与可用卫星数

通过MLAMBDA方法固定载波相位双差模糊度后，改正流动站位置滤波值得到L1载波相位单历元定位值，图5显示卫星数平稳时固定解平面定位精度优于 ±3 cm以内，高程定位精度优于±10 cm，滤波稳定后浮点解定位平面精度保持在±6 cm，高程精度保持在±15 cm内。

图5 L1观测值单历元定位精度

五、结束语

经试验验证双差对流层延迟残差随着高度角增加逐渐减小，高度角大于一定阈值时可以忽略其影响，测站天顶对流层延迟最大差值超过8 cm。若将天顶对流层延迟作为一个状态参数进行滤波，投影到卫星路径会影响模糊度浮点解精度，可能导致模糊度固定失败，因此天顶对流层延迟分解成两个状态参数滤波是有必要的。滤波稳定后，双差模糊度浮点解和固定解差值一般在1周以内，模糊度易于固定，搜索效率高;18 km基线固定解平面定位精度优于±3 cm，高程精度优于±10 cm，实现了单频RTK快速动态定位，可满足实际需要。

［1］ CHENG Pengfei.Investigation on the Establishment of DGPS Services in China［D］.Austria:the Graz University of Technology，1998.

［2］ 程鹏飞，蔡艳辉，文汉江，等.全球卫星导航系统［M］.北京:测绘出版社，2009.

［3］ 刘志平，何秀凤，郭广礼.GNSS模糊度降相关算法及其评价指标研究［J］.武汉大学学报:信息科学版，2011，36(3):257-261.

［4］ TEUNISSEN P J G.The Least-Squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation［J］.Journal of Geodesy，1995，70:65-82.

［5］ CHANG W，YANG X，ZHOU T.MLAMBDA:A Modified LAMBDA Method for Integer Least-squares Estimation［J］.Journal of Geodesy，2005，79:552-565.

［6］ 周扬眉，刘经南，刘基余.回代解算的LAMBDA方法及其搜索空间［J］.测绘学报，2005，34(4):300-304.

［7］ TEUNISSEN P J G.A New Method for Fast Carrier Phase Ambiguity Estimation［C］∥Proceedings IEEE Position Locationand Navigation Symposium PLAN94. Las Vegas:［s.n.］，1994:562-573.

［8］ BENJAMIN W，REMONDI，GROVER B.Triple Differencing with Kalman Filtering:Making It Work［J］.GPS Solutions，2010(3):58-64.

A Kalman Filter Algorithm for Single-frequency RTK Solution

XU Yantian，CHENG Pengfei，CAI Yanhui，ZHEN Jie，XU Zongqin

0494-0911(2012)08-0004-03

P284

B

2011-11-03;

2012-03-02

中国测绘科学研究院基本科研业务费(7771017;7771202);地理空间信息工程国家测绘地理信息局重点实验室开放基金(201103)

徐彦田(1983—)，男，河北石家庄人，博士生，研究方向为GNSS数据处理。