图像中的噪声及其复原方法的比较研究

司 洋

（中北大学 信息探测与处理技术研究所，山西太原 030051）

0 引言

早在20世纪初，人类为了用图片及时传输世界各地发生的新闻事件，便开始了对图像处理技术的研究。用计算机进行图像处理，改善图像质量的有效应用开始于1964年，美国喷气推进实验室对太空传回的大批月球照片进行处理，并收到了明显的效果。然而，图像处理技术的真正发展还是在上世纪60年代末，其原因一方面是由于受到航天技术发展的刺激，另一方面是作为图像处理工具的数字计算机和各种不同类型的数字化仪器及显示器的突飞猛进发展。迄今为止，数字图像作为一门崭新的学科，日益受到人们的重视，并且在科学研究、工农业生产、军事技术和医疗卫生等领域发挥着越来越重要的作用。

但在获取和传输图像过程中，图像常常受到成像设备与外部环境噪声的干扰而降质，不可避免地要含有噪声。所以在处理和传输时，就必须对图像进行去噪处理，以提高图像的质量。图像去噪是图像处理的常用技术，经典的图像去噪方法从本质上来说，是低通滤波的方法，低通滤波器在有效消除噪声的同时，也会使图像的边缘信息模糊，从而使图像失真较大。近年来，小波理论得到了非常迅速的发展，由于其具有良好的时频特性，因而实际应用也非常广泛。在去噪领域中，小波理论也同样受到了许多学者的重视，他们应用小波进行去噪，并获得了非常好的效果。

1 去噪处理

1.1 中值滤波的原理和关键技术

中值滤波使用一个矩形区域的窗口sxy。不同的中值滤波过程, 中值滤波器的滤窗大小不同（本文采用滤窗大小为3×3）。同时当判断滤窗中心的像素是噪声时,该值用中值代替,否则不改变其当前像素值,这样用滤波器的输出来替代像素(x,y)处(即目前滤窗中心的坐标)的值。

先做如下定义：

Zmin是sxy滤窗内的灰度的最小值；

Zmax是sxy滤窗内的灰度的最大值；

Zmed是sxy滤窗内的灰度的中值；

Zxy是坐标(x,y)处的灰度值；

B1=Zxy-Zmin；

B2=Zxy-Zmax。

如果B1＞0并且B2＞0,把Zxy作为输出值，否则把Zmed作为输出值。

理解该算法的关键在于，要记住它有3个主要目的:除去“椒盐”噪声(冲激噪声)，平滑其他非冲激噪声，并减少诸如物体边界细化或粗化等失真。Zmin和Zmax的值进行统计后被算法认为是类冲激噪声成分，即使它们在图像中并不是最低和最高的可能像素值。检测窗口检测Zxy中心点本身是否是一个脉冲。若条件B1＞0且B2＜0为真，那么Zmin＜Zxy＜Zmax，Zxy就不是脉冲。在这种情况下，算法输出一个不变的像素值Zxy，通过不改变这些“中间水平”的点，来减少图像中的失真。如果条件B1＞0且B2＜0为假，则Zxy=Zmin或Zxy=Zmax。在任一种情况下像素值都是输出中值Zmed。

中值滤波程序流程图如图1所示。

图1 中值滤波程序流程图

1.1.1 实际运用中的关键技术

如果使用一个图像数据内存,在对某一个像素点进行滤波运算完成后，该像素点的灰度值有可能要被数组中的中值所代替，把运算结果保存在该像素点所在处,接着对下一个像素进行运算，那么前一个像素运算结果直接参与到下一个像素的滤波，运算中，这样导致大量的图像细节丢失。所以做法是申请图像大小的两个内存空间，把图像像素保存到两个内存中，对第一个内存进行滤波，运算后的结果保存到第二个内存中。

1.1.2 中值滤波具体实现代码

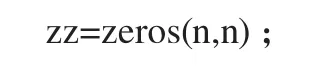
%得到3×3窗体内的最小值最大值，中间值

1.1.3 中值滤波降噪结果分析

本文利用大小为256×256的图像对中值滤波降噪算法进行了模拟仿真，仿真结果如图3所示。

图3 原始图像加噪及恢复

其中，原始图像，如图3(a)所示，加上白噪声后得到噪声图像，如图3(b)所示。图3(c)所示，是采用3×3的中值滤波器去噪后得到的图像，可以看出，还原后明显比图3(b)所示图像要好得多，没有突出的噪声点。

1.2 小波降噪的原理和关键技术

1.2.1 基于小波的噪声去除

在数学上，小波去噪问题的本质是一个函数逼近问题，即如何在由小波母函数伸缩和平移版本所展成的函数空间中，根据提出的衡量准则，寻找对原信号的最佳逼近，以完成原信号和噪声信号的区分。从信号学的角度看，小波去噪是一个信号滤波的问题，而且尽管在很大程度上小波去噪可以看成是低通滤波，但是由于在去噪后，还能成功地保留图像特征，所以在这一点上又优于传统的低通滤波器。由此可见，小波去噪实际上是特征提取和低通滤波功能的综合。

小波去噪方法大体可以分成小波萎缩法、投影方法、相关方法3类。小波萎缩法是目前研究最为厂泛的方法，它又可分成如下两类：第1类是阈值萎缩，由于阈值萎缩主要基于如下事实，即比较大的小波系数一般都是以实际信号为主，而比较小的系数则很大程度是噪声。因此可通过设定合适的阈值，首先将小于阈值的系数置零，而保留大于阈值的小波系数:然后通过阈值函数映射到估计系数:最后对估计系数进行逆变换，就可以实现去噪和重建。第2类方法称为比例压缩，即通过判断系数被噪声污染的程度，并为这种程度引入各种度量方法(例如概率和隶属度等)，进而确定萎缩的比例。

阈值的确定在阈值萎缩中是最关键的。目前使用的阈值可以分成全局阈值和局部适应阈值两类。1995年，Donoho首先提出了小波阈值的概念。目前提出的全局阈值主要是：

(1) Donoho和Johnstone统一阈值(简称DJ阈值)其中，σ为噪声标准方差，N为信号的尺寸或长度；

(2)基于零均值正态分布的置信区间阈值δ= 3σ～4σ；

(3) Bayesshrink阈值和MapShrink阈值；

(4)最小最大化阈值；

(5)理想阈值。

实验结果表明，在图像不是很大的时候，采用全局阈值就可以达到很好的效果。阈值函数主要分为硬阈值函数、软阈值函数以及半软阈值函数。其中硬阈值函数为δ(w) =wI(|w|＞T)，而软阈值函数为δ(w) = (w- s gn(w)T)I(|w| ＞T)，其中I为示性函数。总的来说，硬阈值函数可以很好地保留图像的边缘等局部特征，软阈值函数处理结果相对平滑得多，但是图像的边缘会出现失真现象。所以本文选择硬阈值函数。

1.2.2 小波降噪具体代码

%use sym4 3层小波分解

[c,s]=wavedec2(I,3,' sym4’)；

%门限

n=[1,2,3]；

p=[150,120,60]；

%阈值处理

nc=wthcoef2('d',c,s,n,p,'s')；

%recover图像重构

rx=waverec2(nc,s,'sym4')；1.2.3 小波降噪的实验结果分析

下面是本文利用大小为256×256的图像对小波阈值降噪算法进行了模拟仿真，仿真结果如图4所示。

其中，噪声图像是由原始图像加上白噪声后得到的，如图4（b）所示。图4（c）是用小波阈值降噪法还原后的图像,可以看出图像明显比图4（b）暗淡,这是因为它的高频被滤除了一部分,但是它的噪声明显减少了。

图4 原始图像加噪及恢复

2 实验结果分析

这里将前面的方法进行了对比（见图5），其中也将某些方法结合起来对加有混合型噪声的图像进行了去噪处理，并从这些方法的最终效果得出结论。

在进行去噪的过程中，普通的中值滤波器在抑制椒盐噪声的同时也能较好地保留图像的边缘信息，但它对高斯噪声的抑制能力却很小。而在采用小波阈值去噪方法对这种含综合性噪声的图像进行去噪时，其对高斯噪声有很好的抑制作用，但对椒盐噪声基本无效。所以，不同的方法有不同的效果，但是总的说来，小波阈值降噪的效果要好于中值滤波器。

图5 原始图像加噪及两种恢复方式

[1]张亶,陈刚.基于偏微分方程的图像处理[M].北京:高等教育出版社,2004:61-62.

[2]杨新主.图像偏微分方程的原理与应用[M].上海:上海交通大学出版社,2003.

[3]Rosenfeld Akaka A C. Digital Picture Processing[M].New York: Academic Press,1982.

[4]姚海根.图像处理[M].上海:上海科学技术出版社,2000.

[5]沈庭芝,方子文.数字图像处理及模式识别[M].北京：北京理工大学出版社,1998.

[6]胡昌华.MATLAB6.X的系统分析与设计—小波分析[M].西安:西安电子科技大学出版社,2007:5-15.

[7]徐建华.图像处理与分析[M].北京:科学出版社,2008.

[8]PrattWK.Digi Imlnage Processing[M].NewYOrk:ley,2009.