复合材料拉托力预测中标准差加权融合算法★

李 盼，杨风暴，王肖霞，樊庆英

（中北大学 信息与通信工程学院， 山西太原 030051）

0 引言

粘接作为联接材料或结构的手段有诸多的优越性，比如施工方便、联接应力分散、对粘接体本身要求低，适用面广等[1]。但是，由于粘接层间脱粘或粘接强度未达到设计要求或在使用过程中强度降低而引发的各种灾难性事故时有发生，如几乎所有的飞机和导弹中都包含粘接组件，粘接强度的好坏直接影响整体机构的运行。构件粘接中容易发生脱粘等问题，造成粘接强度降低。金属与非金属之间的粘接较同种材料之间的粘接更为困难，很容易出现脱粘，导致粘接强度降低。因此，对此类粘接强度的检测尤为重要。采用多传感器数据融合可预测出金属与非金属粘接材料的拉托力，可以给这种复合材料的粘接强度一个定量的描述。

多传感器数据融合技术具有以下优点：(l)提高了系统可靠性、可信度。由于多传感器相互配合，减少了系统内在的冗余度，降低了系统故障率。各个传感器的判断结果相互补充确认，增强融合后的可信度；(2)扩大了系统空间覆盖范围。通过多个交叠覆盖的传感器作用区域，一些传感器可以探测到其它传感器无法探测的地方；(3)减少了信息的模糊性。由于采用多传感器的信息进行检测、判断、推理等运算，降低了事件的不确定性；(4)改善了系统探测性能。利用多传感器信息，可以在虚警一定的情况下，提高系统的发现概率；(5)提高了系统定位精度。利用多传感器信息可以减小测量误差，提高测量精度。

1 数据融合基本原理

多传感器数据融合的基本原理就是充分利用多传感器资源，通过对这些传感器及观测信息的合理支配和使用，将各种传感器在空间或时间上的冗余或互补信息，依据某种准则组合起来，产生被测对象的一致性解释或描述[2]。其目的是基于各传感器分离的观测信息，通过对信息的优化组合导出更多的有用信息，最终目标是利用多传感器共同或联合的操作优势，来提高整个传感器系统的有效性，消除单个或少量传感器的局限性。

数据融合的基本目标是通过数据组合而不是出现在输入信息中的任何个别元素，推导出更多的信息，这是最佳协同作用的结果。多传感器数据融合系统通过有效的利用多传感器资源，最大限度地获得被测目标的信息[3]。

加权融合算法由于实现起来较为容易, 所以在工程实际中得到了广泛的运用。然而权值的分配对融合结果起到十分重要的影响。文献[4]给出了按矩阵加权线性最小方差融合估计公式, 文献[5]给出了按标量加权融合估计公式, 文献[6]给出了按对角阵加权融合估计。目前, 利用数据间的距离按矩阵加权融合是较为常见的一种方法[7]。此外贝叶斯估计和D-S证据推理方法也是常用的融合算法，但采用贝叶斯估计时，当未知前提的数目大于已知前提数目时，已知前提的概率分布变的不稳定；D-S证据推理方法使用了不稳定区间可以通过未知前提的先验概率解决贝叶斯估计的不足，比较适用于决策级融合，但在本文中并不是简单的二值分类，而是对粘接力的融合，则D-S证据推理方法也不能很好的解决。本文中为了准确预测金属与非金属粘接的拉托力，采用声阵列[8]方法来放置传感器，并使用基于标准差加权融合算法。该算法可在不知道传感器任何先验知识的情况下，利用标准差给各个传感器分配权值，得到多传感器融合估计数据，达到充分利用多传感器提供的信息，有效地利用各个传感器数据的目的。

2 声阵列传感器的加权融合估计算法

2.1 传感器的确定

在声阵列检测中，每个传感器在接受其所在位置的粘接信息时也检测到其它位置的信号，由于声波传输和叠加的复杂性，从一个传感器的信号中分析出位置信息很难。但是各个传感器之间的主要区别就是位置不同造成检测信号之间的差异。

以两个传感器为例，图1为传感器位置的确定。

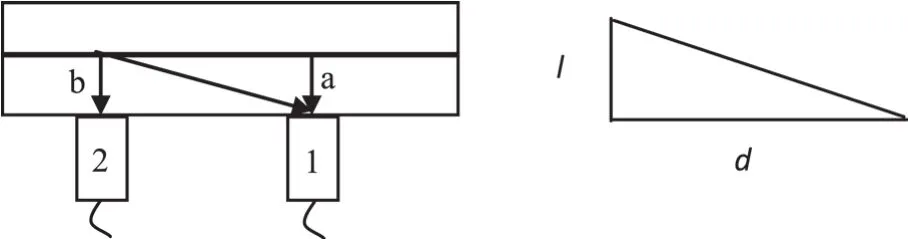
图1 传感器位置的确定

传感器1先接到其对应位置a的信号然后再接到位置a、b两处叠加在一起的信号。设声波在介质中的传播速度为v，介质的厚度l,传感器之间的距离为d，则可以计算出传感器只接受其对应位置粘接信号的时间t，如式（1）

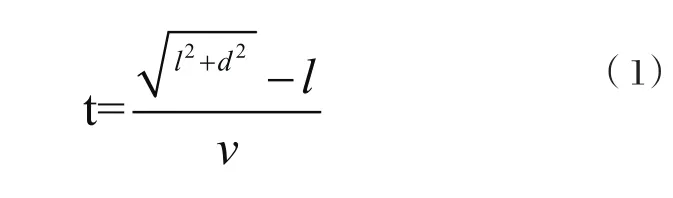
因此可以认为在时间t内检测的信号主要来自传感器本身对应的位置，式（1）中的d选取时要根据所选传感器检测的有效范围而定。而在实际实验时，由于每个传感器的检测有效范围受声波在介质中的衰减、传播路径、速度、介质几何尺寸等因素影响，从理论上计算比较困难，此种方法只是在实验中尽可能的减少传感器之间的冗余信息。

2.2 融合算法

选取M个传感器根据式1放置。做N次实验，则得到的传感器数据

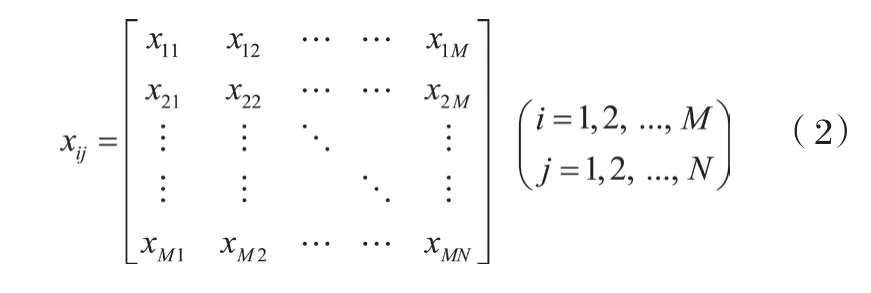
在式（2）中矩阵的每一行代表了每个传感器在做N次实验时所得到的数据,每一列代表子做一次实验时每个传感器的数据，融合时是将每一列的数据进行加权融合。则可以算出每个传感器的平均值及其标准差s。根据标准差s来对每个传感器分配权值。

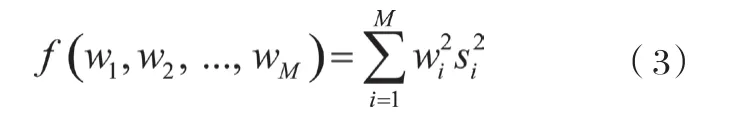
其中wi满足利用拉格朗日算法得出式（4）。

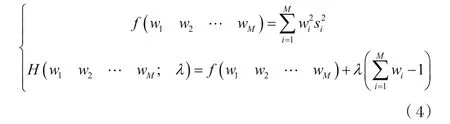
对式（4）求偏导数：

得到wi，则其融合后的数据就为：

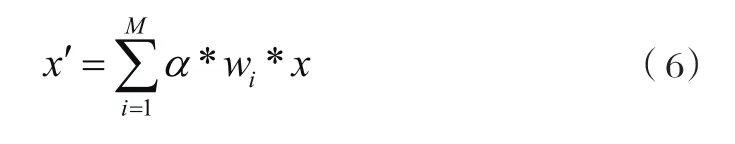
其中x是式（2）中每一列的数据。

3 实验应用

实验时采用剪切强度为90 kg/cm2，模拟可燃筒与弹头粘接情况制作了粘接面为24×20（mm）多传感器。检测时放置了6个传感器，对该试件做20次实验，其实验数据如表1，该试件的实际拉托为33.53千牛。

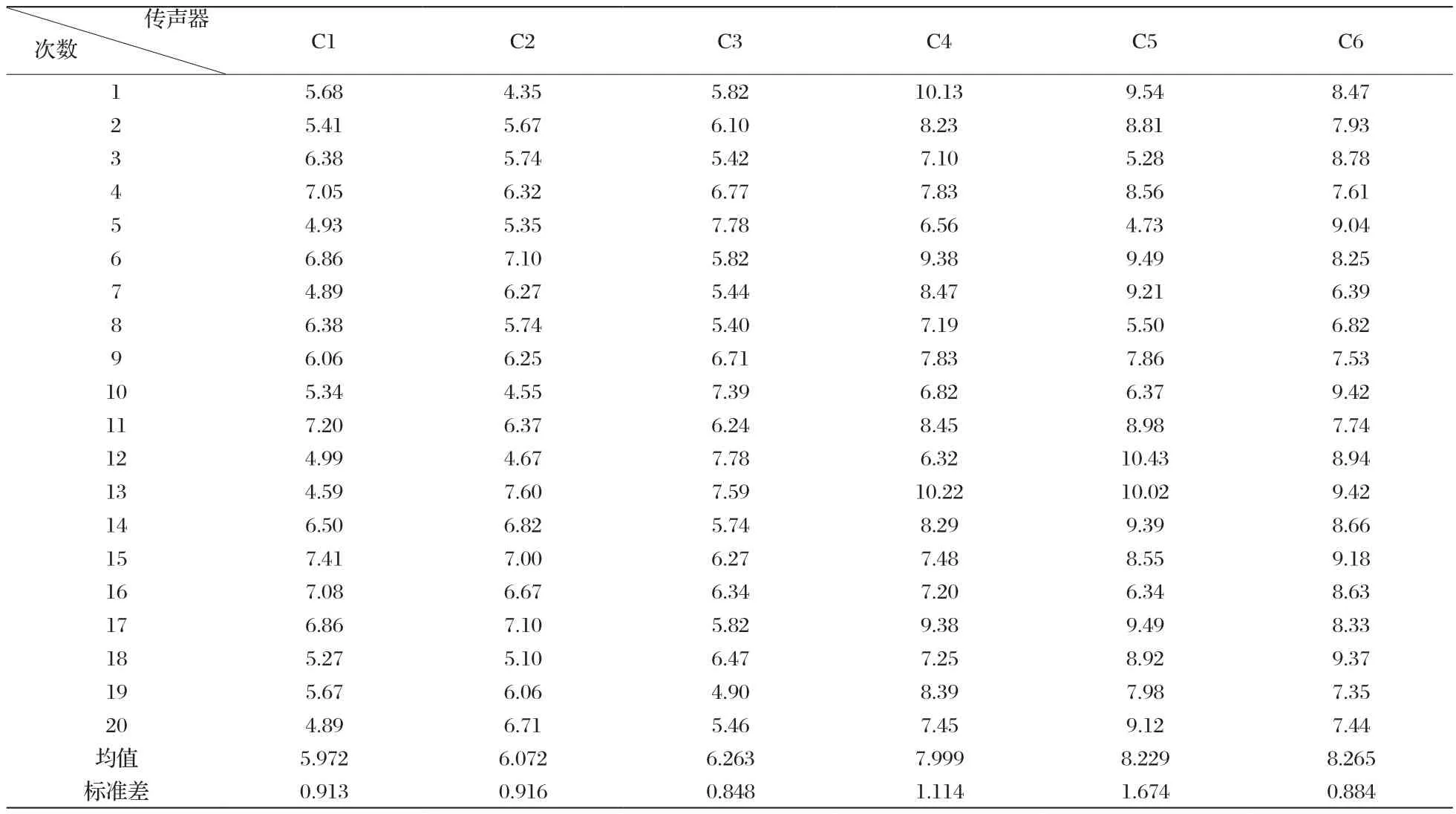
表1 试件的实验数据

根据公式（3）,（4）,（5）可求出6个传感器各自的权值。由式(6)求出20个融合数据（此时α=5）。

根据数理统计得到20个数据曲线近似符合图2所示。

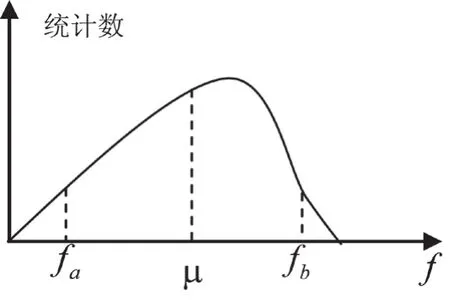
图2 近似曲线图

由此可以求出这些数据的均值μ及方差s2，若定融合错误率p=100%，即数据满足小于fa或者大于fb的力的个数分别与总数N比值。则可以预报该试件的拉托力范围为[32.63～38.16]。可以看出实际的拉托力在预报的范围之内。

4 结论

标准差反映了数据的离散程度，本文中所有的传感器给出的信息都是有用的，不能将其舍去。基于标准差加权融合算法在不知道传感器任何先验知识的情况下，得到多传感器融合估计数据。该融合算法简单且充分地利用了多传感器系统提供的信息，使拉托力更为准确，并为其拉托力范围的预测提供了很好的数据统计基础。

[1]宋冬利,李赫辆,李智超.接头形式对胶接强度的影响[J].辽宁工程技术大学学报,2000,19(4):426-429.

[2]黄漫国,樊尚春.多传感器数据融合技术研究进展[J].传感器与微系统,2010(3).

[3]黄惠宁,刘源璋.多传感器数据融合技术概述[J].科技信息,2010(15).

[4]邓自立,高媛.基于 Kalman 滤波的自回归滑动平均信号信息融合 Wiener 滤波器[J].控制理论与应用,2005,22(4):641-644.

[5]孙书利,崔平远.多传感器标量加权最优信息融合稳态Kalman 滤波器[J].控制与决策,2004,19(2):208-211.

[6]荣军,邱凯,黄世超.一种改进的联邦滤波算法及其应用研究[J].传感技术学报,2006,19(2):497-500.

[7]唐磊,赵春霞,唐振民,等.基于模糊自适应 Kalman滤波的GPS／DR数据融合[J].控制理论与应用,2007,24(6):891-894.

[8]杨风暴,韩炎.金属与非金属粘接质量的声阵列检测方法[J].华北工学院测试技术学报,2001,15(4).