钻孔应变差应变耦合系数反演与有关机理的探讨*

张晶刘琦

(中国地震局地震预测研究所，北京 100036)

钻孔应变差应变耦合系数反演与有关机理的探讨*

张晶刘琦

(中国地震局地震预测研究所，北京 100036)

研究反演分量式钻孔应变差应变耦合系数的方法，采用考虑方位角校正和相位滞后影响两种计算模型，计算结果显示大多数测站采用两种方法反演的耦合系数均比较相近，相位滞后、方位角校正以及拟合残差的结果相对稳定;但是有部分测站的差应变相位滞后偏离较大，从而导致采用两种方法反演的耦合系数差异较大。结合测站周边的构造分布，对可能导致该现象的物理机制进行了探讨。

钻孔应变;反演;差应变;耦合系数;相位滞后

1 引言

钻孔应变是研究地壳变形和应力场变化的重要手段，目前钻孔应变观测仪器主要分为体应变仪、分量应变仪。就分量应变仪来说，假设钻孔各观测分量的边界条件相同并忽略仪器系统误差的影响，如果观测分量为3个以上，就可以获得描述水平应变状态的主应变、主应变方向的动态变化，如果建立空间场的联系，则需要进行仪器的绝对标定。为减小仪器系统误差如测长基准杆本身长度变化、安装探头处地层温度变化等引起的漂移影响，目前国内采用四分量、八分量钻孔应变观测，可以做到仪器自检，与钻孔体应变观测相比，其优势是可通过组合获得差应变(剪应变)的变化，并通过面应变的自检减小系统误差的影响，即所谓分量钻孔应变的相对标定［1］。对钻孔应变组网观测，在一定程度上为研究形变波的时空传播特征、同震应变阶的分布特征，以及与空间场的动态变化建立一定的联系提供了可能性，因此对钻孔应变的绝对标定就显得尤为重要。

我国“十五”期间布设了一批YRY-4型四分量钻孔应变观测仪，四分量布置方式为“米”字形，即4个观测方向的径向位移传感器互成45°夹角，分别有两个正交方向，其和为面应变，其差为剪应变，剪应变变化与构造活动的关联可能更为密切。该观测网络自观测以来已连续几年获得了较为稳定的观测结果，本文在应变固体潮理论的基础上，对差应变有关参量的反演方法进行讨论，并对反演结果的可能机制进行分析探讨。

2 计算模型与方法

以四分量中接近南北向的观测方位角αx来建立坐标系xoy，其与正南北直角坐标系NoE的交角为αx，在坐标系xoy下，差应变Exx-Eyy为坐标系旋转45°后x'oy'坐标系下的剪应变(图1)，即

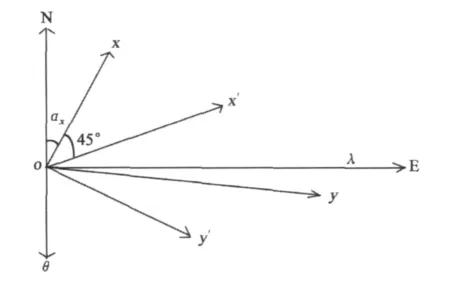
图1 坐标变换示意图Fig.1 Sketch of coordinate transformation

设eλλ、eθθ、eθλ分别为坐标系的东西、南北、剪切应变固体潮汐理论值，根据坐标旋转变换，将NoE坐标系旋转(αx+45°)后，可导出:

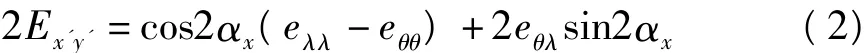
由式(1)可看出，式(2)为坐标系xoy下的差应变理论值，考虑观测中的仪器漂移项，分量式钻孔应变两个正交方向的差应变观测方程可表示为:

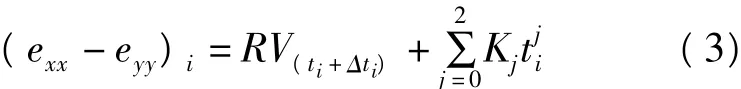
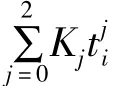
根据式(1)～(3)建立的观测模型，可以利用间接平差对一组差应变的时间序列进行反演，反演包括方位角改正δαx、时间滞后Δt、耦合系数R、常数项与飘移项系数K0、K1、K2共6个未知参数。这6个参数中方位角和时间滞后在某种意义上有一定的相关性，所以将方位角校正和时间滞后同时作为未知数会产生奇异解，因此分别取其一作为未知数、另一个作为已知数来求解。

方法1:如果将方位角校正作为未知数而不考虑时间滞后，由式(2)、(3)可导出:

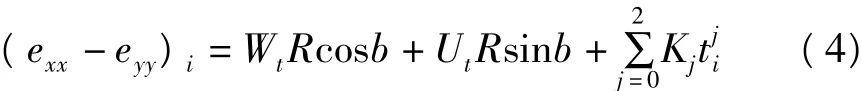
其中

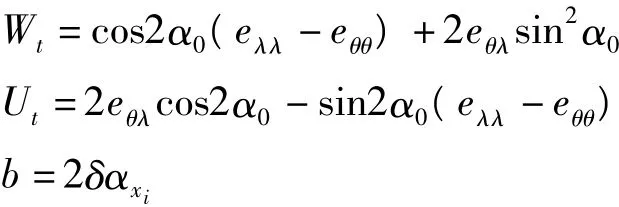
方法2:如果将时间滞后作为未知数而不考虑观测方位的误差，由式(2)、(3)可导出:

其中Δt为时间滞后，其他各参量同式(4)。

采用以上两种方法反演，均可得到耦合系数、漂移系数，并可分别获得方位角较正、时间滞后参数。

3 计算实例与分析

以江宁测站的四分量钻孔应变观测计算为例，江宁台井深50米，安山岩地层，岩芯完整无裂隙，2007年开始观测，自观测曲线稳定后两个面应变变化趋势基本一致，表明该台仪器的自检状况良好。采用该测站2009年1—12月的应变整时值观测数据，以2009年1月1日为起始时刻，对相对该时刻的应变增量进行分析计算。

表1、2分别为NE-NW、EW-NS两个差应变的计算结果，表中所列方法1、方法2为分别采用式(4)、式(5)计算的结果。图2为采用式(5)进行校正前后的差应变增量曲线，其变化量级在10-8以内。

图3为差应变观测值、改正值与理论值曲线，改正后的潮汐变化振幅与理论值更为接近，其中差应变EW-NS观测值与理论值相比相位滞后较大，按照相位滞后的时间将改正值曲线的时间提前，以接近理论值的相位(图3(b))。

从两个差应变的反演结果来看，NE-NW的结果明显好于EW-NS的结果，前者两种方法的耦合系数基本一致，方位角校正、时间滞后的变化都在较小的范围内(表1)，从观测与理论曲线的对比中也可看出其相位吻合得较好(图3(a))，说明在NE-NW方向的结果较为稳定;而EW-NS采用两种方法的耦合系数相差较大，方位角校正和时间滞后也较大，方位改正约30～40°，时间滞后平均为5.9小时(表2，图3(b))，超出了一般情况下所能预计的范围，在后面讨论其他测站的计算结果中，也表明这种现象并不是孤立的。

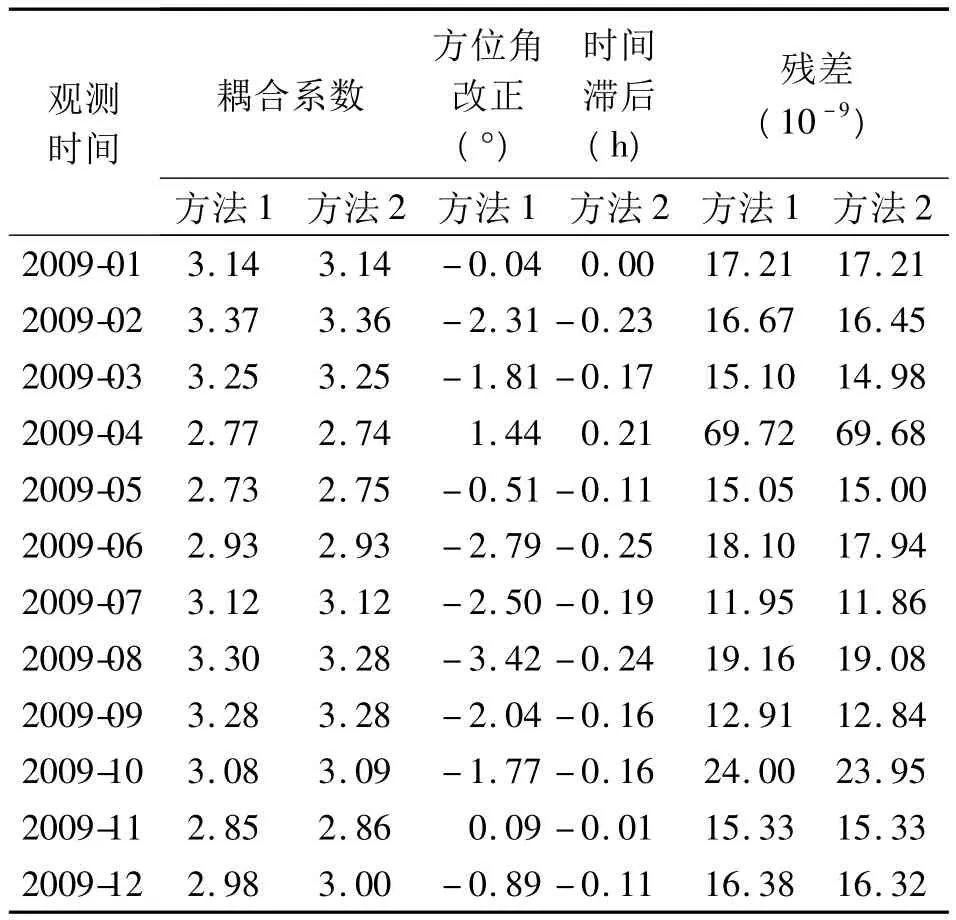
表1 差应变拟合参数(NE-NW)Tab.1 Fitting parameters of difference strain(NE-NW)

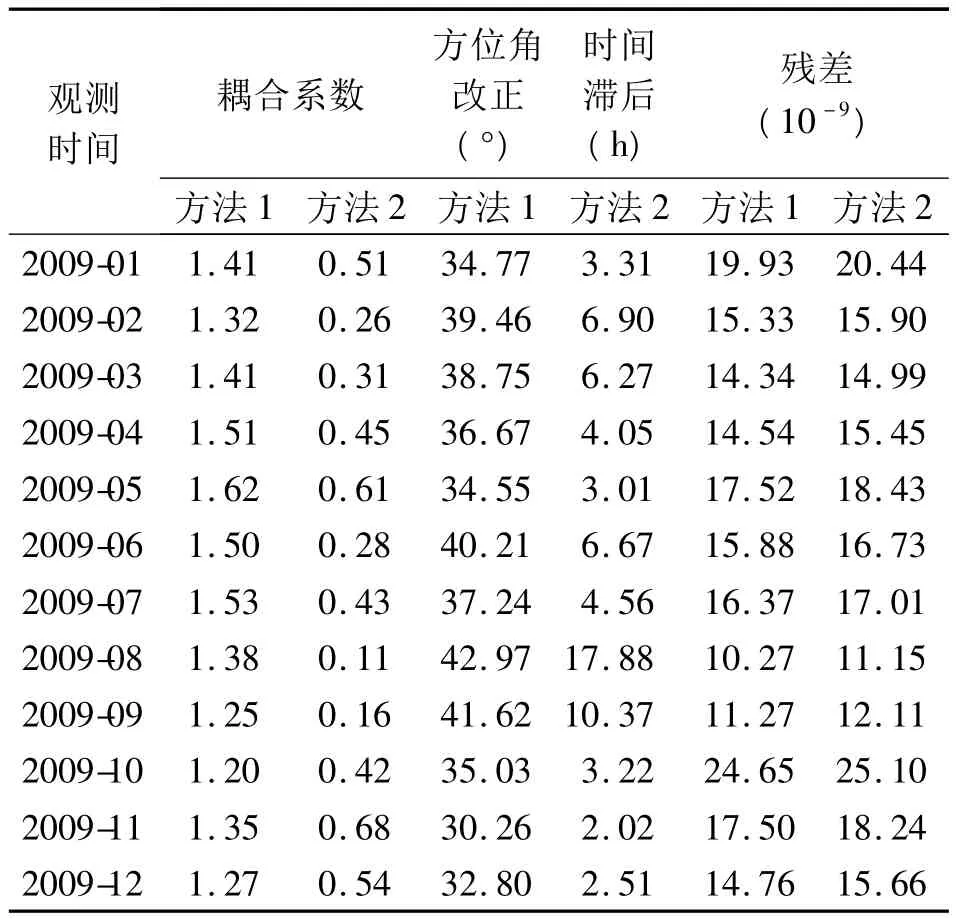
表2 差应变拟合参数(EW-NS)Tab.2 Fitting parameters of difference strain(EW-NS)

图2 校正前后的差应变观测增量曲线Fig.2 Incremental curves of difference strain observation before and after correction

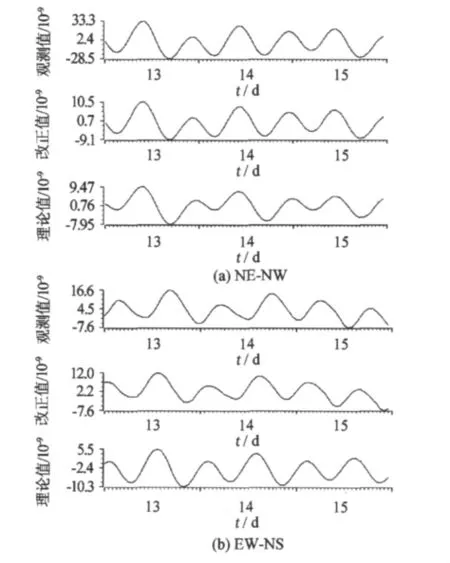
图3 差应变观测值、改正值与理论值Fig.3 Observation values，correction values and theoretical values of difference strain

采用上述方法对观测网络的40个测站中满足自检条件较好的25个台［2］进行计算，大部分测站的反演结果都比较稳定，方位角校正和相位滞后都较小，时间滞后平均在1小时以内;此外，25个测站中有7个测站的反演结果都出现了与江宁台类似的偏离现象，这里所指的偏差是同一个测站的两个差应变结果其中之一的偏差相对较大，而不同测站之间的绝对偏差由于所处地质构造背景、岩性的不同以及安装的具体条件不同而无法整体比较。

由图1和式(1)可知，差应变代表坐标系顺时针旋转45°坐标下的剪应变，可以认为EW-NS差应变代表了以NE、NW方向为轴的坐标系下的剪应变，照此方式将7个偏差较大的剪应变以及附近构造的情况列于表3，其中坐标轴方向是指反演偏差较大的剪应变的坐标轴方位角。

表3 剪应变坐标轴方向与测站附近断层走向Tab.3 Direction of coordinate axis of difference strain and strike of faults near observation stations

由于同一个平面坐标系下的两个剪应变相等，因此两个相互垂直的坐标轴可任选其一，并且EWNS与NE-NW两个差应变所对应的两个剪应变的坐标轴之间相差45°，因此如果剪应变的坐标轴方向与断层走向相差在22.5°以内，则可以认为比较接近。从表3所显示的结果来看，除了佘山台，其他台的剪应变轴方向与该测站周边的断层走向都很相近。此外，这7个测站的反演结果还存在一个共同的特点，即与另一个剪应变的结果相比，其耦合系数普遍偏小，拟合残差偏大，此时采用方法1反演的耦合系数其稳定性和一致性要好于采用方法2的反演结果。

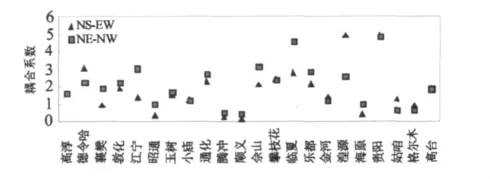
图4 差应变耦合系数反演结果Fig.4 Inversion results of coupling coefficients of difference strain

图4为其他部分测站采用方法1的差应变耦合系数反演结果，可以看出大部分的差应变标定系数都大于1，与面应变的耦合系数小于1的结果不同，钢筒的圆形截面使其截面的面积比较不易发生大小的变化，而钢筒的薄壁(几个毫米)则使其截面的形状易于变化［3］，这样的结果也是合理的。

4 小结与讨论

1)大多数测站采用两种方法计算的耦合系数都比较相近，相位滞后和拟合残差的结果相对稳定，但是有部分测站的差应变与理论值相比相位滞后较大，从而导致两种方法的耦合系数产生差异，此时采用方法2的耦合系数相对较小、拟合残差相对较大。因此在出现偏差较大的情况时，采用方法1的反演结果要好于方法2的。由于钻孔应变的绝对标定取决于面应变和差应变两部分的耦合系数，因此在进行钻孔应变绝对标定时，应该考虑有可能存在的这种偏差所带来的影响，尽管这种现象的成因还不十分清楚，但是其影响是客观存在的。

2)差应变观测结果与理论值偏离较大，其原因较为复杂，钻孔偏斜和探头安装误差等因素，以及钻孔周边介质的各向异性都可能对其产生影响。如果不考虑仪器安装等因素引起的偏差，从结果的分析来看，不能排除与附近构造有一定的关联，由于应变固体潮理论是建立在均匀介质且各向同性的假设前提下，因此观测结果的较大偏离可能反映了构造引起的介质各向异性的影响，而剪应变的这种差异与单分量相比则显得更加突出。尽管统计的样本目前还很有限，但可能为分析有关现象或研究其机理提供了一种思路与方法。

3)对可能导致其现象机理的讨论

国内外有关地震学研究学者利用地震定位的地壳介质剪切波分裂特征，研究应力和地壳介质的变化，获得了较为一致性的结论，即认为大多数台站的快剪切波偏振优势方向与主压应力方向或紧邻台站起控制作用的活动断裂走向一致［4-8］，地壳介质的各向异性主要是裂隙各向异性，剪切波穿过各向异性介质传播会发生分裂现象，剪切波分裂的偏振特性和时间延迟特性与裂隙介质的几何特性和物理性质有关，而且这种时间延迟与构造的距离有一定的关联，在距测站较近的台站收到这种影响较为明显［7，8］。研究地壳介质在引潮力作用下产生的周期性响应特征，也可能为我们研究介质各向异性以及应力场变化等问题提供新的途径与方法，在此方面已有研究学者利用分量钻孔应变观测数据研究介质的各向异性，获得了不同方向上潮汐因子各向异性的图像，认为潮汐振幅响应最大的方向与附近构造走向相近［9］，且潮汐振幅响应图像基本稳定。本文获取的潮汐剪应变响应特征，从现象上进一步证实了介质各向异性影响的存在，从而为今后进一步开展相关的理论研究，以及获取地震前后介质的变化提供了参考信息。

1 邱泽华，石耀霖，欧阳祖熙.四分量钻孔应变观测的实地相对标定［J］.大地测量与地球动力学，2005，(1):118-122.(Qiu Zehua，Shi Yaolin and Ouyang Zuxi.Relative in -situ calibration of 4-component borehole strain observation［J］.Journal of Geodesy and Geodynamics，2005，(1):118 -122)

2 刘琦，张晶.四分量钻孔应变资料的质量评价及拟合分析［J］.地震，2011，31(2):87-96.(Liu Qi and Zhang Jing.Quality evaluation and fitting analysis of 4-component borehole strainmeter data［J］.Earthquake，2011，31(2):87 -96)

3 邱泽华，石耀霖，欧阳祖熙.四分量钻孔应变观测的实地绝对标定［J］.地震，2005，25(3):27-34.(Qiu Zehua，Shi Yaolin and Ouyang Zuxi.Absolute calibration of 4-component borehole strainmeters［J］.Earthquake，2005，25 (3):27-34)

4 Gao Y，et al.Shear-wave splitting in the southeast of Cathaysia block，South China［J］.Seismol，2009，13:267-275.

5 Gao Y and Crampin S.Shear-wave splitting and earthquake forecasting［J］.Terra Nova，2008，20(6):440-448.doi:10.1111/j.1365-3121.2008.00836.x

6 赵博，高原，石玉涛.张家口-渤海地震带与山西地震带交汇区的地壳剪切波分裂［J］.地球物理学报，2011，54 (6):1 517-1 527.(Zhao Bo，Gao Yuan and Shi Yutao.Shear wave splitting in the crust in the intersection zone of the Zhangjiakou-Bohai seismic belt with the Shanxi seismic belt［J］.Chinese J Geophys，2011，54(6):1 517-1 527)

7 Gao Yuan and Stuart Crampin.A stress-forecast earthquake (with hindsight)，where migration of source earthquakes causes anomalies in shear-wave polarizations［J］.Tectonophysics，2006，426:253-262.

8 Elizabeth S Cochran，Li Yonggang and John E Vidale.Anisotropy in shallow crust observed around the San Andreas fault before and after the 2004 M6.0 Parkfield earthquake［J］.Bulletin of the Seismological Society of America，2006，96(4B):S364-S375.

9 池顺良，武红岭，骆鸣津.钻孔应变观测中潮汐因子离散性与各向异性原因探讨——“十五”数字地震观测网络分量钻孔应变仪首批观测资料分析解释［J］.地球物理学进展，2007，22(6):1 746-1 753.(Chi Shunliang，Wu Hongling and Luo Mingjing.Discussion on strain tidal factor separation and anisotropy——Analysis of first data of borehole component strain-meter of China’s digital seismological observational networks［J］.Progress in Geophysics，2007，22 (6):1 746-1 753)

COUPLING COEFFICIENTS INVERSION OF DIFFERENCE STRAIN IN BOREHOLE OBSERVATION AND DISCUSSION OF RELATED MECHANISM

Zhang Jing and Liu Qi
(Institute of Earthquake Science，CEA，Beijing 100036)

The method of coupling coefficients inversion for 4-component borehole strainmeters was studied，which adopts two computation models including azimuth correction and phase lag effect.Using the data from the network of 4-component borehole strain observation during the Tenth Five-Year Project of China，the calculation results show that coupling coefficients inverted with the two models are close to each other in most sites，and the results of phase lag，azimuth correction and simulation residual are relatively stable.However，some sites’results of phase lag are different obviously，which results in great difference between coupling coefficients inverted with the two models.On the basis of faults distribution of sites’surroundings，the physical mechanisms that possibly lead to the difference are discussed.

borehole strain;inversion;difference strain;coupling coefficients;phase lag

1671-5942(2012)02-0155-05

2011-10-23

中国地震局地震行业科研专项(201108009)

张晶，女，研究员，主要从事地壳形变与地震预测应用研究.E-mail:zhangjing@seis.ac.cn

P315.72+5

A