航空重力测量水平加速度改正的小波预处理*

田颜锋 李姗姗 肖 凡

航空重力测量水平加速度改正的小波预处理*

田颜锋1)李姗姗2)肖 凡3)

根据航空重力测量中水平加速度改正的频谱特性和小波变换频带划分规则，导出了水平加速度改正的小波预滤波尺度。以实测数据为例，基于信号小波变换尺度间的相关性，分别利用Haar小波、db4小波、db6小波和sym6小波对其进行小波预滤波处理，并与目前常用的FIR低通预滤波处理结果进行比对，结果表明:小波预滤波处理水平加速度改正的精度较FIR低通预滤波处理得到的精度高，并且用db系列小波进行预处理得到的结果精度更加均匀，据此提出对水平加速度改正预处理时应选用db系列小波或者支集较长的sym8小波。

航空重力测量;预滤波;水平加速度改正;厄特弗斯改正;傅里叶变换;小波变换

1 引言

我国的航空重力测量系统CHAGS(Chinese Airborne Gravity System)采用基于稳定平台的航空重力仪，稳定平台维持其传感器的垂直指向［1］。当稳定平台保持当地水平时，重力仪指向当地铅垂线方向，重力测量不受水平加速度的影响;当稳定平台不能保持当地水平时，重力测量受到飞行载体水平加速度的影响从而产生水平加速度改正。它是航空重力测量数据处理中必不可少的环节，由于改正模型中二次项的出现，改变了整个模型的线性特征，因此必须对原始数据进行预滤波处理。石磐［2］利用FIR低通滤波器对水平加速度改正进行预滤波处理，估算出其平均量级约为3×10-5ms-2;孙中苗［3］论证了计算水平加速度改正的两步法和一步法之间的关系，根据平台倾角的频谱特性提出水平加速度改正的基本滤波尺度为10 s，利用该尺度得到的重力测量结果与地面向上延拓参考值之间的系统差优于0.5×10-5ms-2。但是FIR滤波器不能有效抑制混入信号频带内部的噪声分量，由此，本文将基于航空重力测量减震系统得到水平加速度改正的小波预处理尺度，并对其进行小波处理。

2 小波变换的基本原理

小波被定义为积分为零且平方可积的函数，满足［4-7］

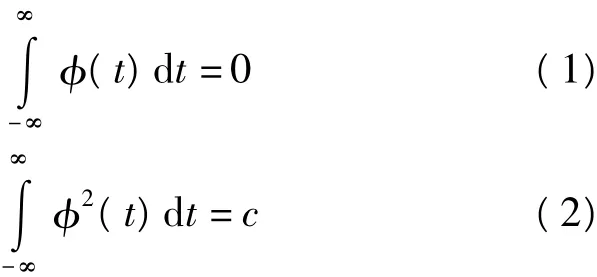
的函数φ(t)就被称为基小波，由基小波可以派生一个小波函数簇

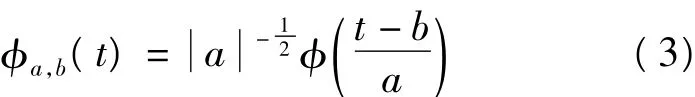
式中a表示膨胀系数，b表示平移参数。在这个小波基上将函数f(t)分解即可得到该序列的连续小波变换

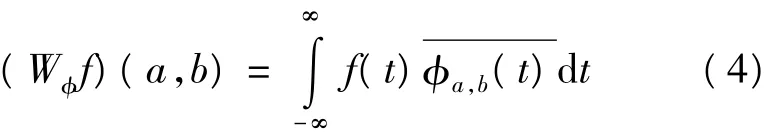
3 水平加速度改正的小波预处理

3.1 水平加速度改正的计算模型

计算水平加速度改正有两种基本方法:两步法和一步法。两步法先计算稳定平台的倾角，再计算水平加速度改正，其数学模型为［4］:

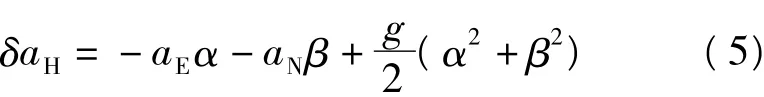
其中α和β为平台倾角，aE和aN分别是飞机的东向、北向水平加速度，可由机载GPS导出，g为测得的重力值。

一步法假设稳定平台的水平轴严格垂直，令fx和fy分别为平台横轴和纵轴方向的水平加速度，则有［8］

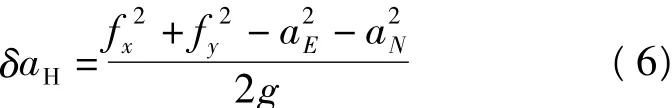
文献［9］推导出这两种方法在理论上等价。

由于式(6)中平方项的存在，产生的系统误差具有非线性特性，这加大了分析加速度谱的难度。需同时分析航空重力测量厄特弗斯改正［2］

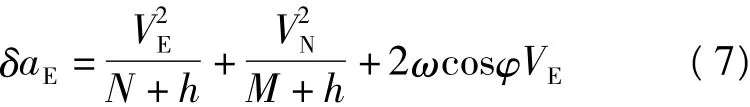
式中VE、VN分别是水平速度的东向分量和北向分量，M、N是所在位置子午圈和卯酉圈曲率半径，h是飞机航高，ω是地球自转角速度，φ是航点纬度。分析式(6)和式(7)都含有平方项，但是数据处理中不同尺度的预滤波处理对水平加速度影响较大，而厄特弗斯改正基本不受预滤波的影响。进一步研究水平加速度改正的计算模型发现:式(6)中所涉及的数据不仅包含原始观测量fx和fy，也含有计算得到的载体加速度aE和aN，因此可以初步确定计算载体加速度时会引起数据频谱中噪声成分的增加。图1的实测数据分析也证实了这个结论:速度的能量基本集中在频谱图的低频部分，加速度的能量中含有大量频谱集中在0.01 Hz附近的噪声。

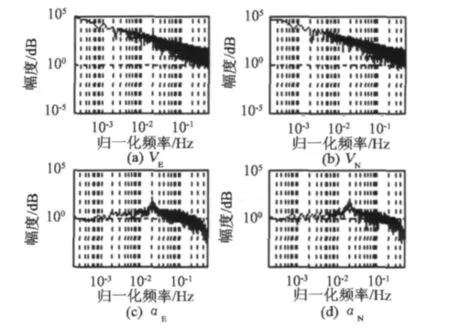
图1 载体速度分量和水平加速度分量的频谱图Fig.1 Spectrum diagram of the carrier’s velocity constituent and horizontal acceleration constituent

3.2 小波变换尺度的确定

预滤波的最佳尺度存在各种假定，较常见的一种假定是认为预滤波的尺度与最终滤波器的尺度相近时最佳，由经验可知，航空重力数据滤波处理时采用的滤波器时域周期为100 s或者更高［9］，但通过实验发现，采用时域周期为50 s的低通滤波器进行预滤波时输出的加速度分量已经全部接近零，因此采用过长的低通滤波器进行滤波将滤掉加速度信息的有效部分，可见利用最终的滤波器进行预滤波处理是不可行的。

考虑到航空重力测量系统的构成，水平加速度计和测姿装置固定在稳定平台内部，稳定平台通过专门的减震系统悬浮在框架之间［10］。保护稳定平台的减震系统由减震绳和8个油压减震器构成，系统外部的高频噪声能否传递到稳定平台内部在很大程度上取决于减震系统的性能。出于技术保密的需要，Lamp;R公司并未公布其产品的减震系统性能，我们只能通过相关数据的频谱特性来估计减震系统的减震效果。稳定平台内部固定有水平加速度计和姿态测定装置，选取记录的内部水平加速度数据来分析减震系统的性能。令fx表示平台横轴加速度计敏感到的横向水平加速度，fy表示平台纵轴加速度计敏感到的纵向水平加速度，对某测区所有测线的fx和fy分量进行频谱分析，结果如图2所示，稳定平台内部加速度计测得的水平加速度频谱基本都在0～0.1 Hz之间，据此建议该航空重力测量系统应选定10 s的预滤波尺度。

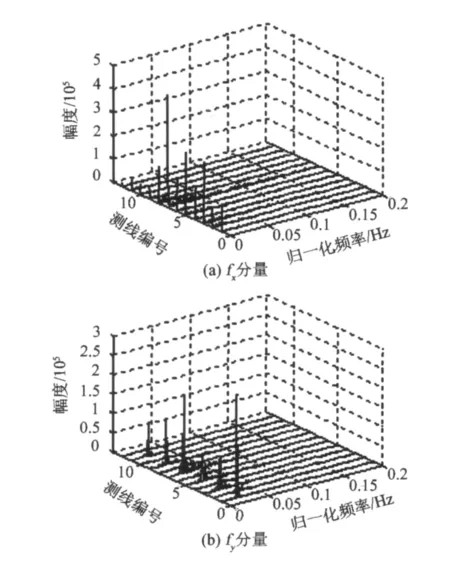
图2 试验区域所有测线横向加速度分量的频谱图Fig.2 Spectrum diagram of horizontal acceleration component of all flight path in the test area

稳定平台的两根水平轴互相垂直，加速度计敏感到的水平加速度fx和fy与GPS测量所得的载体水平加速度aE和aN存在如下关系［8］

其中α、β表示稳定平台的倾角。从式(8)可以看出:平台敏感到的水平加速度fx和fy是载体水平加速度aE和aN的线性组合，根据傅里叶变换的性质，fx和fy的频谱也是载体水平加速度aE和aN频谱的线性组合，即:在理论上fx、fy、aE和aN具有相同的频谱构成，由此可以确定aE、aN、fx和fy的预滤波尺度相同。

根据小波分析的思想，如果采集得到的是频率范围为［0，Ω］的信号，那么对该信号进行一次小波分解可以将原信号分成低频部分和高频部分，它们的频率范围分别为［0，Ω/2］、［Ω/2，Ω］。再次对低频部分进行分解，可以得到频带在［0，Ω/4］、［Ω/4，Ω/2］中的两个信号，以此类推可以将信号不停地分解至最顶层。当然，也可以采用小波包的方法对信号的高频部分进行同样的分解，这样就可以完成滤波和去噪的工作［11］。航空重力测量观测数据的采样间隔是1 s，对应的小波分析频率为0.5 Hz，进行三层的小波变换基本符合水平加速度改正的频率要求。

3.3 水平加速度改正的小波预处理

小波滤波方法对噪声的性质有3个基本假设［12］:一是噪声均匀低分布在所有系数中;二是数据中的噪声部分经过小波变换后大多数为零或者近似为零;三是噪声水平不能太高。航空重力测量中的噪声可以看做随机的Gauss白噪声，符合第一个条件。载体的加速度分量aE小波分解提取后如图3所示。

从图3可以看出，原始数据经小波变换后的细节部分基本为0。结合图1和图2，数据的噪声水平不高，符合小波滤波方法对噪声的3个基本假设。因此可以利用小波滤波方法对加速度数据进行滤波处理。

选取Harr小波、db4小波、db6小波和sym4小波对水平加速度改正进行预滤波处理，它们的函数如图4所示。

为验证水平加速度改正的小波滤波处理效果，对某地区航空重力测量数据进行处理分析。该测区属陆海交界区域，载体平均飞行速度为60 ms-1，航高约500 m，运载平台为国产航测机。考虑到目前航空重力测量数据滤波处理普遍采用FIR低通滤波器，故此处计算不同预滤波尺度下该测区某条测线水平加速度改正后将其结果与10 s预滤波结果进行对比分析。图5展示了不同尺度预滤波处理对水平加速度改正最终滤波结果的影响，从图5可以看出，水平加速度改正经小波预滤波处理后的最终结果与FIR预处理的精度相当。表1列出不同方法处理了某条测线对最终结果影响的数据统计特性。

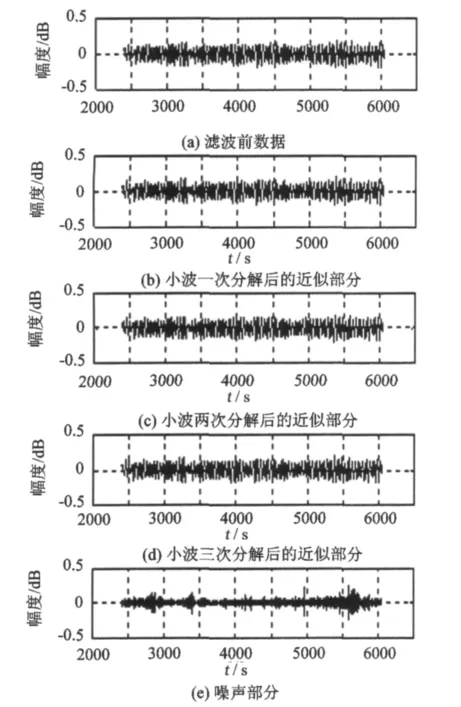
图3 水平加速度分量aE的db4小波分解Fig.3 db4 wavelet decomposition of the horizontal acceleration component aE

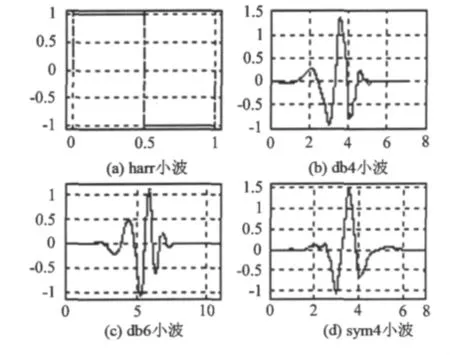
图4 本文选取的小波函数Fig.4 Wavelet functions chosen in this article

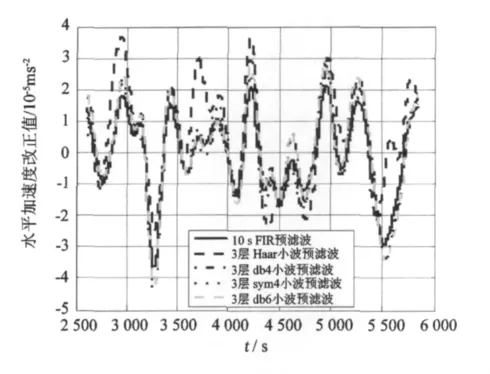
图5 不同小波预滤波对水平加速度改正最终结果的影响Fig.5 The influence of the different wavelets pre-filters to the final results of the horizontal acceleration correction

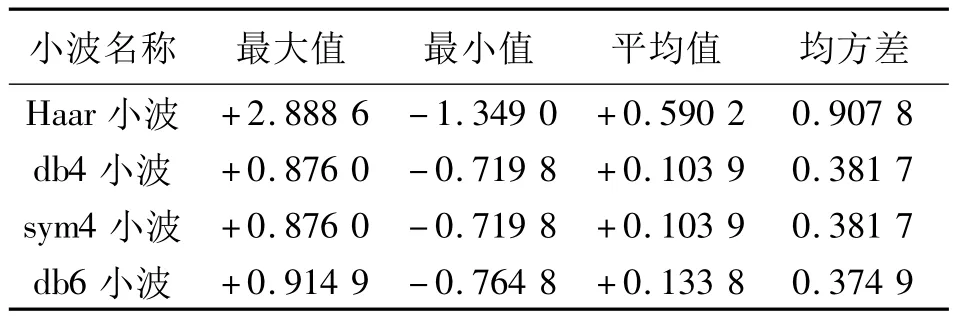
表1 与10 s FIR预滤波相比，小波预滤波对最终结果影响的数据统计特性(单位：10-5ms-2)Tab.1 Statistic characteristic of the wavelet pre-filter impact on the final results compared with 10 s FIR pre-filter(unit：10-5ms-2)

3.4 精度评定

从表1可以看出，水平加速度改正经小波滤波和FIR低通滤波预处理后的差值小于 1×10-5ms-2。由于航空重力测量中加速度改正的真值无法确定，因此无法从表1判断出各滤波方法的优劣。选取四种方法中的任一个预滤波结果作为真值，再加入均值为零、方差为0.02的Gauss白噪声，分别用FIR低通滤波和不同的小波对其进行滤波处理，并与不加噪声的数据进行对比，其终结果如表2。

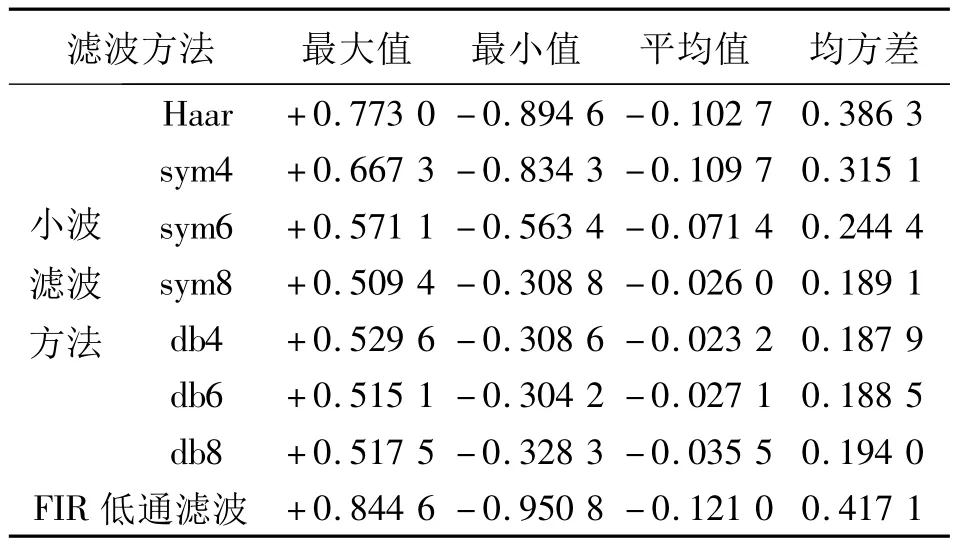
表2 不同预滤波方法对最终结果的影响(单位：10-5ms-2)Tab.2 Influence of different wavelet pre-filter on the final results(unit：10-5ms-2)

从表2可以看出，与FIR低通预滤波相比，小波预滤波的精度有不同程度的提高，特别是sym8小波和db小波簇更是将水平加速度改正的误差控制在0.2×10-5ms-2内。遗憾的是航空重力测量数据的信噪比低，目前尚未找到行之有效的小波滤波方法，因此将小波滤波用于最终的滤波处理还需进一步的研究。

4 结论

传统的FIR低通滤波首先用Fourier变换将信号变换到频域，然后再进行低通滤波处理。当信号的有效频谱中混有噪声时，FIR的滤波效果较差，因此FIR低通滤波器不能抑制混入信号频带内部的噪声分量。采用Haar小波、db小波簇和sym小波簇对水平加速度改正进行预滤波处理，可以得出:1)小波变换能够抑制混入有效频带范围内的噪声，进一步提高了数据处理的精度;2)小波变换实现简单，对边界数据的影响较小。表2的精度分析表明，在不产生边界问题的前提下，sym8小波和 Daubechies小波簇精度最高，适用于水平加速度改正的预滤波处理。

1 孙中苗.航空重力测量理论、方法及应用［D］.郑州:信息工程大学测绘学院，2004.(Sun Zhongmiao.Theory，methods and application of airborne gravimetry［D］.Zhengzhou: Institute of Surveying and Mapping，2004)

2 石磐，孙中苗，肖云.航空重力测量中水平加速度改正的计算与频域分析［J］.武汉大学学报(信息科学版)，2001，26(6):549-553.(Shi Pan，Sun Zhongmiao and Xiao Yun.Calculation and spectra analysis of horizontal acceleration correction(HACC)for airborne gravity［J］.Geomatics and Information Science of Wuhan University，2001，26(6): 549-553)

3 孙中苗，等.Lamp;R航空重力仪的水平加速度改正［J］.测绘科学技术学报，2007，24(4):259-262.(Sun Zhongmiao，et al.Horizontal acceleration correction for the airborne gravity［J］.Journal of Geomatics Science and Technology，2007，24(4):259-262)

4 Donald B P and Andrew T W.Wavelet methods for time series analysis［M］.Cambridge:Cambridge University Publishing Company，2006.

5 高成.Matlab小波分析与应用(第2版)［M］.北京:国防工业出版社，2007.(Gao Cheng.Wavelet analysis and its application(2nd)［M］.Beijing:National Defence Industry Press，2007)

6 耿则勋.小波变换理论及在遥感影像压缩中的应用［M］.北京:测绘出版社，2002.(Gen Zexun.Wavelet transform and its application in image compression of remote sensing［M］.Beijing:Surveying and Mapping Publication，2002)

7 孙延奎.小波分析及其应用［M］.北京:机械工业出版社，2005.(Sun Yankui.Wavelet analysis and its application［M］.Beijing:Machine Industry Press，2005)

8 Peters M F and Brozena J M.Methods to improve existing shipboard gravimeters for airborne gravimetry［A］.Presented at IAG Symposium on Airborne Gravity Field Determination［C］.Boulder，Colorado，1995，39-45.

9 孙中苗，等.航空重力测量数据的滤波与处理［J］.地球物理学进展，2004，19(1):119-124.(Sun Zhongmiao，et al.Filtering and processing for the airborne gravity data［J］.Progress in Geophysics，2004，19(1):119-124)

10 LaCosteamp;Romberg Company.Model“S”air-sea dynamic gravity meter system II instruction manual［S］.Texas: LRC，2003.

11 程正兴.小波分析与应用实例［M］.西安:西安交通大学出版社，2006.(Cheng Zhengxing.Examples of wavelet analysis and its application［M］.Xi’an:Xi’an Traffic University Press，2006)

12 潘泉，等.小波滤波方法及应用［M］.北京:清华大学出版社，2005.(Pan Quan，et al.Wavelet filtering method and its application［M］.Beijing:Tsinghua University Press，2005)

WAVELET PRE-PROCESSING FOR HORIZONTAL ACCELERATION OF AERIAL GRAVITY MEASUREMENT

Tian Yanfeng1)，Li Shanshan2)and Xiao Fan3)

(1)PLA 73603 Troops，Nanjing 210049 2)Institute of Surveying and Mapping，Information Engineering University，Zhengzhou 450052 3)PLA 61365 Troops，Tianjin 300140)

According to the spectrum characteristic of the horizontal acceleration correction in the aerial gravity measurement and the partition rules of wavelet transformation frequency band，the wavelet pre-filter scale of the horizontal acceleration correction is deduced.On the basis of the correlation among the wavelet transform scales of the signal，as an example，some surveying data were pre-processed by Haar wavelet、db4 wavelet、db6 wavelet and sym6 wavelet，and the results are compared with the results from FIR low pass filter in common use.The comparison shows that the precision of the wavelet pre-filter is higher than the FIR low pass filter in the pre-processing of the horizontal acceleration correction and it is more symmetrical as pre-processed by db serial wavelets.Thus it is proposed that the Daubechies wavelets or the sym8 wavelet with much longer branch are more useful in the pre-processing of the horizontal acceleration correction.

aerial gravity measurement;pre-filter;horizontal acceleration correction;Eötvös correction;Fourier transform;wavelet transform

(1)解放军73603部队，南京 210049 2)解放军信息工程大学测绘学院，郑州 450052 3)解放军61365部队，天津300140)

1671-5942(2012)02-0115-05

2011-12-04

田颜锋，男，1981年生，硕士，主要研究方向为物理大地测量.E-mail:yanftian@126.com

A